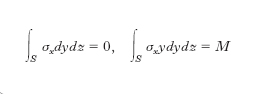flessione

Anatomia

Movimento di un’articolazione per il quale l’estremità distale di un segmento corporeo si avvicina a quella prossimale del segmento corporeo contiguo. Muscolo flessore è il muscolo che ha per azione principale il movimento di f.: si tende a distinguere il singolo muscolo flessore dai muscoli congeneri, indicando nel nome la sede della massa muscolare (superficiale delle dita; profondo delle dita), o di una delle sue inserzioni (radiale del carpo; ulnare del carpo), oppure la sua conformazione (lungo dell’alluce; breve dell’alluce), o la destinazione a uno o più organi (comune delle dita; proprio del pollice).

Linguistica

Processo per cui, nelle lingue flessive, come le indoeuropee e le semitiche, una parola, per mutamento del tema e della radice (➔ apofonia) ovvero per aggiunzione e fusione al tema di suffissi, può esprimere valori e rapporti grammaticali diversi: si distingue in f. verbale, o coniugazione dei verbi, f. nominale, o declinazione dei sostantivi e degli aggettivi, e f. pronominale, o declinazione dei pronomi.

Tecnica

Nella scienza delle costruzioni, sollecitazione che si verifica in una trave ad asse rettilineo o ad asse curvilineo piano di non elevata curvatura, quando ogni sua sezione trasversale è soggetta a momento flettente.

F. semplice

fig. A

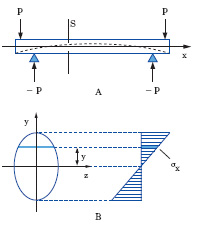
La f. si dice semplice quando ogni sezione trasversale della trave è soggetta soltanto a momento flettente. È questo, per es., per il tratto compreso fra i due appoggi (fig. A), il caso di una trave orizzontale con due sbalzi uguali che portano agli estremi due pesi P, agenti in un piano che contenga l’asse della trave. Il momento flettente è costante in tutte le sezioni della trave comprese tra gli appoggi; se la trave è rettilinea, di sezione costante e simmetrica rispetto al piano di sollecitazione, si nota che, nel moto di deformazione conseguente all’applicazione dei pesi, l’asse geometrico tra gli appoggi si trasforma in un arco di circonferenza (punteggiato in fig.). Il conseguente allungamento delle fibre longitudinali è variabile lungo l’altezza della trave; alcune fibre si allungano e altre si accorciano e si ha, in ogni piano parallelo al piano di sollecitazione, una fibra intermedia che conserva lunghezza invariata, detta fibra neutra. L’insieme delle fibre neutre costituisce lo strato neutro, l’intersezione di questo con ciascuna sezione trasversale è l’asse neutro della sezione. L’ipotesi avanzata da G. Bernoulli che nella deformazione della trave la generica sezione trasversale si conservi piana è convalidata dalla teoria dell’elasticità, e corrisponde ad ammettere la proporzionalità tra gli allungamenti delle varie fibre longitudinali e la loro distanza dalla fibra neutra. Se nella generica sezione trasversale S (ellittica in fig. B) si assumono per riferimento l’asse di sollecitazione (intersezione tra il piano di sollecitazione e il piano della sezione) come asse y e l’asse neutro (ortogonale al primo per la supposta simmetria) come asse z, le condizioni di equilibrio si esprimono con le due equazioni:

dove σ_x è la tensione normale nel generico elemento superficiale di S, distante y dall’asse neutro, e M il momento flettente nella sezione medesima. Queste equazioni, tenendo conto dell’ipotesi di Bernoulli e della legge di Hooke, consentono di riconoscere che l’asse neutro coincide con l’asse baricentrale ortogonale all’asse di sollecitazione, e che σ_x è espressa dalla formula σ_x = My/I, con I momento d’inerzia della S rispetto all’asse neutro. Cioè (fig. B) la tensione normale ha andamento lineare nell’altezza della trave: si annulla sull’asse neutro, su un lembo della sezione raggiunge il valore massimo (di compressione) e sul lembo opposto il valore minimo (negativo), cioè il massimo valore dello sforzo di trazione. Nel caso più generale che la trave abbia sezione di forma qualsiasi, valgono gli stessi risultati se l’asse di sollecitazione coincide con uno degli assi principali d’inerzia della S; altrimenti, l’asse neutro non è più ortogonale all’asse di sollecitazione, ma ne è il diametro coniugato rispetto all’ellisse centrale d’inerzia della S: in tal caso la f. si dice deviata, e si ha σ_n=M s senδ/I_n, con s distanza del generico elemento d’area dall’asse neutro, I_n momento d’inerzia della S rispetto al medesimo, e δ angolo formato dall’asse neutro con l’asse di sollecitazione. I risultati della teoria della f. sono in generale in accordo con l’esperienza, ma se ne discostano, anche sensibilmente, quando non possa ammettersi la legge di Hooke: è quanto avviene, per es., per tutti i materiali ferrosi sollecitati oltre il limite di proporzionalità e per tutti i calcestruzzi cementizi in condizioni di sollecitazione prossime alla rottura.

F. e taglio

La sollecitazione di f. è generalmente accompagnata dalla sollecitazione di taglio: è tale, per es., in genere, il caso di una trave rettilinea soggetta a forze incidenti normalmente all’asse della trave. Sforzo di taglio e momento flettente nella generica sezione S si ottengono allora rispettivamente dalla somma algebrica delle forze esterne (carichi e reazioni vincolari) che precedono o che seguono la sezione, rapportate all’area di questa, e dalla somma algebrica di corrispondenti momenti rispetto al baricentro della S. Non è più rigorosamente verificata l’ipotesi di conservazione delle sezioni piane, ma gli scostamenti da essa sono normalmente tanto piccoli da poter essere trascurati. La distribuzione degli sforzi interni si ha dalla sovrapposizione degli effetti delle due sollecitazioni semplici di f. e di taglio; in ogni punto dell’asse neutro di S è massima la tensione tangenziale di taglio. La legge di variazione delle tensioni tangenziali τ nella sezione trasversale resta espressa dalla relazione τ=TS′/Iz, essendo T lo sforzo di taglio, I il momento d’inerzia della sezione rispetto all’asse neutro, z la larghezza della sezione nel punto ove si vuole la τ e S′ il momento statico rispetto all’asse neutro della parte di sezione sovrastante la fibra stessa. Quanto alla tensione normale, essa si annulla, sull’asse neutro, solo in direzione perpendicolare alla S, ed è diversa da zero nelle altre direzioni parallele al piano xy, raggiungendo un massimo (compressione) e un minimo (trazione) in corrispondenza a due di tali direzioni tra loro ortogonali (➔ Mohr, Christian Otto).

F. e torsione

La f. può essere accompagnata da torsione. Un caso di particolare importanza è quello di un cilindro circolare retto, soggetto nella generica sezione trasversale S sia a momento flettente, sia a momento torcente: nei due punti del perimetro della S appartenenti al piano di sollecitazione della f., si ha il massimo valore della tensione normale (provocata dal momento flettente) e il massimo della tensione tangenziale (per effetto del momento torcente).