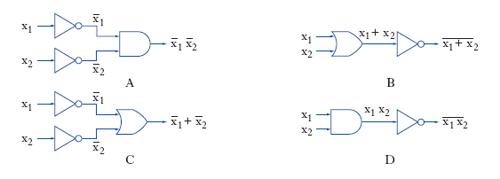logici, circuiti
In elettronica, dispositivi che attuano operazioni di algebra logica binaria.
Operazioni logiche binarie
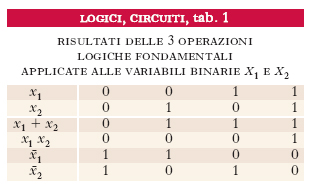
Per la schematizzazione di circuiti l. elettronici, detti circuiti di commutazione, e per la determinazione delle relazioni funzionali ottenibili per mezzo di essi, sono normalmente utilizzate la formulazione dell’algebra logica e le notazioni proposte da G. Boole (algebra booleana; ➔ Boole, George), non solo per la semplicità ma soprattutto perché tutte e sole le operazioni definite da Boole sono applicabili ai circuiti di commutazione. Indicando con 0 (assenza) e 1 (presenza) i due valori possibili delle variabili binarie, si definisce somma logica (operazione OR) di due o più variabili indipendenti xi l’operazione il cui risultato è una variabile binaria che assume il valore 0 se e solo se tutte le xi hanno il valore 0; si definisce prodotto logico (operazione AND) l’operazione il cui risultato vale 1 se e solo se tutte le xi hanno il valore 1; infine, inversione o negazione (operazione NOT) della variabile x è l’operazione il cui risultato dà il valore alternativo di x. Indicheremo con x1+x2, x1∙x2 (o anche x1 x2), x̄ rispettivamente la somma logica, il prodotto logico e l’inversione. In tab. 1 sono riportati i risultati delle 3 operazioni logiche fondamentali applicate alle variabili binarie x1 e x2; valgono le relazioni:
x + 0 = x; x + 1 = 1; x + x = x; x + x̄ = 1;
x ∙ 0 = 0; x ∙ 1 = x; x ∙ x = x; x ∙ x̄ = 0.
Una funzione logica di n variabili indipendenti può essere definita mediante una relazione analitica nella quale alle n variabili sono applicate in vario modo le operazioni fondamentali di somma logica, prodotto logico e inversione; il numero di funzioni logiche diverse di n variabili è uguale a 22n (disposizioni con ripetizione degli elementi 0 e 1). In tab. 2 sono riportate le configurazioni delle 16 funzioni logiche diverse ottenibili con due variabili binarie, in corrispondenza ai valori assunti da queste. Dal confronto con la tab. 1 si riconosce, per es., che la funzione f3 è l’inversione di x1 (f3=x̄1). Le funzioni f1=x̄1x̄2=−−x1+x2−−−, detta prima funzione di Sheffer o operazione NOR (inversione dell’operazione somma) e f7=x̄1+x̄2=−−x1x2−−−, detta seconda funzione di Sheffer o operazione NAND (inversione dell’operazione prodotto), sono importanti in quanto è possibile effettuare qualunque operazione logica usando esclusivamente l’una o l’altra di esse; la funzione f6=x̄1x2+x1x̄2, detta funzione di non equivalenza o operazione OR esclusivo (XOR), assume valore 1 solo se le due variabili binarie hanno valore diverso tra loro. Quanto sopra può essere esteso al caso di più variabili binarie. Le tabelle 1 e 2 sono dette anche tavole di verità delle operazioni logiche che in esse compaiono.
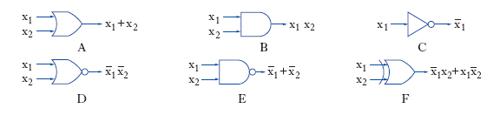
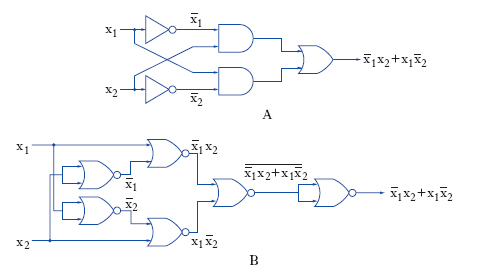
Ciascuno dei circuiti digitali impiegati per realizzare una delle 3 operazioni logiche fondamentali è chiamato operatore logico elementare o porta (gate); si hanno di conseguenza: l’operatore elementare di somma logica (OR-gate), caratterizzato dalla presenza del segnale in uscita quando è presente un segnale in una delle entrate (fig. 1A); l’operatore elementare di prodotto logico (AND-gate), caratterizzato dalla presenza del segnale in uscita quando è presente il segnale in ciascuna delle entrate (fig. 1B); l’operatore logico elementare di inversione o invertitore (NOT-gate o inverter), caratterizzato dalla presenza del segnale in uscita quando non è presente il segnale nell’unica entrata (fig. 1C). Mediante l’uso di tali circuiti è possibile determinare una rete logica, atta a realizzare una prefissata relazione funzionale tra il segnale in uscita e i segnali in entrata; è ovvio che, data l’identità fra alcune relazioni, una stessa dipendenza può essere realizzata mediante più schemi logici; così, l’operatore NOR (fig. 1D) può essere realizzato con gli schemi logici di fig. 2A e fig. 2B, mentre l’operatore NAND (fig. 1E) può essere ottenuto con i circuiti l. di fig. 2C e fig. 2D. La funzione logica di non equivalenza (fig. 1F) può essere realizzata mediante il diagramma logico riportato in fig. 3A o con quello in fig. 3B, che deriva dall’impiego esclusivo dell’operatore NOR.
Per quanto sia possibile la realizzazione di circuiti l. mediante qualunque tipo di dispositivi atti ad assumere due sole configurazioni diverse, attualmente, stante l’elevatissima velocità di commutazione normalmente richiesta, tali dispositivi sono realizzati mediante componenti elettronici. I circuiti l. trovano la loro principale applicazione negli elaboratori elettronici numerici, che si servono appunto della numerazione binaria.
Circuiti l. elettronici
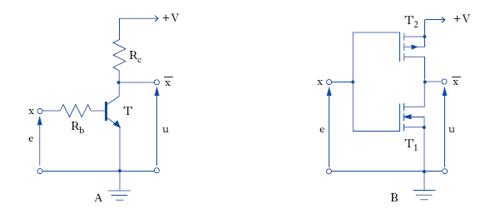
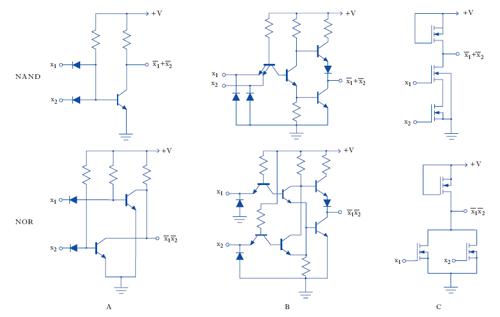
È possibile sfruttare l’unidirezionalità della conduzione elettrica nei diodi per realizzare operatori a diodi di somma logica e di prodotto logico. Tuttavia, mediante l’impiego esclusivo di diodi non è possibile la realizzazione di un qualunque circuito di commutazione in quanto non può essere eseguita l’operazione di inversione; per tale operazione risulta necessario l’impiego di elementi attivi (per es., transistori di tipo bipolare, BJT, o a effetto di campo, CMOS), che assolvono contemporaneamente anche il compito di aumentare il livello dei segnali impiegati nella rete, compensando le inevitabili attenuazioni introdotte dagli elementi passivi. In fig. 4 sono riportati 2 circuiti che realizzano un invertitore utilizzando rispettivamente un transistore bipolare T (fig. 4A), o due transistori a effetto di campo complementari T1 e T2 (fig. 4B). Se nel circuito di fig. 4A la tensione d’ingresso, e, è nulla (valore logico 0), il transistore è spento e si ha una tensione di uscita u pari a +V (valore logico 1). Se la tensione di ingresso, e, è pari a +V, con una opportuna scelta del valore del resistore Rb si ha una forte conduzione di corrente nel transistore e, a causa della conseguente forte caduta di tensione ai capi del resistore Rc, la tensione di uscita è praticamente nulla. Nel circuito di fig. 4B, poiché i 2 transistori sono complementari (cioè, T1 è a canale n mentre T2 è a canale p), la conduzione di uno dei due corrisponde all’interdizione dell’altro. Così, quando e è nulla T1 è interdetto mentre T2 è in conduzione, per cui la tensione di uscita u è pari a +V. Se invece la tensione di ingresso, e, è pari a +V, T2 è interdetto, T1 conduce e la tensione u è nulla. Nella fig. 5 sono schematizzati circuiti a transistori che realizzano le operazioni NAND e NOR, mediante le quali, come accennato prima, è possibile realizzare ogni altra operazione logica; in questi schemi, detti a logica positiva, il valore logico 1 corrisponde alla presenza di tensione positiva o anche alla non connessione, il valore logico 0 al cortocircuito verso massa. Grandi vantaggi, specialmente dal punto di vista della riduzione dell’ingombro e dell’uniformità dei singoli circuiti, derivano dalla sostituzione di circuiti a componenti discreti con circuiti integrati nella realizzazione dei circuiti logici. Si sono così realizzati circuiti l. integrati, di piccolissime dimensioni, detti circuiti micrologici, che attuano più circuiti logici o un’intera rete logica. Dato che nella tecnica dei circuiti integrati il costo di realizzazione è poco influenzato dal minore o maggior numero dei componenti (diodi, transistori, resistori), nei circuiti micrologici non è antieconomico, come sarebbe nei circuiti ordinari, realizzare gli operatori logici con un maggior numero di componenti, al fine di ottenere migliori prestazioni. A titolo di esempio, nella fig. 5B è riportato lo schema di operatori NAND e NOR integrati. I circuiti l. integrati realizzati con una stessa tecnologia e con caratteristiche tali da poterli combinare direttamente tra di loro costituiscono una famiglia di circuiti logici. Sono in uso varie sigle, tratte dall’inglese, per contraddistinguere le varie famiglie di circuiti l.: per es., la sigla DTL (diode transistor logic) indica circuiti, come quelli della fig. 5A, che usano diodi all’entrata, mentre la sigla TTL (tran;sistor transistor logic) indica circuiti, come quelli della fig. 5B, in cui anche l’entrata dei segnali è affidata a transistori, eventualmente a più emettitori (un emettitore per ogni entrata, negli operatori NAND e simili). La famiglia ECL (emitter coupled logic) evita la saturazione dei transistori e quindi consente velocità di funzionamento molto elevate. La famiglia MOS (metal-oxide se;miconductor) ad aumento di canale n (o N-MOS) consente i più elevati valori di densità di componenti sull’integrato, e circuiti come quelli illustrati nella fig. 5C trovano larga applicazione nelle memorie dei microprocessori. La famiglia CMOS (complementary MOS) permette di realizzare circuiti l. (fig. 4B) per i quali è necessaria una ridottissima potenza di alimentazione, e per tale motivo trovano ampia diffusione.