superfluidità

superfluidità In fisica, proprietà di un liquido di fluire senza attrito, cioè con viscosità praticamente nulla.

Caratteri generali

fig. 1

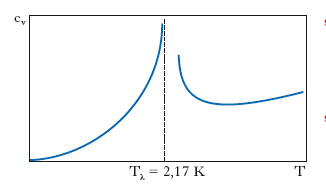
La s. si manifesta per temperature e per velocità di trasporto inferiori a determinati valori critici specifici. L’elio con numero di massa 4 (42He) nello stato liquido è stato il primo sistema a mostrare la s. (elio II, fig. 1) al di sotto della temperatura criticaTλ=2,17 K, come fu osservato dapprima a partire da alcune peculiarità nelle proprietà termodinamiche e poi, negli anni 1936-38, a partire da aspetti più strettamente dinamici e di trasporto. La s. si può, almeno parzialmente, ricondurre a una condensazione analoga a quella di Bose-Einstein (➔ statistica) e tutti i liquidi composti, come l’4He, da atomi a spin intero, cioè che obbediscono alla statistica di Bose-Einstein, dovrebbero a temperature prossime allo zero assoluto divenire superfluidi; ma solo l’4He rimane liquido a queste temperature.

La s. dell’elio con numero di massa 3 (32He) fu scoperta solo all’inizio degli anni 1970, in quanto si manifesta a temperature molto più basse, Tc=2,7 mK, immediatamente vicino alla curva di coe;sistenza con il solido. Poiché gli atomi dell’3He hanno spin semintero, e quindi obbediscono alla statistica di Fermi-Dirac, il meccanismo della s. è in questo caso più complesso: sotto l’azione di debolissime forze attrattive interatomiche di van der Waals si formano coppie di atomi legati molto debolmente (di qui il valore estremamente basso della temperatura critica), che, avendo spin intero, obbediscono alla statistica di Bose-Einstein.

Per alcune particolarità della propagazione di onde elastiche nei superfluidi ➔ suono.

Fenomenologia dell’4He

fig. 2

fig. 3

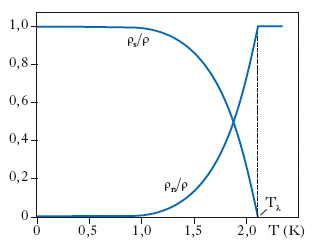
Il calore specifico tende ad aumentare in funzione della temperatura quando ci si avvicina al valore critico per la transizione superfluida a partire sia da temperature più basse, sia da temperature più alte, acquistando la forma peculiare della lettera greca λ, da cui la denominazione Tλ per la temperatura critica di questa transizione (fig. 2). L’andamento è quello proprio delle transizioni di fase disordine-ordine di seconda specie: passando, quindi, per la temperatura Tλ il sistema si ordina. Questo è confermato dal fatto che, in base all’andamento della curva di coesistenza tra il liquido superfluido e il solido (che tende a essere orizzontale a basse temperature; fig. 1), si può dedurre che l’elio nelle due fasi ha circa la stessa entropia, cioè il liquido superfluido è ordinato quanto il solido. Tuttavia, quest’ordine non può essere di natura spaziale come per il solido, perché esperimenti di diffrazione di raggi X non mostrano differenze tra la struttura dell’elio liquido normale sopra Tλ e di quello superfluido sotto Tλ. Anzi, immediatamente sotto Tλ la densità dell’elio decresce invece di crescere al diminuire della temperatura, indicando una preferenza per una distribuzione spaziale allargata. I valori della viscosità dinamica η dell’elio al di sotto di Tλ, misurati dalla capacità dell’elio di passare attraverso capillari sottili (η<10–12 Pa∙s), sono almeno un milione di volte più piccoli di quelli misurati dallo smorzamento delle oscillazioni di un pendolo di torsione immerso nel liquido (η≃10−6 Pa∙s). Quest’enorme differenza, insieme ad altre numerose indicazioni sperimentali, ha portato al modello dei due fluidi: si assume che il liquido sia costituito da due componenti non separabili compenetrantisi, di cui una, detta normale, è viscosa e portatrice di entropia, l’altra, superfluida, è non viscosa, con entropia nulla e quindi altamente ordinata. Nel capillare passa solo la componente superfluida e si misura, quindi, una viscosità bassissima; con il pendolo di torsione, invece, si risente dell’effetto della componente normale e si misura quindi il valore più elevato della viscosità. Allo zero assoluto, c’è solo la componente superfluida, mentre, all’aumentare della temperatura, si forma la componente normale che si comporta in modo simile a un gas. La densità ρn della componente normale aumenta lentamente e quindi rapidamente, finché a Tλ coincide con la densità totale ρ. Viceversa, la densità del superfluido ρs va a zero al punto critico e coincide con la densità totale ρ allo zero assoluto (fig. 3). Se si considera l’elio, in prima approssimazione, come un gas di bosoni non interagenti, si ha la condensazione di Bose-Einstein, consistente nel fatto che a temperature inferiori a un certo valore critico Tc (che dipende dalla densità) ha luogo l’occupazione macroscopica di un singolo stato. Sembrerebbe a questo punto naturale identificare la componente superfluida dell’elio con la frazione (pari a 1 allo zero assoluto e a 0 alla temperatura critica) di atomi di elio che ha subito la condensazione di Bose-Einstein. Per di più, se si inserisce il valore sperimentale della densità dell’elio nella formula per la temperatura critica di un gas di Bose, si ottiene Tc≃3,4 K, valore non troppo diverso, data la semplicità del modello, dal valore sperimentale di Tλ. La condensazione di Bose-Einstein darebbe anche luogo all’ordinamento del sistema in uno spazio diverso dallo spazio ordinario, cioè nello spazio delle quantità di moto, come richiesto dai dati sperimentali. Tuttavia, un gas di Bose non può essere un modello realistico di superfluido in quanto non prevede l’esistenza di una velocità di trasporto critica al di sopra della quale non può aversi superfluidità. Si deve, quindi, tener conto dell’interazione tra gli atomi oltre che della loro statistica. Gli atomi di elio in interazione devono avere uno stato fondamentale che dia luogo a eccitazioni di quasiparticelle compatibili con l’esistenza della velocità critica e, allo stesso tempo, presenti il fenomeno di condensazione di Bose-Einstein (generalizzandone le proprietà ai sistemi interagenti).

Abstract di approfondimento da Superconduttività e superfluidità di Carlo Di Castro, Sergio Caprara, Marco Grilli (Enciclopedia della Scienza e della Tecnica)

La superfluidità è il fenomeno per cui alcuni sistemi presentano viscosità nulla e possono quindi fluire senza dissipare energia. La superfluidità si manifesta per velocità di flusso e temperature inferiori a determinati valori critici, specifici di ciascun sistema. Partendo dall’osservazione sperimentale di anomalie nelle proprietà termodinamiche e di trasporto, si scoprì che l’elio liquido con numero isotopico 4 (⁴He) diventa superfluido (elio II) alla temperatura critica T_l=2,17 K. La superfluidità dell’elio con numero isotopico 3 (³He) si manifesta a temperature molto più basse e fu scoperta solo nel 1971, perché il raggiungimento di temperature così basse richiedeva l’impiego di tecnologie più avanzate. La transizione, vicino alla curva di coesistenza con la fase solida, avviene alla temperatura critica T_c=2,7 mK.

All’assenza di viscosità nei superfluidi corrisponde l’assenza di resistenza elettrica per il moto degli elettroni di molti metalli, al di sotto di temperature critiche con valori tipici T_c≈1÷10 K, che risultano inversamente proporzionali alla radice della massa isotopica degli ioni che costituiscono il reticolo cristallino (effetto isotopico). Il fenomeno, detto superconduttività, fu scoperto da Heike Kamerlingh Onnes nel mercurio, con T_c=4 K. Temperature critiche più elevate sono state ottenute in leghe metalliche e successivamente in alcuni ossidi di rame che, normalmente isolanti, presentano il fenomeno della superconduttività ad alta temperatura (T_c≈30÷150 K) se opportunamente trattati. Lo stato superconduttivo, oltre che dalla resistenza elettrica nulla, è caratterizzato dall’espulsione del campo magnetico: il campo d’induzione magnetica B all’interno d’un superconduttore immerso in un campo magnetico H, d’intensità inferiore a un valore critico H_c, è nullo (effetto Meissner-Ochsenfeld).

L’elio è il più semplice elemento dopo l’idrogeno e presenta un’interessante varietà di comportamenti a bassa temperatura. A causa della piccola massa e della debolezza della parte attrattiva dell’interazione di van der Waals tra gli atomi, con diametro d=2,7 Å, l’He condensa nella fase liquida a temperature molto basse (l’⁴He è liquido al di sotto di 4,2 K) ed è l’unico elemento che resta liquido fino alle più basse temperature raggiunte e solidifica solo sotto alte pressioni. I due isotopi ³He ed ⁴He hanno comportamenti molto diversi che non possono essere ricondotti alla sola differenza di massa isotopica. Infatti, l’³He ha spin semintero e obbedisce, come gli elettroni, alla statistica di Fermi-Dirac: ogni stato quantistico di particella singola può essere occupato al più da una sola particella (principio d’esclusione di Pauli). L’⁴He, invece, ha spin zero e obbedisce alla statistica di Bose-Einstein: ogni stato quantistico può essere occupato da un numero arbitrario di particelle e ciò può dar luogo, in opportune condizioni, alla condensazione di Bose-Einstein. In questo caso, si ha un’occupazione macroscopica d’uno stato di particella singola.

Per comprendere la superfluidità e la superconduttività dobbiamo dapprima spiegare perché i rispettivi stati di flusso siano stabili (o meglio metastabili su tempi estremamente lunghi), anche se, per esempio nell’He, le interazioni tra gli atomi del liquido e le pareti del tubo in cui avviene il flusso sono più intense delle forze intermolecolari e dovrebbero tendere a frenare il moto ordinato. Deve esistere un meccanismo che impedisce il processo viscoso o resistivo, ossia la conversione dell’energia cinetica, associata al moto ordinato del fluido, in energia termica del moto disordinato dei singoli costituenti. Nel 1941 Lev  Davidovič Landau stabilì un criterio di superfluidità sotto l’ipotesi che i sistemi in questione potessero scambiare energia con l’esterno solo attraverso la creazione o la distruzione d’eccitazioni elementari (quasi particelle) con energia ε e quantità di moto p ben definite e legate tra loro da una determinata relazione ε=ε (p) (legge di dispersione), specifica di ciascun sistema. Nei liquidi isotropi l’energia delle eccitazioni dipende solo dal modulo della quantità di moto p≡|p|. Le leggi di conservazione d’energia e quantità di moto associate alla possibilità d’eccitazione delle quasi particelle implicano che il moto del fluido possa essere attenuato solo se la velocità del flusso è maggiore d’una velocità critica v_c = [ε(p)/p]_min cioè pari al minimo della funzione ε(p)/p sulla curva di dispersione di quasi particella. L’esistenza d’un valore minimo non nullo costituisce una condizione necessaria di superfluidità Un sistema gassoso non può essere un modello di superfluido, in quanto per lo spettro d’eccitazione di particella singola ε(p)=p²/2m, si ha v_c=0, dove m è la massa delle particelle.