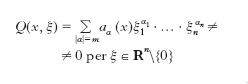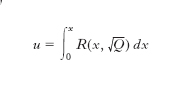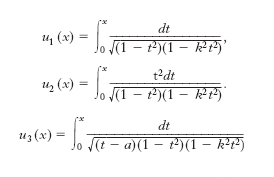ellittico

Botanica

Si dice di un organo (per es., una foglia) quando il suo contorno ha quasi esattamente la forma di un ellisse, ha cioè i due estremi arrotondati; oppure, meno propriamente, quando i due estremi sono piuttosto acuti, con la lunghezza superante la larghezza da più di una fino a tre volte.

Fisica

Detto di fenomeno il cui andamento è descritto da un diagramma a forma di ellisse o da un’equazione analoga a quella di un’ellisse, per es.: polarizzazione e., quella riscontrabile nella luce, nelle radioonde ecc.

Matematica

Operatori e. Particolari tipi di operatori differenziali definiti come segue: sia α=( α₁,…, α_n) una n-upla di interi α_k=0,1,2,… e ξ =(ξ₁,…, ξ_n) un vettore nello spazio euclideo n-dimensionale Rⁿ, e si

definiscano |α| = α₁+…+α_n, D_k= ^∂−−−_∂x^k ; un

operatore L= ∑_∣α∣≤ma_α (x) D₁^α1 ∙ … ∙ D_n^αn, con

a_α(x) funzioni reali, è detto e. (di ordine m) se in ogni punto x del proprio dominio (⊆Rⁿ) si ha

cioè la forma caratteristica Q è definita. In tal caso m è pari e si può normalizzare L imponendo che (−1)^m/2 Q(x,ξ)>0 per ξ≠0. Lo studio degli operatori e. è strettamente collegato a quello delle equazioni e. alle deri;vate parziali, che hanno la forma L f(x)=0 (➔ equazione). Un esempio di operatore e. che compare spesso in fisica è il Laplaciano

∇²= ⁿ∑_i=1 ^∂2−−−∂x_i2 . Menzioniamo infine che la

definizione di operatore e. può essere generalizzata per includere il caso in cui le funzioni a_α(x) siano complesse. Integrali e. La lunghezza di un arco di ellisse (come pure di iperbole, di cicloide, di lemniscata ecc.) è espressa da integrali della forma

,

dove R denota una funzione razionale dei suoi due argomenti e Q un polinomio generico di 3° o 4° grado nella variabile x. Integrali di tale forma si dicono perciò e.: A.-M. Legendre mostrò che essi sono riducibili a tre forme tipiche, rispettivamente integrali e. di prima, di seconda e di terza specie, che si possono scrivere nella forma:

dove a e k sono delle costanti (gli integrali scritti risultano, in generale, integrali di una funzione complessa). Funzioni e. Se si inverte l’integrale e. di prima specie, cioè se si considera l’estremo superiore x come funzione del valore u dell’integrale, si ottiene una funzione a un solo valore in tutto il piano, che ammette a distanza finita solo singolarità polari ed è dotata di una doppia periodicità. Ogni funzione analitica a un sol valore in tutto il piano complesso godente di tali proprietà viene chiamata funzione e. (K.G.J. Jacobi, K. Weierstrass). Una loro generalizzazione sono le funzioni abeliane.

Curve e. Curve algebriche, le coordinate dei cui punti si possono esprimere come funzioni e. di un parametro; esse si presentano come le più semplici dopo le curve razionali (le coordinate dei punti delle quali sono funzioni razionali di un parametro), le curve e. sono di genere 1, quelle razionali di genere 0. Il più semplice esempio di curva e. è la cubica piana priva di punto doppio.