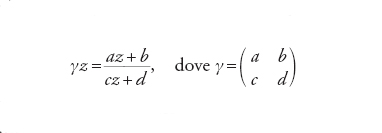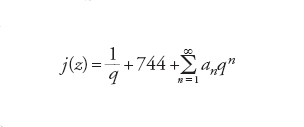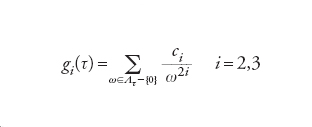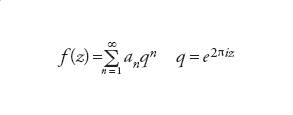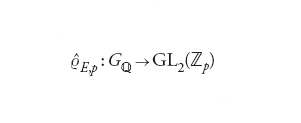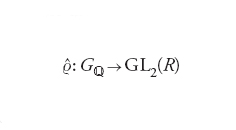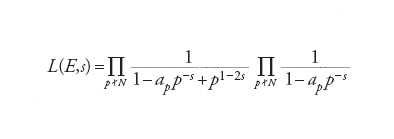Fermat, ultimo teorema di

Fermat, ultimo teorema di

"Cubum autem in duos cubos, aut quadrato quadratum in duos quadrato quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos ejusdem nominis fas est dividere: cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet". La dimostrazione di quest'affermazione di Pierre de Fermat, formulata intorno al 1630 in una famosa nota a margine e conosciuta come ultimo teorema di Fermat, ha eluso gli sforzi di matematici illustri (e meno illustri) sino agli ultimi anni del XX sec., quando il matematico inglese Andrew Wiles, con la collaborazione di Richard Taylor, ha risolto finalmente il dilemma. In linguaggio più moderno, l'ultimo teorema di Fermat (UTF) afferma che l'equazione

xⁿ+yⁿ=zⁿ

non ha soluzioni intere (x,y,z), con x,y,z≠0, per ogni esponente n≥3. Si tratta di un'affermazione di disarmante semplicità, la cui dimostrazione sfrutta tuttavia sofisticate e profonde teorie matematiche sviluppate nel corso dei secoli (in particolare negli ultimi cinquant'anni) e combinate genialmente da Wiles. Queste teorie affondano le loro radici in due importanti filoni di sviluppo della matematica: la costruzione delle estensioni algebriche del campo razionale ℚ e la teoria delle forme modulari. Come quasi sempre accade per le scoperte matematiche importanti, la dimostrazione dell'UTF si inquadra nella continuità dello sviluppo delle idee in matematica, rappresentandone una delle massime sommità.

Nonostante Fermat avesse affermato di possedere una dimostrazione mirabile della sua nota a margine, egli ci lasciò una dimostrazione scritta soltanto del caso n=4. Circa cento anni più tardi, nel 1753, Leonhard Euler fu in grado di dimostrare il caso n=3; nel 1825 Peter Gustav, Lejeune Dirichlet e Adrien-Marie Legendre riuscirono a trattare il caso n=5, mentre nel 1839 il caso n=7 si arrese all'attacco di Gabriel Lamé. Da questi lavori emerge il metodo della discesa infinita, che resta a tutt'oggi fondamentale nello studio delle soluzioni intere di un'equazione algebrica. Grazie al lavoro di Fermat nel caso n=4 e tenuto conto del fatto che ogni esponente n≥4 è sempre divisibile per 4 oppure per un primo dispari p, l'UTF si riduce a dimostrare che l'equazione di esponente primodispari

[2] x^p+y^p=z^p

non ha soluzioni non banali nell'anello degli interi ℤ.

Una svolta fondamentale nei tentativi di dimostrazione del UTF avvenne verso la fine degli anni Trenta del XIX secolo per opera di Kummer. In linguaggio moderno, il suo procedimento dimostrativo si basava sulla fattorizzazione della [2] e sull'aritmetica dell'anello degli interi algebrici di un corpo ciclotomico. Dirichlet gli fece osservare, con un controesempio, che, contrariamente a quanto assumeva Kummer, non tutti gli anelli di interi algebrici sono domini a fattorizzazione unica. Nell'intento di ristabilire la fattorizzazione unica Kummer introdusse certi numeri 'ideali', che svolgono il ruolo di massimi comun divisori degli interi algebrici. Le idee di Kummer portarono alla nascita della teoria degli ideali di un anello, ed ebbero un ruolo fondamentale nei successivi sviluppi della teoria dei numeri, fino a riapparire in forme nuove e inaspettate nella dimostrazione di Wiles. Come Kummer, infatti, anche Wiles è partito dalla supposizione, per assurdo, che la [2] ammetta una soluzione intera. Allo scopo di mostrare che questa supposizione porta a una contraddizione Wiles (con l'aiuto determinante del suo allievo Richard Taylor) si è avvalso dell'enorme bagaglio di conoscenze di teoria dei numeri e geometria algebrica ottenuto dai tempi di Kummer. In sostanza, la dimostrazione dell'UTF è ricondotta alla dimostrazione di una congettura formulata da Shimura e Taniyama sulle curve ellittiche. L'idea di associare a un'ipotetica soluzione dell'equazione di Fermat una curva ellittica, come hanno fatto Wiles e Taylor, si è presentata inizialmente nei lavori di Yves Hellegouarch. La dimostrazione della congettura per la classe delle curve ellittiche semistabili da parte di Wiles e Taylor ha consentito infine di ottenere la dimostrazione dell'UTF, dopo oltre trecento anni di inutili tentativi. D'altra parte, il lavoro di Wiles e Taylor costituisce solo l'inizio della ricerca di soluzione di problemi fondamentali di teoria dei numeri, come la dimostrazione della congettura di Birch e Swinnerton-Dyer, la più importante questione aperta nell'aritmetica delle curve ellittiche.

sommario

1. Il lavoro di Kummer . 2. Estensioni abeliane di ℚ. 3. Estensioni esplicite di campi e funzioni modulari. 4. Curve ellittiche ed estensioni non abeliane di ℚ. 5. Rappresentazioni associate a forme modulari e la congettura di Shimura-Taniyama. 6. La dimostrazione di Wiles. 7. Altri aspetti. □ Bibliografia.

Il lavoro di Kummer

Il contributo di Ernst Eduard Kummer allo studio dell'UTF rappresenta l'inizio di una nuova fase storica, in cui per la prima volta è ottenuto un risultato generale (cioè relativo a tutti gli esponenti) basato su tecniche profonde della teoria algebrica dei numeri. Alla base del metodo vi è l'osservazione che l'equazione di Fermat per l'esponente p si fattorizza come

[3] (x+y)(x+ζ_py)…(x+ζ_p^p−1y)=z^p

dove z^p indica la radice p-esima primitiva dell'unità e^2πi/p. Supponendo che una soluzione intera esista, questa formula può essere interpretata come una relazione tra gli elementi dell'anello ℤ[ζ_p], composto da tutti i numeri complessi della forma a₀+a₁ζ_p+…+a_p−1ζ_p^p−1 con gli a_i interi. È naturale chiedersi sotto quali condizioni essa comporti che ciascun fattore x+ζ_p^ky sia essenzialmente uguale alla potenza p-esima di un elemento di ℤ[ζ_p].

Assumendo l'esistenza di una soluzione (x,y,z) con x,y,z≠0, Kummer cercò di ottenere una contraddizione. Si noti che non è una limitazione supporre che x, y e z non abbiano fattori comuni maggiori di 1. Si consideri dapprima il caso in cui p non divide xyz (questo è il cosiddetto primo caso dell'UTF). Se nell'anello ℤ[ζ_p] vale la proprietà di fattorizzazione unica (come prodotto di fattori primi) ben nota per l'anello ℤ, si dimostra che x+ζ_p^ky è della forma uα^p, dove u è un'unità e α un elemento in ℤ[ζ_p]. Da questa relazione si può ricavare una contraddizione. Tale dimostrazione introduce un importante interrogativo sulla struttura algebrica dell'anello ℤ[ζ_p], che ha stimolato la nascita della teoria dei numeri moderna. La fondamentale scoperta (descritta nel linguaggio dei giorni nostri) fu che la proprietà di fattorizzazione unica in ℤ[ζ_p] vale soltanto per un numero finito di esponenti p (quelli minori di 23) e che tuttavia una proprietà analoga è sempre valida per gli ideali non nulli di quest'anello (un ideale I di ℤ[ζ_p] è un sottoanello tale che se i appartiene a I anche a∙i appartiene a I per ogni a in ℤ[ζ_p]). In base a questa proprietà ogni ideale non nullo di ℤ[ζ_p] può essere fattorizzato in modo essenzialmente unico come prodotto di ideali primi. Da questo segue che l'ideale principale (x+ζ_p^ky) è uguale alla potenza p-esima di un ideale I:

[4] (x+ζ_p^ky)=I^p.

Si definisce una relazione di equivalenza I∼J sull'insieme degli ideali non nulli di ℤ[ζ_p] dichiarando equivalenti I e J se esistono elementi non nulli α e β di ℤ[ζ_p] tali che αI=βJ. La moltiplicazione di ideali induce una struttura di gruppo abeliano sull'insieme quoziente Cl_p, detto gruppo delle classi di ideali. Kummer dimostrò la finitezza di Cl_p e ottenne dei criteri per determinare se p divida o meno l'ordine h_p (ovvero il numero di elementi) di Cl_p. Il primo p è chiamato regolare se non divide h_p e irregolare se invece divide h_p. Se p è un primo regolare, l'uguaglianza (x+ζ_p^ky)I^p implica che I è un ideale principale (α) e quindi vale la relazione x+ζ_p^ky=uα^p, che si sarebbe ottenuta direttamente assumendo la proprietà di fattorizzazione unica per gli elementi di ℤ[ζ_p]. Da questa relazione si può ricavare una contraddizione, dimostrando così il primo caso dell'UTF per esponenti primi regolari. Il secondo caso (in cui p divide uno tra x, y e z) può essere trattato con considerazioni analoghe. Fu seguendo queste linee di ragionamento che Kummer ottenne la dimostrazione dell'UTF per tutti gli esponenti primi regolari. La sorte vuole che a tutt'oggi non si sappia dimostrare l'esistenza di infiniti primi regolari, nonostante questi sembrino presentarsi con maggiore frequenza di quelli irregolari, dei quali è dimostrata l'infinità. A dispetto di queste limitazioni del metodo di Kummer, le idee da lui introdotte nello studio degli anelli ℤ[ζ_p] (e di certe loro generalizzazioni, chiamate anelli degli interi algebrici di campi di numeri) avranno un ruolo fondamentale nello sviluppo della teoria dei numeri e riappariranno in forme nuove e inaspettate nella dimostrazione di Wiles.

Estensioni abeliane di ℚ

Le idee di Kummer sono profondamente legate alla teoria delle estensioni abeliane del campo razionale ℚ. Sia α un numero algebrico, cioè un numero complesso che soddisfi un'equazione algebrica p(x)=0, dove p(x) è un polinomio irriducibile a coefficienti razionali non tutti nulli. Indichiamo con ℚ(α) il campo generato da α: gli elementi di ℚ(α) sono le espressioni polinomiali in α a coefficienti razionali. Il campo ℚ(α) è chiamato estensione algebrica finita di ℚ; questa estensione si dice di Galois se ℚ(α) contiene tutte le radici complesse di p(x)=0. In questo caso, si definisce il gruppo di Galois Gal(ℚ(α)/ℚ) dell'estensione ℚ(α) come il gruppo degli automorfismi di ℚ(α), rispetto alla composizione di applicazioni (un automorfismo di ℚ(α) è un'applicazione di ℚ(α) in sé che rispetta le operazioni di somma e prodotto). Per descrivere un automorfismo σ basta specificare l'immagine σ(α) di α, che è necessariamente un'altra radice di p(x)=0 (coincidente con α se σ è l'applicazione identica). Un'estensione di Galois ℚ(α) si dice abeliana se il suo gruppo di Galois è un gruppo abeliano (ossia commutativo).

Come esempio, si consideri l'm-esimo campo ciclotomico, definito come l'estensione ℚ(ζ_m), dove ζ_m indica la radice primitiva m-esima dell'unità e^2πi/m, soddisfacente l'equazione x^m−1=0. Si verifica che ℚ(ζ_m) è un'estensione abeliana di ℚ; in effetti, vi è un isomorfismo

[5] Gal(ℚ(ζ_m)/ℚ)≃(ℤ/mℤ)^×

dove (ℤ/mℤ)^× è il gruppo delle unità nell'anello ℤ/mℤ delle classi di resti modulo m. Questo isomorfismo è definito inviando un elemento σ del gruppo di Galois di ℚ(ζ_m) nell'unità k modulo m tale che σ(ζ_m)=ζ^k_m. Si noti che (ℤ/mℤ)^× può essere identificato con il gruppo GL₁(ℤ/mℤ) delle matrici invertibili di ordine uno a coefficienti in ℤ/mℤ. Nel seguito, si utilizzerà la notazione GL₁(ℤ/mℤ) per indicare (ℤ/mℤ)^×, al fine di mettere in evidenza l'analogia con costruzioni che saranno introdotte nei prossimi paragrafi. Il teorema di Kronecker-Weber, dimostrato nella seconda metà dell'Ottocento, afferma che ogni estensione abeliana finita F di ℚ è contenuta in un campo ciclotomico ℚ(ζ_m) per un certo m. Sia ℚ⁻ la chiusura algebrica di ℚ, cioè l'unione di tutte le estensioni algebriche finite del campo razionale (viste come sottocampi del campo complesso ℂ), e sia ℚ(ζ_∞) l'unione di tutti i campi ciclotomici. Grazie al teorema di Kronecker-Weber, ℚ(ζ_∞) è l'estensione abeliana massimale di ℚ. Se G_ℚ indica Gal(ℚ⁻/ℚ), ne consegue che Gal(ℚ(ζ_∞)/ℚ) si identifica con il quoziente abeliano massimale G_ℚ ^ab di G_ℚ. In particolare, dall'inclusione di ℚ(ζ_m) in (ℚ(ζ_∞) si ottiene per ogni m un omomorfismo suriettivo

[6] ϱ_m: G_ℚ→GL₁(ℤ/mℤ).

Diremo che ϱ_m è una rappresentazione galoisiana di G_ℚ in GL₁ e che ℚ(ζ_m) è un'estensione di ℚ di tipo GL₁. Si osservi che il metodo di Kummer è intimamente legato all'idea di associare a un'ipotetica soluzione dell'equazione di Fermat di esponente p l'estensione ℚ(ζ_p)/ℚ di tipo GL₁, ossia l'estensione definita dall'equazione x^p−1=0 nell'incognita x. Un passo cruciale nella dimostrazione di Wiles consiste nell'associare a un'ipotetica soluzione dell'equazione di Fermat di esponente p un'estensione non abeliana (cioè avente gruppo di Galois non commutativo) di tipo GL₂. Quest'estensione è costruita aggiungendo a ℚ l'insieme finito delle soluzioni di un sistema di equazioni algebriche in due incognite x e y. Un'equazione del sistema è fornita dall'equazione di una curva piana E, detta curva ellittica, associata all'ipotetica soluzione; le altre equazioni descrivono i punti di m-torsione della curva E. Il metodo di Wiles consiste nell'ottenere una contraddizione: esso mostra che l'estensione costruita in questo modo ha proprietà incompatibili tra di loro e perciò non può esistere.

Estensioni esplicite di campi e funzioni modulari

Il teorema di Kronecker-Weber afferma che tutte le estensioni abeliane di ℚ si ottengono aggiungendo i valori della funzione esponenziale e^2πix con esponenti x razionali. È naturale cercare di generalizzare questa affermazione sostituendo al campo razionale ℚ una sua qualsiasi estensione algebrica finita K, detta anche campo di numeri. Il problema è cioè quello di generare le estensioni abeliane di un campo di numeri K per mezzo dei valori di certe funzioni esplicite. Si tratta di una forma del famoso XII problema di Hilbert, formulato all'inizio del XX sec. e ancora del tutto aperto nella sua forma generale. Il caso particolare del problema in cui K sia un campo quadratico immaginario ℚ(√D), con D intero negativo è tuttavia ben compreso: il problema è risolto dalla teoria della moltiplicazione complessa, che rappresenta uno dei culmini della matematica del XIX secolo. Le funzioni esplicite utilizzate in questo caso particolare sono chiamate funzioni modulari.

Vediamone per sommi capi la definizione. Sia X il semipiano superiore complesso, formato dai numeri complessi aventi parte immaginaria strettamente positiva, e sia Γ₀(N) il gruppo moltiplicativo delle matrici quadrate di ordine 2 a coefficienti in ℤ, il cui determinante è uguale a 1 e la cui riduzione modulo N è triangolare superiore. Il gruppo Γ₀(N) agisce su X mediante la regola

[7] formula.

Una funzione modulare di peso k∈ℤ è una funzione meromorfa f definita su X a valori in ℂ, che gode della proprietà (di simmetria rispetto all'azione di Γ₀(N))

[8] f(γz)=(cz+d)^kf(z) per ogni γ∈Γ₀(N)

e che soddisfa una condizione di meromorfia nell'insieme delle cuspidi P₁(ℚ)=ℚ∪{∞}. Una funzione modulare è chiamata forma modulare se è olomorfa ovunque (cuspidi incluse). Una funzione g(z) definita su un disco D di centro z₀ del piano complesso, salvo al più in z₀, si dice olomorfa in D se è differenziabile in senso complesso in tutti i punti di D, e si dice meromorfa in D se è nella forma h(z)/(z−z₀)ⁿ, con n intero, h(z) olomorfa in D e h(z₀)≠0. Se n>0, z₀ è chiamato polo di ordine n. Le funzioni modulari di peso 0 (e quindi invarianti per l'azione di Γ₀(N)) formano un campo rispetto alle operazioni naturali di somma e prodotto. Se N=1, cioè si considerano funzioni invarianti rispetto al gruppo SL₂(ℤ), questo campo è generato da un'unica funzione j(z) caratterizzata dalle proprietà seguenti: ha un polo semplice con residuo 1 nella cuspide ∞, è olomorfa su X e si annulla nel punto e^2πi/3 di X. La forma modulare j ha uno sviluppo in serie di Fourier, detto q-espansione,

[9] formula

dove q=e^2πiz e i coefficienti a_n sono interi; in particolare a₁=196.884 e a₂=21.493.760.

Un caso particolare della teoria della moltiplicazione complessa prende in considerazione le estensioni di K=ℚ(√D) ottenute aggiungendo a K certi valori di j(z). Più precisamente, visto K come sottocampo di ℂ, si consideri una base {1,ω} su ℤ dell'anello O_K degli interi algebrici di K, con ω appartenente a X (per definizione, O_K è il sottoanello di K contenente gli elementi che soddisfano un'equazione algebrica a coefficienti interi, con coefficiente del monomio di grado più alto uguale a 1). Sia poi K il sottocampo di ℂ ottenuto aggiungendo a K tutti i valori j(cω), al variare di c tra gli interi positivi. Il risultato fondamentale della teoria della moltiplicazione complessa afferma che K_∞ è un'estensione (infinita) abeliana di K; inoltre, se K_∞(ζ_∞) indica il minimo campo contenente K_∞ e il campo ciclotomico ℚ(ζ), si ha che K_∞(ζ_∞) è essenzialmente uguale all'estensione abeliana massimale di K.

Curve ellittiche ed estensioni non abeliane di ℚ

Le forme modulari sono legate intimamente alla classificazione delle curve ellittiche sul campo complesso. Una curva ellittica definita su un campo F (di caratteristica diversa da 2 e 3) è una curva proiettiva non singolare rappresentata da un'equazione affine della forma

[10] y²=4x³−g₂x−g₃

con g₂ e g₃ appartenenti a F; la condizione di non singolarità equivale alla condizione g₂³−27g₃²≠0. Sia Λ un reticolo in ℚ, cioè un sottogruppo del gruppo additivo di ℂ della forma ℤω₁+ω₂, con ω₁/ω₂ appartenente a X. Il gruppo quoziente ℂ/Λ è chiamato toro complesso di dimensione uno. I punti complessi di una curva ellittica definita su ℂ si identificano con un toro complesso. Infatti, se Λ_τ indica il reticolo ℤτ+ℤ (con τ∈X), vi è un isomorfismo (definito dalla funzione di Weierstrass e dalla sua derivata) tra ℂ/Λ_τ e i punti complessi E_τ(ℂ) della curva ellittica E_τ di equazione

[11] formula

con c₂=60 e c₃=140. Questo isomorfismo invia l'origine del toro nel punto all'infinito O=(0,1,0) di E_τ. Inoltre, si dimostra che ogni curva ellittica definita su ℂ è isomorfa a E_τ per qualche τ in X. La funzione g_i(τ) è una forma modulare di peso 2i per il gruppo SL₂(ℤ).

Sostituendo a un reticolo Λ=ℤω₁+ω₂ un reticolo omotetico αΛ, α∈ℂ−{0}, si ottiene un toro complesso ℂ/αΛ isomorfo a ℂ/Λ; l'isomorfismo è indotto dalla moltiplicazione per α. Segue che la classe di isomorfismo del toro ℂ/Λ è anche rappresentata dal toro ℂ/Λ_τ, dove τ=ω₁/ω₂. Otteniamo che i punti di X descrivono le classi di isomorfismo dei tori complessi di dimensione uno. Due punti τ e τ′ di X corrispondono alla stessa classe di isomorfismo se e solo se sono coniugati rispetto all'azione di SL₂(ℤ), cioè τ′=γτ per un elemento γ di SL₂(ℤ). Di conseguenza, vi è una biiezione tra X/SL₂(ℤ) e le classi di isomorfismo di tori complessi di dimensione uno.

Il quoziente X/SL₂(ℤ) possiede una struttura naturale di superficie di Riemann, usualmente indicata con Y₀(1). La superficie Y₀(1) è isomorfa alla retta affine complessa e può essere compattificata con l'aggiunta dell'insieme quoziente di cuspidi P₁(ℚ)/SL₂(ℤ), contenente in effetti un solo elemento (rappresentato per esempio da ∞). Questa compattificazione, indicata con X₀(1) e chiamata curva modulare di livello uno, è quindi uguale al quoziente X*/SL₂(ℤ), dove X* indica il semipiano superiore esteso X∪P₁(ℚ). Si tratta di una curva proiettiva, isomorfa a P₁(ℂ).

L'isomorfismo da X₀(1) a P₁(ℂ) è definito esplicitamente per mezzo della forma modulare di peso zero j(τ): infatti, j(τ) è invariante per l'azione di SL₂(ℤ) e quindi può essere vista come una funzione su X₀(1) a valori in P₁(ℂ); questa funzione è biiettiva, poiché j(τ) ha un unico polo semplice nella cuspide di X₀(1). In conclusione, le classi di isomorfismo dei tori complessi di dimensione uno sono parametrizzate dai valori della funzione j(τ). Il gruppo ℂ/Λ_τ è dotato di una struttura naturale di gruppo, in cui l'operazione di somma è indotta dalla somma in ℂ. Questa struttura può essere trasportata su E_τ(ℂ), grazie alla biiezione tra questo insieme e ℂ/Λ_τ, così che diviene possibile sommare i punti complessi della curva ellittica E_τ. Quest'operazione di somma può equivalentemente essere definita in modo geometrico, per mezzo della proprietà seguente: la somma di tre punti P, Q e R (non necessariamente distinti) è uguale al punto all'infinito O (l'origine della legge di gruppo) se e solo se P, Q e R sono allineati.

Fissiamo ora una curva ellittica E definita su ℚ (e quindi anche su ℂ); la struttura di gruppo su E permette di costruire estensioni algebriche di ℚ. Dato un intero m≠2, si indichi con [m] la moltiplicazione per m sui punti complessi di E e sia E[m]={P∈E(ℂ): [m]P=O} il nucleo di [m]. Poiché E(ℂ) è isomorfo a un toro ℂ/Λ, il gruppo E[m] è isomorfo a (ℤ/mℤ)²; fissata una base (P₁,P₂) per E[m] come ℤ/mℤ-modulo, si ottiene un'identificazione del gruppo Aut(E[m]) di automorfismi di E[m] con il gruppo GL₂(ℤ/mℤ) delle matrici invertibili di ordine 2 a coefficienti in ℤ/mℤ. Poiché E è definita su ℚ, la mappa [m] è descritta da funzioni razionali a coefficienti in ℚ; segue che le coordinate affini dei punti non nulli in E[m] definiscono un'estensione di Galois ℚ(E[m]) di ℚ: in altre parole G_ℚ agisce su E[m] per mezzo di automorfismi. Combinando queste osservazioni, grazie alla teoria di Galois si ottiene un omomorfismo

[12] ϱ_E,m:G_ℚ→GL₂(ℤ/mℤ)

detto rappresentazione galoisiana associata ai punti di m-torsione di E. Il nucleo di ϱ_E,m è Gal(ℚ⁻/ℚE[m])) e quindi Gal(ℚ⁻(E[m])/ℚ) si inietta in GL₂(ℤ/mℤ). L'estensione ℚ(E[m])/ℚ sarà detta di tipo GL₂.

È noto che ℚ(E[m])/ℚ può essere ramificata solo nei divisori primi di m e del conduttore N di E. Il conduttore N è un intero positivo che misura la cattiva riduzione di E; in particolare, se un primo p non divide N, la riduzione modulo p di un'equazione per E a coefficienti interi definisce una curva ellittica Ẽ^(p) sul campo finito con p elementi F_p=ℤ/pℤ. Sia O_m l'anello degli interi algebrici in ℚ(E[m]). L'estensione ℚ(E[m])/ℚ è non ramificata in p se l'ideale pO_m di O_m si fattorizza come prodotto di ideali primi distinti di O_m. Se P è uno qualunque di questi fattori primi, l'elemento di Frobenius Frob_P è definito come l'elemento del gruppo di Galois di ℚ(E[m])/ℚ tale che Frob_P(x)x^p appartiene a P per ogni x in O_m. Segue che è possibile definire la matrice ϱ_E,m(Frob_P) corrispondente a Frob_P mediante ϱ_E,m. Se n_p indica la cardinalità dell'insieme finito Ẽ ^(p)(F_p) e se p non divide Nm, si dimostra che valgono le relazioni

[13] tr(ϱ_E(Frob_P))≡1+p−n_p mod m

[14] det(ϱ_E,m(Frob_P))≡p mod m.

La costruzione descritta sopra di un'estensione di tipo GL₂, ottenuta grazie ai punti su una curva ellittica soddisfacenti l'equazione [m]P=0, è analoga alla costruzione dell'estensione ℚ(ζ_m)/ℚ di tipo GL₁ per mezzo delle soluzioni dell'equazione x^m−1=0. Questa seconda costruzione è ottenuta aggiungendo a ℚ i valori della funzione esponenziale negli argomenti razionali; viene da chiedersi se anche la prima costruzione possa essere effettuata in un'opportuna maniera esplicita. Le considerazioni svolte suggeriscono che la teoria delle funzioni modulari può essere di aiuto; vedremo che la questione è legata alla costruzione di rappresentazioni galoisiane associate a forme modulari. La fondamentale congettura di Shimura-Taniyama afferma che la curva ellittica E è associata a una forma modulare f per il gruppo Γ₀(N), nel senso che 1+p−n_p è uguale al p-esimo coefficiente a_p nella q-espansione di f per tutti i primi p che non dividono N. In particolare, per le relazioni messe in evidenza, si ha che se p non divide Nm, a_p(mod m) è uguale alla traccia di ϱ_E,m(Frob_P); diremo in questo caso che ϱ_E,m è associata a f. La dimostrazione della congettura di Shimura-Taniyama da parte di Wiles e Taylor rappresenta l'ultimo atto nella dimostrazione dell'UTF.

Rappresentazioni associate a forme modulari e la congettura di Shimura-Taniyama

L'attenzione sarà ora concentrata sulle forme modulari di peso 2 per il gruppo Γ₀(N), soggette alla condizione di annullamento nelle cuspidi; l'insieme S₂(N) di tali forme possiede la struttura di spazio vettoriale complesso. Data f(z) in S₂(N), il differenziale f(z)dz è invariante per l'azione di Γ₀(N) ed è olomorfo sul semipiano esteso X*. Generalizzando la costruzione della curva modulare di livello uno, definiamo il quoziente

[15] X₀(N) X*/Γ₀(N)

detto curva modulare di livello N. Esso è dotato della struttura di superficie di Riemann compatta e quindi può essere visto come l'insieme dei punti complessi di una curva proiettiva. Ne consegue che S₂(N) si identifica con lo spazio dei differenziali olomorfi su X₀(N); in particolare, per il teorema di Riemann-Roch, ha dimensione finita uguale al genere di X₀(N). Ogni forma f in S₂(N) gode della proprietà di invarianza f(z+1)f(z) e quindi ammette uno sviluppo in serie di Fourier (la q-espansione)

[16] formula.

La variabile q può essere interpretata come un parametro locale nella cuspide ∞. Lo spazio S₂(N) è provvisto di una struttura aggiuntiva: un anello commutativo T_N di endomorfismi definiti esplicitamente in termini delle q-espansioni delle forme modulari, chiamato algebra di Hecke. L'algebra T_N è generata su ℤ da operatori T_n, n≥1, detti operatori di Hecke. Stante l'interpretazione degli elementi di S₂(N) come differenziali olomorfi su X₀(N), T_N può essere identificata con un anello di corrispondenze della curva modulare X₀(N) o, equivalentemente, con un anello di endomorfismi della varietà jacobiana J₀(N) di X₀(N).

Fissata una forma f in S₂(N), si supponga che f abbia coefficienti in ℤ, sia una forma nuova (cioè non provenga da forme per gruppi Γ₀(M) con M divisore proprio di N), sia normalizzata così che a₁=1 e sia un'autofunzione per tutti gli operatori in T_N. Sotto queste ipotesi, valgono le relazioni T_nf=a_nf, dove a_n è l'n-esimo coefficiente nella q-espansione di f. L'assegnazione T_n→a_n definisce un omomorfismo suriettivo di algebre ϕ_f: T_N→ℤ. Indicato con I_f il nucleo di ϕ_f, la varietà quoziente E_f=J₀(N)/I_fJ₀(N) è una curva ellittica definita su ℚ avente conduttore N. La rappresentazione galoisiana

[17] ϱ_f,m:G_ℚ→GL₂(ℤ/mℤ)

associata a f e a un intero m≥2 è per definizione la rappresentazione galoisiana associata ai punti di m-torsione di E_f. Inoltre, se p è un primo che non divide Nm, la traccia di ϱ_f,m(Frob_p) è uguale (modulo m) al p-esimo coefficiente a_p nella p-espansione di f. Questo implica che valgono le relazioni

[18] a_p=1+p−n_p

(dove n_p è la cardinalità di Ẽ_f^(p)(F_p)). Nel caso in cui la forma f in S₂(N) non abbia coefficienti razionali ma goda delle altre precedenti proprietà, una costruzione analoga a quella spiegata sopra permette di associare a f delle rappresentazioni galoisiane. La congettura di Shimura-Taniyama (diventata poi un teorema di Taylor e Wiles) afferma la validità di un converso della costruzione delle rappresentazioni ϱ_f,m. Data una curva ellittica E definita su ℚ, diciamo che ϱ_E,m è irriducibile se per ogni divisore primo p di m non esiste alcun sottospazio di dimensione uno di F_p² invariante per l'azione di G_ℚ su F_p² definita da ϱ_E,p. La congettura di Shimura-Taniyama è la seguente: se E è una curva ellittica definita su ℚ avente conduttore N, esiste una forma f in S₂(N) definita come sopra, tale che ϱ_E,m è isomorfa a ϱ_f,m per ogni m per cui ϱ_E,m è irriducibile. Il significato di questa congettura è che le estensioni di tipo GL₂ ammettono una costruzione esplicita, per mezzo della teoria delle forme modulari. Anche la costruzione esplicita di estensioni abeliane di un campo quadratico immaginario può essere interpretata in termini di rappresentazioni galoisiane associate a una classe di curve ellittiche di tipo speciale, chiamate curve ellittiche con moltiplicazione complessa.

La dimostrazione di Wiles

Conviene schematizzare la strategia dimostrativa in più tappe.

Dalla congettura di Shimura-Taniyama all'ultimoteorema di Fermat: il teorema di Ribet

Come nell'approccio concepito da Kummer, il punto di partenza nella dimostrazione di Wiles consiste nel supporre, per assurdo, che l'equazione di Fermat di esponente p ammetta una soluzione intera (a,b,c) con a,b,c diversi da 0:

[19] a^p+b^p=c^p.

Si può supporre che l'esponente p sia maggiore di 7 (l'UTF è noto dall'Ottocento nei casi p=3,5,7), che a,b,c non abbiano fattori primi comuni e che a≡−1 mod 4 e b≡0 mod 2. Associamo alla soluzione ipotetica (a,b,c) la curva ellittica E=E_a,b,c definita da

[20] y²=x(x−a^p)(x+b^p).

La curva E è semistabile, cioè la singolarità sulla curva ottenuta per riduzione di E modulo ciascun divisore primo del conduttore N è un nodo. La rappresentazione ϱ_E,p associata ai punti di p-torsione di E è irriducibile: questo è affermato dal teorema di Barry Mazur. Inoltre, l'estensione ℚ(E[p])/ℚ definita da ϱ_E,p è non ramificata nei primi diversi da 2 e da p (ciò segue dai fatti generali enunciati nel paragrafo 5 per i primi che non dividono N).

Assumiamo per il momento la validità della congettura di Shimura-Taniyama: esiste cioè una forma modulare f appartenente a S₂(N), tale che ϱ_E,p è associata a f (cioè ϱ_E,pϱ_f,p). Considerate le proprietà di ϱ_E,p, un teorema di Kenneth A. Ribet, detto di abbassamento del livello, afferma l'esistenza di una forma modulare g in S₂(2), con proprietà simili a quelle di f (ma senza necessariamente avere q-espansione a coefficienti razionali), tale che ϱ_E,p è associata a g (cioè ϱ_f,p=ϱ_g,p). In altre parole, la rappresentazione galoisiana associata a E e p può anche essere costruita utilizzando una forma per Γ₀(2). Sappiamo che la dimensione dello spazio S₂(2) è uguale al genere della curva modulare X₀(2). Analogamente al caso di X₀(1), l'insieme dei punti complessi di X₀(2) è isomorfo a P₁(ℂ); in altre parole, la curva X₀(2) ha genere zero. Segue che S₂(2) è lo spazio nullo e quindi la forma g non può esistere: si ottiene così una contraddizione. In conclusione, la dimostrazione dell'UTF è ridotta dai ragionamenti delineati sopra alla dimostrazione della congettura di Shimura-Taniyama; il risultato di Wiles e Taylor consiste nella dimostrazione di questa congettura. L'idea di associare a un'ipotetica soluzione dell'equazione di Fermat una curva ellittica apparve nei lavori di Yves Hellegouarch; più tardi Gerhard Frey comprese che l'esistenza di tale curva poteva essere incompatibile con la congettura di Shimura-Taniyama. Ribet infine, con il suo fondamentale teorema di abbassamento del livello, ha reso queste idee rigorose.

Il teorema di Mazur

Un teorema di Barry Mazur afferma che se un primo p è maggiore di 7, la rappresentazione ϱ_E,p associata ai punti di p-torsione di una curva ellittica E semistabile definita su ℚ è irriducibile, anzi, più precisamente, è suriettiva. Questo teorema si applica in particolare alla curva E=E_a,b,c, come abbiamo visto nel paragrafo precedente, poiché E è semistabile. In altre parole, il gruppo di Galois dell'estensione ℚ(E[p])/ℚ è il più grande possibile, essendo isomorfo a GL₂(F_p). D'altro canto, la contraddizione ottenuta nel paragrafo precedente si basa sul fatto che l'estensione ℚ(E[p])/ℚ è poco ramificata, essendo la ramificazione concentrata nei soli primi 2 e p. La dimostrazione di Mazur si fonda sullo studio della curva modulare X₀(p). Una generalizzazione di quanto spiegato nel caso di X₀(1) mostra che i punti di X₀(p) diversi dalle cuspidi classificano le classi di isomorfismo di coppie (E,C), dove E è una curva ellittica e C un sottogruppo di ordine p di E. Il teorema di Mazur può dunque essere visto come una proposizione diofantea relativa ai punti razionali di X₀(p), analoga all'UTF: esso afferma in particolare che se p è sufficientemente grande, gli unici punti di X₀(p) definiti su ℚ sono le cuspidi.

Il teorema di Langlands-Tunnell

Sia E una curva ellittica su ℚ e si supponga che la rappresentazione ϱ_E,3 associata ai punti di 3-torsione di E sia irriducibile. Sofisticate tecniche analitiche permettono di dimostrare che ϱ_E,3 è sempre associata a una forma modulare f di peso 2, cioè ϱ_E,3=ϱ_f,3. La validità di questo risultato dipende dal fatto che il gruppo GL₂(F₃) è risolubile e può essere immerso in GL₂(ℂ). Si badi che esso non permette di concludere direttamente la validità della congettura di Shimura-Taniyama per E.

La dimostrazione della congettura di Shimura-Taniyama

Cominciamo con una riformulazione della congettura di Shimura-Taniyama. Se E è una curva ellittica definita su ℚ, il modulo di Tate p-adico T_p(E) di E è definito come il limite inverso dei gruppi E[pⁿ], n≥1, rispetto alle proiezioni naturali. Segue che T_p(E) è isomorfo a ℤ_p², dove ℤ_p indica il gruppo additivo degli interi p-adici. Fissata una base per lo ℤ_p-modulo T_p(E), l'azione di G_ℚ su T_p(E) definisce una rappresentazione

[21] formula.

Analogamente, data una forma f in S₂(N) a coefficienti razionali soddisfacente le ipotesi elencate nel paragrafo 5, si associa a f una rappresentazione ‸ϱ_f,p mediante la relazione ‸ϱ_f,p=ϱ_Ef,p, dove E_f è la curva ellittica ivi introdotta. La congettura di Shimura-Taniyama è equivalente all'affermazione seguente: se E è una curva ellittica definita su ℚ di conduttore N, esistono un primo p per cui ϱ_E,p è irriducibile e una forma modulare f∈S₂(N) come sopra, tali che ‸ϱ_E,p è isomorfa a ‸ϱ_f,p. Se ν indica la mappa tra gruppi GL₂ indotta dalla proiezione naturale ℤ_p→ℤ/pℤ, si ha l'uguaglianza

[22] formula.

Diciamo che ‸ϱ_E,p è una deformazione di ϱ_E,p. Supponiamo che ϱ_E,p sia irriducibile. L'approccio di Wiles alla dimostrazione della congettura di Shimura-Taniyama consiste nello studio di tutte le deformazioni di ϱ_E,p della forma

[23] formula

dove R è una ℤ_p-algebra locale, noetheriana e completa, di campo residuo F_p, soddisfacente opportune ipotesi di ramificazione. Grazie a una teoria sviluppata da Mazur, tali deformazioni sono classificate da una deformazione universale corrispondente a un'algebra R_univ. Se la rappresentazione ϱ_E,p è associata a una forma modulare f, è possibile classificare le sue deformazioni associate a forme modulari per mezzo di un anello T, identificato con una certa algebra di Hecke. L'universalità di R_univ implica l'esistenza di un'applicazione

[24] π:R_univ→T.

Mediante l'uso di ingegnosi criteri di algebra commutativa, Wiles e Taylor dimostrano che π è un isomorfismo. Questo significa che tutte le deformazioni di ϱ_E,p sono associate a forme modulari; in particolare lo deve essere ‸ϱ_E′,p e quindi E soddisfa la congettura di Shimura-Taniyama. Il lettore avrà notato che, per poter essere messa in atto, questa strategia richiede di sapere che ϱ_E,p sia irriducibile e sia associata a una forma modulare, per una scelta del primo p. Scegliendo p=3, Wiles invoca a questo punto il teorema di Langlands-Tunnell: se ϱ_E,3 è irriducibile, ciò mette fine al tour de force. Se invece ϱ_E,3 è riducibile, Wiles dapprima osserva che ϱ_E,5 è irriducibile; poi mostra l'esistenza di una nuova curva ellittica E′ tale che ϱ_E′,5 è isomorfa a ϱ_E,5 e ϱ_E,3 è irriducibile; applicando la strategia precedente, ottiene che E′ soddisfa la congettura di Shimura-Taniyama e in particolare che ϱ_E,5 (e per ciò anche ϱ_E,5) è associata a una forma modulare; infine, applicando di nuovo la strategia precedente, questa volta per p=5, dimostra che anche E soddisfa la congettura di Shimura-Taniyama. Due osservazioni per concludere. Il lavoro originale di Wiles e Taylor dimostra la congettura di Shimura-Taniyama per la classe delle curve ellittiche semistabili. Generalizzando le tecniche qui esposte, Christophe Breuil, Brian Conrad, Fred Diamond e Richard Taylor hanno recentemente dimostrato la congettura per tutte le curve ellittiche definite su ℚ. Infine, il criterio di isomorfismo per l'applicazione π che è alla base del metodo dimostrativo corrisponde alla verifica di una formula analitica per il numero di classi di ideali relativa alla rappresentazione aggiunta della curva ellittica: questa formula può essere interpretata come una generalizzazione del criterio di Kummer per la regolarità di un primo p.

Altri aspetti

Sebbene il lavoro di Wiles e Taylor metta la parola fine all'annoso problema posto dalla congettura di Fermat, si può dire che esso rappresenti solo l'inizio del lavoro sulla risoluzione di fondamentali questioni in teoria dei numeri. Una di queste è la congettura di Birch e Swinnerton-Dyer, la più importante questione aperta nello studio dell'aritmetica delle curve ellittiche. Data una curva ellittica E definita su ℚ, sia a_p il coefficiente 1+p−n_p, dove n_p è la cardinalità di Ẽ^(p)(F_p). I coefficienti a_p sono definiti per tutti i primi p di buona riduzione, cioè che non dividono il conduttore N; una definizione analoga permette di determinare a_p anche per i divisori primi di N (in questo caso a_p è sempre uguale a 0, 1 o −1). La funzione L archimedea di E è definita come il prodotto infinito

[25] formula

dove s è una variabile complessa. Una stima degli a_p mostra che L(E,s) converge a una funzione olomorfa se la parte reale di s è maggiore di 3/2. La serie L di E codifica informazioni locali relative alla riduzione di E modulo i primi razionali; la congettura di Birch e Swinnerton-Dyer afferma che L(E,s) esprime proprietà globali di E, concernenti il gruppo E(ℚ) dei punti di E definiti su ℚ. Più precisamente, essa afferma che L(E,s) ammette un prolungamento analitico a tutto il piano complesso; inoltre, l'ordine di annullamento in s=1 di L(E,s) è uguale al rango di E(ℚ) (grazie a un teorema di Louis J. Mordell, il gruppo E(ℚ) è finitamente generato). Come l'UTF determina le soluzioni intere dell'equazione di Fermat, così la congettura di Birch e Swinnerton-Dyer determina il numero delle soluzioni razionali indipendenti dell'equazione cubica E. La dimostrazione della congettura di Shimura-Taniyama implica la prima parte della congettura di Birch e Swinnerton-Dyer e dunque ammette, oltre all'UTF, una nuova applicazione diofantea. Indicata con f la forma modulare associata a E, si definisca la serie L di f mediante un prodotto infinito L(f,s) analogo a L(E,s), in cui il coefficiente a_p è sostituito dal p-esimo coefficiente nella q-espansione di f.

La congettura di Shimura-Taniyama si può riformulare come l'uguaglianza L(E,s)L(f,s). Le proprietà analitiche di f implicano la continuazione analitica di L(f,s) e quindi di L(E,s). La seconda parte della congettura di Birch e Swinnerton-Dyer è nota, grazie ai teoremi di Benedict Gross e Don Zagier e di Victor Kolyvagin, solamente se l'ordine di annullamento di L(E,s) in s=1 è minore o uguale a uno. Negli altri casi, il problema è del tutto aperto. La dimostrazione di questi teoremi è basata in modo essenziale sulla teoria della moltiplicazione complessa. È interessante osservare che la situazione è migliore nel caso delle congetture p-adiche di Birch e Swinnerton-Dyer, nelle quali la funzione L archimedea L(E,s) è sostituita da certi analoghi non archimedei, detti funzioni L p-adiche. Risultati ottenuti negli ultimi anni da diversi autori dimostrano che l'ordine di annullamento di tali funzioni è sempre almeno uguale al rango di E(ℚ). Il problema di comprendere i legami profondi tra le teorie archimedee e quelle p-adiche è una delle più importanti sfide poste dalla teoria dei numeri nel XXI secolo.

bibliografia

Ahlfors 1979: Ahlfors, Lars, Complex analysis, New York,McGraw-Hill, 1979.

Birch, Swinnerton-Dyer 1963: Birch, Bryan - Swinnerton-Dyer, H. Peter F., Notes on elliptic curves (I), "Journal für die reine und angewandte Mathematik", 212, 1963, pp. 7-25.

Birch, Swinnerton-Dyer 1965: Birch, Bryan - Swinnerton-Dyer, H. Peter F., Notes on elliptic curves (II), "Journal für die reine und angewandte Mathematik", 218, 1965, pp. 79-108.

Breuil 2001: Breuil, Christophe e altri, On the modularity of elliptic curves over Q: wild 3-adic exercises, "Journal of the American Mathematical Society", 14, 2001, pp. 843-939.

Darmon 1995: Darmon, Henry - Diamond, Fred - Taylor, Richard, Fermat's last theorem, in: Current developments in mathematics. Proceedings of the Harvard/MIT joint conference held at the American Academy of Arts and Sciences, Cambridge (Mass.), International Press, 1995, pp. 1-154.

Edwards 1977: Edwards, Harold M., Fermat's last theorem: a genetic introduction to algebraic number theory, New York, Springer, 1977.

Gross, Zagier 1986: Gross, Benedict H. - Zagier, Don, Heegner points and derivates of L-series, "Inventiones mathemati-cae", 84, 1986, pp. 225-320.

Kolyvagin 1990: Kolyvagin, Victor A., Euler systems, in: The Grothendieck Festschrift. A collection of articles written inhonour of the 60^th birthday of Alexander Grothendieck, edited by Pierre Cartier e altri, Boston, Birkhäuser, 1990, 3 v.; v. II, pp. 435-483.

Langlands 1980: Langlands, Robert P., Base change for GL(2), Princeton (N.J.), Princeton University Press, 1980.

Marcus 1977: Marcus, Daniel A., Number fields, New York, Springer, 1977.

Mazur 1977: Mazur, Barry, Modular curves and the Eisenstein ideal, "Publications mathématiques de l'Institut des Hautes Études Scientifiques", 47, 1977, pp. 33-186.

Mazur 1978: Mazur, Barry, Rational isogenies of prime degree, "Inventiones mathematicae", 44, 1978, pp. 129-162.

Mazur 1989: Mazur, Barry, Deforming Galois representations, in: Galois groups over Q, edited by Yasutaka Ihara e altri, New York, Springer, 1989, pp. 385-437.

Ribet 1990: Ribet, Kenneth A., On modular representations of Gal(Q/Q) arising from modular forms, "Inventiones mathe-maticae", 100, 1990, pp. 431-476.

Serre 1967: Serre, Jean-Pierre, Complex multiplication, in: Algebraic number theory, edited by John W.S. Cassels, Albrecht Fröhlich, London, Academic Press, 1967, pp. 292-296.

Serre 1973: Serre, Jean-Pierre, A course in arithmetic, New York, Springer, 1973.

Serre 1987: Serre, Jean-Pierre, Sur les représentations modulaires de degré 2 de Gal(Q/Q), "Duke mathematical journal", 54. 1987, pp. 179-230.

Shimura 1971: Shimura, Goro, Introduction to the arithmetic theory of automorphic functions, Princeton (N.J.), Princeton University Press, 1971.

Silverman 1986: Silverman, Joseph, The arithmetic of elliptic curves, New York-London, Springer, 1986.

Taylor, Wiles 1995: Taylor, Richard - Wiles, Andrew, Ring theoretic properties of certain Hecke algebras, "Annals of mathematics", 141, 1995, pp. 553-572.

Tunnell 1981: Tunnell, Jerrold, Artin's conjecture for repres-entations of octahedral type, "Bulletin of the American Mathematical Society", 5, 1981, pp. 173-175.

Washington 1982: Washington, Lawrence, Introduction to cyc-lotomic fields, New York, Springer, 1982.

Weber 1908: Weber, Heinrich, Lehrbuch der Algebra, 2. ed., Braunschweig, Vieweg, 1896-1908, 3 v.; v. III, 1908.

Wiles 1995: Wiles, Andrew, Modular elliptic curves and Fermat's last theorem, "Annals of mathematics", 141, 1995, pp. 443-551.