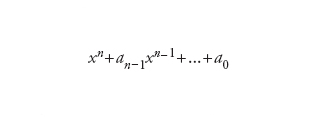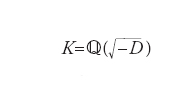campi di numeri
Campi di numeri
Sia α un numero algebrico, cioè un numero complesso che soddisfa un’equazione algebrica p(x)=0, dove p(x) è un polinomio
di grado n≥1 avente coefficienti nel campo ℚ dei numeri razionali. L’insieme K = ℚ[α] di tutte le espressioni polinomiali in α a coefficienti in ℚ è un sottocampo del campo complesso ℂ, detto campo di numeri. Ciò significa che la somma e il prodotto di elementi di K appartengono a K; inoltre, se k è un elemento non nullo di K, −k e 1/k appartengono a K.
Per es., si consideri il numero complesso ζm=cos(2π/m)+i sen(2π/m): ζm soddisfa l’equazione xm−1=0 e il campo di numeri ℚ[ζm] è chiamato m-esimo campo ciclotomico.
Un importante capitolo della teoria algebrica dei numeri si occupa dello studio delle proprietà algebriche e aritmetiche dei campi di numeri. Tale studio coinvolge l’anello OΚ degli interi algebrici di un campo di numeri K, definito come l’insieme degli elementi di K che soddisfano un’equazione p(x)=0 del tipo precedente, dove però si richiede la condizione più restrittiva che i coefficienti di p(x) appartengano all’anello ℤ degli interi relativi. Il fatto che OΚ sia un anello vuol dire che la somma e il prodotto di elementi di OΚ appartengono a OΚ e inoltre l’opposto −k di ogni elemento k di OΚ è ancora un elemento di OΚ .
A titolo di esempio, l’anello degli interi algebrici del campo ciclotomico K=ℚ[ζm] è l’anello ℤ[ζm], contenente tutte le espressioni polinomiali in ζm a coefficienti in ℤ. In particolare, se K è il campo razionale ℚ (ottenuto ponendo m = 1), si ha che OΚ è uguale a ℤ.
Proprietà cruciale nello studio di ℤ è il teorema fondamentale dell’aritmetica, che asserisce che ogni intero positivo n si fattorizza in modo unico (a meno dell’ordine dei fattori) come prodotto di numeri primi: n =p1...pκ (si ricordi che un numero primo p è un intero positivo maggiore di 1 che è divisibile solo per 1 e per sé stesso; dunque p = 2,3,5,7,11,13,...).
Una simile proprietà non vale in generale per l’anello OΚ. La sua corretta generalizzazione, scoperta da Ernst Eduard Kummer, è la seguente. Sia dato un ideale I non nullo di OΚ, cioè un sottoanello non nullo di OΚ con la proprietà aggiuntiva che ogni prodotto ab, con a appartenente a OΚ e b appartenente a I, sia un elemento di I. Un ideale non nullo P di OΚ è detto massimale se P≠OΚ e non esiste alcun ideale I≠OΚ che contenga propriamente P. Si dimostra che ogni ideale non nullo I di OΚ si fattorizza in modo unico (a meno dell’ordine dei fattori) come prodotto di ideali massimali: I =P1...Pκ.
Un campo di numeri K = ℚ[α] è detto estensione di Galois di ℚ se tutte le soluzioni dell’equazione p(x)=0 di grado minimo soddisfatta da α appartengono a K.
In questo caso, si associa a K il suo gruppo di Galois Gal(K/ℚ), costituito dagli automorfismi di K, moltiplicati per mezzo dell’operazione di composizione (un automorfismo di K è una funzione σ:K→K tale che σ(a+b)=σ(a)+σ(b) e σ(ab)=σ(a)σ(b) per ogni scelta di elementi a e b in K).
Per es., l’m-esimo campo ciclotomico ℚ[ζm] è un’estensione di Galois di ℚ e il suo gruppo di Galois è commutativo, isomorfo al gruppo (ℤ/mℤ)× delle unità nell’anello ℤ/mℤ delle classi di resti modulo m.
Il teorema di Kronecker-Weber afferma che ogni estensione di Galois di ℚ, avente gruppo di Galois commutativo, è contenuta in un campo ciclotomico. Dati due campi di numeri K e L, con K contenuto in L, è possibile generalizzare le precedenti definizioni di estensione di Galois e di gruppo di Galois (formulate nel caso K = ℚ). La teoria dei corpi di classe per il campo K classifica tutte le estensioni di Galois di K aventi gruppo di Galois commutativo, dette estensioni abeliane. Un problema fondamentale, detto XII problema di Hilbert, chiede se sia possibile generare le estensioni abeliane di un campo di numeri K per mezzo di funzioni esplicite. Nel caso in cui K è il campo razionale ℚ, il teorema di Kronecker-Weber afferma che questo è possibile per mezzo della funzione esponenziale. Se K=ℚ(√−D), dove D è un intero positivo privo di fattori quadratici, la teoria della moltiplicazione complessa fornisce una risposta affermativa al XII problema di Hilbert, grazie all’uso della teoria delle forme modulari.
Per un campo di numeri generale, il problema è del tutto aperto.