paraboloide
Matematica
Ogni superficie del 2° ordine (quadrica), priva di punti doppi e tangente al piano all’infinito. La prima delle due proprietà esclude tutte le cosiddette quadriche degeneri che comprendono i coni, i cilindri e le quadriche costituite da una coppia di piani distinti o coincidenti; la seconda proprietà mette in luce una stretta analogia (che spiega il termine stesso di paraboloide) esistente tra il paraboloide e la parabola: come la parabola è tangente alla retta all’infinito, così il paraboloide lo è rispetto al piano all’infinito. Di conseguenza il paraboloide è una figura illimitata che può possedere un unico punto all’infinito reale (paraboloide ellittico) o anche una totalità di punti all’infinito reali costituita da due rette improprie (paraboloide iperbolico). Un paraboloide è privo di centro di simmetria; è però dotato in generale di due piani di simmetria ortogonale, detti piani principali che si segano ortogonalmente lungo una retta che è un asse di simmetria. Essa, a sua volta, incontra il paraboloide in un sol punto proprio, detto vertice.
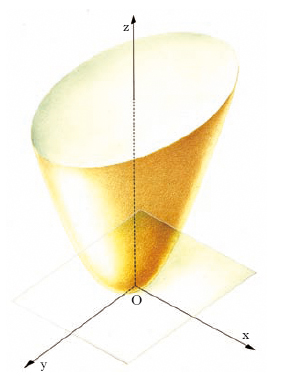
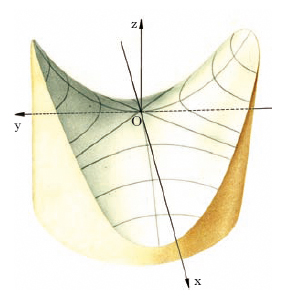
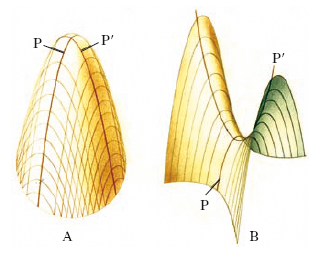
Esistono due tipi di paraboloide; assumendo come piani di riferimento i due piani principali e il piano perpendicolare all’asse nel vertice, le loro equazioni si riducono a una forma particolarmente semplice (forma canonica). Il paraboloide ellittico ha equazione x2/a2+y2/b2=2z (a>0, b>0); esso è segato in ellissi dai piani z=k e in parabole dai piani x=k e y=k; la superficie, dal punto di vista reale, si compone di una sola ‘coppa’, estesa all’infinito, e situata tutta da una stessa banda rispetto al piano a essa tangente nel vertice O (fig. 1); non contiene rette reali. Nel caso particolare a = b si ottiene un paraboloide di rotazione; tutti i piani per l’asse di rotazione sono piani principali. Il paraboloide iperbolico (o a sella) ha equazione x2/a2−y2/b2=2z (a>0, b>0). È a forma di «sella» e si estende all’infinito dall’una e dall’altra banda del piano tangente nel vertice O (fig. 2) che sega la superficie lungo due rette; è una quadrica rigata, contiene cioè due sistemi di rette reali. Tutte le rette di uno stesso sistema, pur essendo sghembe a due a due, sono parallele a uno stesso piano. Tanto il paraboloide ellittico quanto il paraboloide iperbolico sono poi superfici di traslazione: difatti si considerino due parabole P, P′ situate su due piani perpendicolari e aventi lo stesso vertice e lo stesso asse (fig. 3): se una delle due, per es. P, viene sottoposta a una traslazione per cui il suo vertice scorra su P′, la superficie che si ottiene è appunto un paraboloide (ellittico se P e P′ volgono la concavità dalla stessa parte, come in fig. 3A, iperbolico nel caso contrario come in fig. 3B).
Tecnica
In radiotecnica, sono comunemente dette paraboloidi le antenne direttive con riflettori paraboloidici (➔ antenna).