mediana
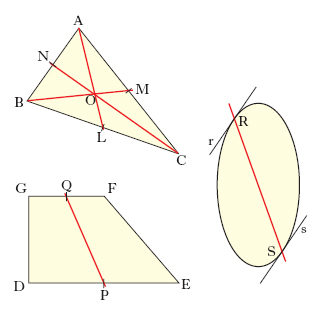
In geometria, la m. di un triangolo è la retta (o anche il segmento) che congiunge un vertice con il punto di mezzo del lato a esso opposto: le tre m. passano per uno stesso punto, che è il baricentro. In fig. AL, BM, CN sono le m. del triangolo ABC. Più in generale, si chiama m. di una figura piana ogni retta che sia asse di simmetria, in generale obliqua, per la figura; così, per es., m. di un trapezio è la retta che congiunge i punti medi delle basi. In fig. QP, m. del trapezio DEFG, è retta di simmetria rispetto alla direzione delle basi DE, FG. M. di una conica è un qualsiasi diametro; in fig., la retta RS è m. per l’ellisse perché è retta di simmetria rispetto alla direzione delle tangenti r, s.
In statistica, m. di una successione (o di una seriazione) finita di valori, disposti in ordine non crescente (o non decrescente), è quel valore che occupa il posto centrale, se il numero dei termini è dispari, o qualunque valore compreso nell’intervallo delimitato dai due termini centrali se il numero dei termini è pari (di solito, si prende il valore centrale di tale intervallo). In generale, indicata con F (x) la funzione di ripartizione della variabile statistica x, se si completa il grafico della funzione negli eventuali punti di discontinuità con segmenti paralleli all’asse delle ordinate, sono valori mediani tutte le radici dell’equazione: F(x)=1/2. La m. soddisfa un’importante condizione di minimo: si dimostra infatti che il valor medio degli scarti (considerati in valore assoluto) rispetto a una costante c raggiunge il suo minimo quando c è un valore mediano.