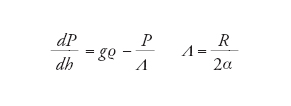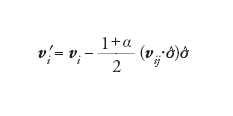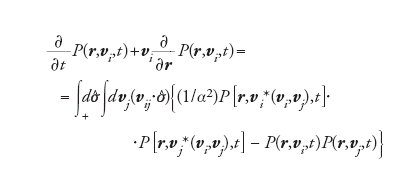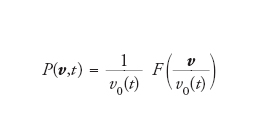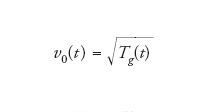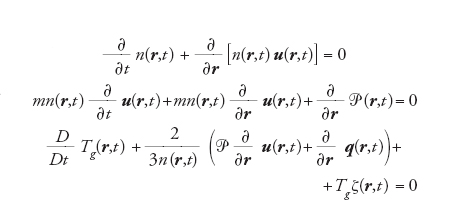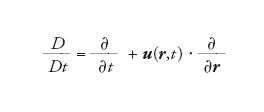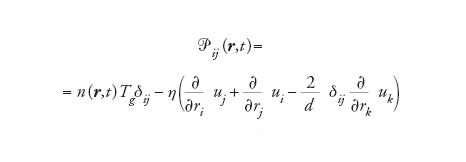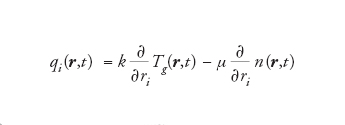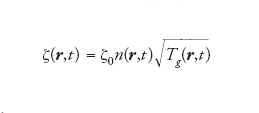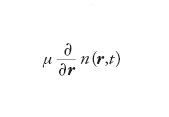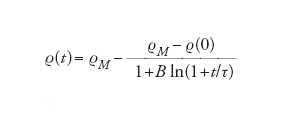Materiali granulari

Materiali granulari

Parliamo di materiali granulari, intendiamo riferirci a sistemi composti da un numero estremamente elevato di particelle macroscopiche. I materiali granulari sono molto comuni, sia nell'ambiente naturale, sia nelle attività quotidiane: lo zucchero, i cereali, il sale, la ghiaia, la sabbia, le polveri, i detriti ne sono esempi particolarmente diffusi. Possiamo affermare che i materiali granulari sono, dopo l'acqua, le sostanze più comuni con cui l'uomo viene a contatto nella sua vita quotidiana. Una loro caratteristica fondamentale è il fatto che le particelle costituenti, per quanto a volte possano essere molto piccole, sono sempre di dimensioni macroscopiche (dell'ordine cioè delle centinaia di μm, dei mm o anche dei cm). Questa proprietà ha conseguenze molto importanti sul comportamento (spesso non intuitivo) di questi sistemi ed è una delle cause principali delle difficoltà che si riscontrano nel costruirne una teoria sistematica e completamente soddisfacente.

Un'altra importante caratteristica dei materiali granulari è che possono essere considerati sistemi a temperatura nulla, in quanto la loro energia tipica è di molti ordini di grandezza maggiore rispetto all'energia termica, pari a k_BT (ove k_B e T sono, rispettivamente, la costante di Boltzmann e la temperatura espressa in kelvin): per esempio, per un granello di dimensione d e massa m si ha una scala di energia pari a mdg (ove g è l'accelerazione di gravità), che è in genere almeno 1012 volte superiore a k_BT (se, per es., consideriamo d=0,1 cm, m=0,01 g e T=300 K). A causa del gran numero di particelle che costituiscono un materiale granulare, potrebbe sembrare naturale applicare a questi sistemi la meccanica statistica, considerando come costituenti elementari i grani; tuttavia, poiché questi ultimi sono di dimensioni macroscopiche, le loro interazioni sono dissipative (vale a dire che l'energia, a livello macroscopico, non si conserva) e questo rende molto più difficile applicare loro le metodologie usate con successo nello studio dei gas e dei liquidi.

Questa difficoltà si riscontra a dispetto del fatto che i mezzi granulari sono apparentemente molto simili ai sistemi per i quali la meccanica statistica contribuisce a una descrizione fisica esauriente, come appunto i gas e i liquidi. La sabbia e l'acqua hanno molte analogie (per es., la sabbia scorre come un liquido e, come questo, può riempire una bottiglia e fuoriuscirne), pur mostrando grandi differenze. Analogamente, i materiali granulari hanno comportamenti peculiari nei processi di mescolamento. Se consideriamo infatti due gas (o liquidi) diversi, inizialmente separati da un setto, notiamo che una volta rimossa la parete che li divide si ha un rapido mescolamento, al termine del quale diventa praticamente impossibile separare nuovamente i due gas. Al contrario, due polveri diverse, se ben miscelate, possono essere comunque separate facendo vibrare opportunamente il recipiente che le contiene, mentre il loro mescolamento è assai difficile da realizzare, come è ben noto in quei settori, come l'industria farmaceutica, nei quali questo processo riveste un grande interesse applicativo.

Proprietà statiche

In un recipiente (per semplicità un cilindro di raggio R) pieno d'acqua (o, più in generale, di un fluido newtoniano di densità ϱ) fino a una quota h, la pressione sul fondo è data dalla legge di Stevino:

[1] P(h) = ϱgh.

A causa del grande numero di molecole del liquido, in contenitori di dimensioni macroscopiche non si hanno, rispetto a questo valore, apprezzabili fluttuazioni di pressione. In un recipiente pieno di sabbia (o più in generale di un materiale granulare, come cereali o ghiaia), la pressione cresce invece con la quota soltanto se h non è molto grande rispetto a R, mentre per grandi valori di h la pressione rimane costante. Questo fenomeno, noto come legge di Janssen, è alla base del funzionamento delle clessidre: il flusso della sabbia attraverso il foro è costante, indipendentemente da quanta ne sia rimasta nella zona superiore del contenitore.

La spiegazione fenomenologica di quanto avviene è la seguente. Consideriamo un disco di spessore dh di materiale granulare e indichiamo con dP la variazione di pressione tra le quote h e h+dh; in situazioni di equilibrio, la forza di gravità πR²gϱdh sarà bilanciata dal termine di pressione πR²dP e dalla forza di attrito sulla parete 2πRP_adh, dove P_a è il contributo di pressione dovuto all'attrito stesso. Janssen assume che P_a sia proporzionale a P: P_a=αP, ove α è un coefficiente adimensionale che dipende dalla natura del materiale granulare (e dalle caratteristiche della parete). Si ha quindi

[2] πR²gϱdh = πR²dP + 2πRαPdh

da cui

[3] formula.

La soluzione dell'equazione precedente è immediata. Imponendo l'ovvia condizione P(0)=0, si ha

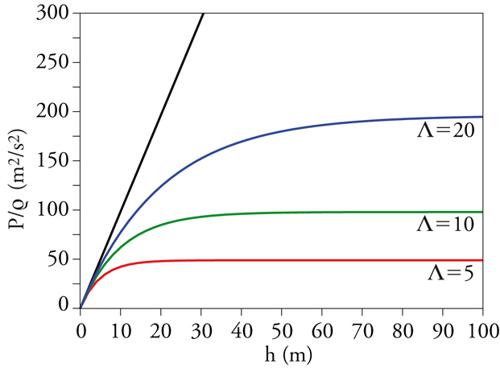
[4] P(h) = Λgϱ(1− e^−h/Λ).

fig. 2

Si noti che se h è molto minore di Λ si ha nuovamente la legge di Stevino, mentre quando h è molto grande rispetto a Λ, la pressione raggiunge il valore limite Λgϱ (fig. 2). Possiamo quindi affermare che la pressione sul fondo è determinata dal solo materiale nello strato di spessore ∼Λ più vicino al fondo, mentre la materia granulare a maggiore distanza non vi contribuisce.

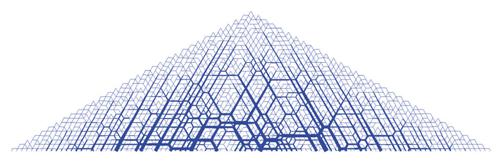
Il meccanismo microscopico responsabile di tale comportamento è la formazione di archi (o, meglio, volte) costituiti da strutture composte da grani che (proprio come negli archi delle costruzioni) scaricano la pressione sulle pareti laterali. La posizione e il numero di queste strutture sono casuali; vale a dire che, svuotando il contenitore e riempiendolo nuovamente, le volte si formeranno in numero e posizioni diverse. Inoltre, sia sul fondo sia sulle pareti laterali la pressione è distribuita in modo molto disomogeneo ed è molto grande nei punti dove le volte toccano, piccola dove non toccano. Nonostante l'elevato numero di grani in un recipiente macroscopico (per es., un chilogrammo di cereali contiene ≈10⁴÷10⁵ grani e in un silo di 100 m³ si hanno ≈10⁹÷10¹⁰ grani), le fluttuazioni di pressione sono molto grandi. Questo fenomeno, dovuto alla formazione degli archi e assente nei contenitori di liquidi newtoniani, ha effetti molto spettacolari ‒ e purtroppo negativi ‒ sulla stabilità dei silos, che esplodono con relativa facilità (soltanto negli Stati Uniti, si verificano all'icirca 1000 esplosioni l'anno).

Il motivo sostanziale di questo comportamento atipico è il seguente: a causa degli archi, il sistema granulare nel silo si comporta come se fosse composto da poche particelle equivalenti, corrispondenti ai blocchi (di dimensioni ∼Λ) di materiale tra le volte. In un contenitore cilindrico di raggio R e altezza L, il numero di questi blocchi non è mai troppo grande e vale ∼L/R, ossia ∼L/Λ. Poiché questo numero non può divenire elevato, la pressione non ha una distribuzione approssimativamente gaussiana con piccole fluttuazioni, come nei gas e nei liquidi. Studi sperimentali, in accordo con modelli semplificati (in cui si fa riferimento a sferette rugose), mostrano che, sul fondo di un recipiente contenente materiali granulari, i grani esercitano una forza f la cui densità di probabilità è data da

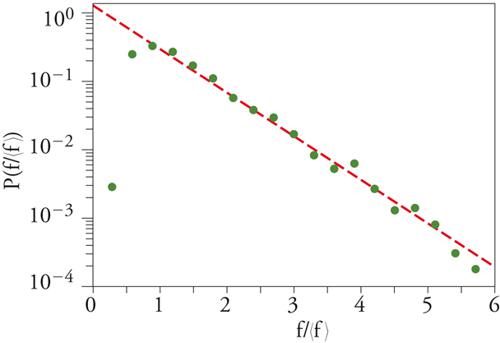
[5] P(f) = ce^−f/f₀ ,

3

4

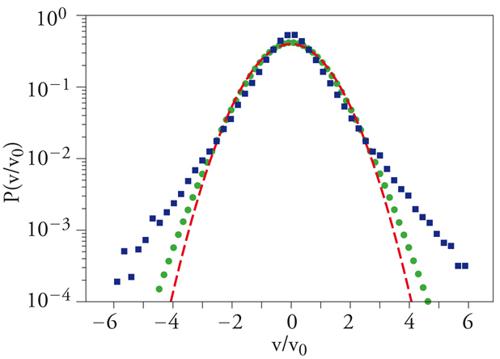
dove c e f₀ sono costanti che dipendono dalle dimensioni del contenitore e dal tipo di granuli. Si ha quindi che le fluttuazioni sono O(1), invece di essere O(1/√N) come nei comuni liquidi (dove N è il numero di componenti microscopiche). Inoltre, le code della P(f) sono molto più popolate di quelle di una variabile gaussiana con lo stesso valore medio e la stessa varianza, come risulta dalle figg. 3 e 4.

Proprietà dinamiche

In presenza di sollecitazioni esterne, i materiali granulari possono comportarsi in modi diversi. Si può pertanto parlare di gas, liquidi e talvolta persino di vetri granulari a seconda del grado di ordine presente nel fluido. Nello studio teorico dei fluidi granulari si osserva un interesse per la cinetica degli stati gassosi, definiti come quegli stati per cui è possibile una descrizione basata su un'equazione di Boltzmann modificata. In questo caso è infatti possibile ripercorrere il programma classico della meccanica statistica e della teoria cinetica, ottenendo molte analogie e alcune profonde differenze rispetto ai gas molecolari. Il modello fondamentale alla base della cinetica granulare è il gas di N sfere dure e lisce (al posto delle sfere si hanno dischi in due dimensioni o barrette in una dimensione), anelastiche, di diametro σ e massa m in un contenitore di volume V, solitamente cubico, di lato L e con condizioni periodiche al contorno. Ogni sfera è caratterizzata da una posizione r_i e da una velocità v_i.A contatto, quando cioè ∣r_i−r_j∣=σ, le sfere i e j si urtano conservando la propria quantità di moto e dissipando una frazione dell'energia cinetica; si ha

[6] formula,

dove v_i′ indica la velocità della sfera i dopo la collisione con la sfera j, v_ij=v_i−v_j, σ^{^} è il vettore unitario che unisce i centri delle due sfere e α∈[0, 1]. In un gas granulare è naturale definire, come nella cinetica dei gas, una temperatura granulare T_g=2〈E〉/dN, dove d è la dimensione dello spazio ed E è l'energia cinetica. Se si ha uno stato statisticamente stazionario, la media 〈f〉 è da intendersi come una media temporale, altrimenti è necessaria una media a tempo fissato su molte copie del sistema.

Nel limite di Grad-Boltzmann (N→∞, e σ→0, con Nσ² costante) e con l'ipotesi di caos molecolare, cioè considerando scorrelate due sfere prima dell'urto, è possibile scrivere un'equazione di Boltzmann:

[7] formula

in cui P(r,v_i,t) è la densità di probabilità di trovare una sfera in posizione r con velocità v_i al tempo t; v_i*(v_i,v_j), v_j*(v_i,v_j) sono le velocità delle particelle 1 e 2 rispettivamente, prima di una collisione che le trasformi in v_i, v_j (si ottengono invertendo la regola di collisione [6]); infine ∫₊dσ^{^} indica un'integrazione sugli angoli di collisione con il vincolo che v_ij∙σ^{^}>0.

La [7] è simile all'equazione di Boltzmann usuale, a parte il fattore 1/α² dovuto alla dissipazione nella collisione che moltiplica il termine di guadagno dell'integrale sulle collisioni. Un gas granulare non soggetto a un'azione esterna non raggiunge uno stato di equilibrio statistico, ma evolve fino a esaurire tutta la propria energia. Se si prepara il gas in una configurazione omogenea, con le posizioni e le velocità delle sfere scelte a caso tra le configurazioni tipiche di equilibrio di un gas elastico, è possibile supporre l'esistenza di un regime detto di raffreddamento omogeneo, in cui le posizioni restano distribuite omogeneamente nello spazio, mentre le velocità hanno una distribuzione che evolve nel tempo con una legge del tipo

[8] formula

con

[9] formula.

fig. 5

Durante il raffreddamento omogeneo, la temperatura decresce secondo la legge di Haff T_g(t)=T_g(0)(1+t/τ)⁻², con una costante τ che dipende dalla densità e dalla temperatura al tempo 0 e da α, mentre la distribuzione F(c) è diversa dalla classica distribuzione di Maxwell-Boltzmann e presenta code più popolate, con andamento asintotico esponenziale (fig. 5).

Uno studio di stabilità del regime di raffreddamento omogeneo mostra che lo stato omogeneo è stabile se la dimensione linerare L del sistema è inferiore a una dimensione critica L_c(α), altrimenti è instabile e una fluttuazione può condurre il sistema a un regime non omogeneo. In particolare, il modo di shear (gradiente di velocità trasversale) è il primo ad amplificarsi, producendo strutture vorticose e innescando in un secondo tempo forti eterogeneità nella densità del gas. Si osserva la formazione di ammassi estremamente densi, detti clusters, e in alcune situazioni emerge una singolarità della dinamica chiamata collasso anelastico: alcune sfere rimangono intrappolate in una sequenza di collisioni infinita in un tempo finito, analoga alla sequenza di rimbalzi di una sfera anelastica lasciata cadere al suolo da una certa altezza. Il modello di gas granulare libero fin qui descritto è importante per una costruzione rigorosa di un'idrodinamica granulare, ma risulta molto lontano dalla realtà: negli esperimenti è necessario fornire energia al gas in modo da ottenere uno stato statisticamente stazionario.

Una modellizzazione di situazioni reali deve necessariamente contenere una sorgente esterna di energia che, negli esperimenti più semplici, è l'agitazione del contenitore o di una delle sue pareti. L'immissione di energia ai bordi del sistema implica un regime stazionario non omogeneo, con flussi di materia ed energia che attraversano l'intero volume. In alcuni casi questo modo di fornire energia conduce a regimi che non sono descrivibili idrodinamicamente, per via delle grandi fluttuazioni spaziali e temporali. Per ottenere un regime omogeneo e stazionario è necessario assicurarsi che l'energia raggiunga omogeneamente tutte le componenti del sistema. Una situazione simile si può raggiungere negli esperimenti attraverso la cosiddetta fluidificazione con un gas (anche semplice aria) in cui, per raggiungere ogni singolo grano, un forte getto è spinto attraverso il materiale. Nei modelli questo meccanismo viene riprodotto con termini stocastici che agiscono su ogni particella. Lo studio di questi modelli mostra ancora una volta la presenza di distribuzioni di velocità non maxwelliane, con un aumento di probabilità per le velocità grandi. Anche in presenza di un'iniezione omogenea di energia, l'anelasticità delle collisioni può condurre il sistema a regimi stazionari spazialmente non omogenei, con la presenza di clusters frattali.

Idrodinamica granulare

La costruzione di una teoria idrodinamica per un fluido granulare può avvenire attraverso due strade. Una, di tipo fenomenologico, parte dall'osservazione dell'esistenza, in quasi tutte le situazioni sperimentali, di una scala di descrizione del sistema in cui i cambiamenti avvengono in media molto più lentamente rispetto al livello cinetico dei singoli voli liberi e degli urti tra particelle. In analogia con i fluidi classici, a questa scala è quindi naturale scrivere alcune equazioni di conservazione e di bilancio per i campi di massa, di quantità di moto e di energia. Queste equazioni non sono chiuse fin quando i flussi che compaiono al loro interno non sono dati in funzione dei tre campi, e tale chiusura viene fatta sulla base di assunzioni arbitrarie e di osservazioni sperimentali. Questo modus operandi, già poco utile nel contesto dei fluidi molecolari in quanto privo di universalità e di riproducibilità, diventa ancora meno praticabile quando applicato a un fluido granulare, per il quale le situazioni anomale (ossia di rottura dell'idrodinamica) sono molto più comuni; è quindi imprescindibile una conoscenza rigorosa dei limiti di validità della descrizione stessa, che parta da principî primi. In molte situazioni semplici è infatti possibile mostrare che, in un gas di particelle anelastiche, il cammino libero medio e il tempo di volo libero tra due urti possono fluttuare fortemente e diventare paragonabili alle scale spaziali e temporali macroscopiche (si dice che un fluido granulare può avere alti numeri di Knudsen).

La seconda strada, che è più rigorosa e permette un miglior controllo della validità dei risultati, è quella di procedere a partire dall'equazione di Boltzmann. Una procedura seguita con successo è quella, anche detta metodo di Chapman-Enskog, in cui si effettua uno sviluppo della distribuzione P(r,v,t), così come dei suoi gradienti spaziali e temporali, usando come parametro piccolo il numero di Knudsen, ovverosia il rapporto tra cammino libero medio e lunghezza caratteristica delle variazioni spaziali. I limiti di validità di tale descrizione appaiono nel troncamento di questo sviluppo. L'ordine zero corrisponde all'equazione per il raffreddamento omogeneo, di cui si è parlato precedentemente. Al primo ordine si ottengono le equazioni idrodinamiche granulari di Navier-Stokes (ovvero i flussi sono funzioni lineari dei gradienti):

[10] formula

dove si è indicata la derivata sostanziale con

[11] formula

e in cui n, u e T_g sono rispettivamente i campi di densità numerica, velocità e temperatura granulare, mentre

[12] formula

è il tensore di pressione (con η viscosità di taglio), e

[13] formula

è il flusso di calore (con k conducibilità termica e μ un nuovo coefficiente di trasporto), e

[14] formula

è il cosiddetto tasso di raffreddamento. I coefficienti η, k, μ, ζ₀ sono funzioni dei parametri del sistema. Rispetto alle usuali equazioni di Navier-Stokes, nel flusso di calore sono presenti i termini T_gζ, che rappresenta la dissipazione di energia interna dovuta alle collisioni, e

[15] formula

proporzionale al gradiente di densità.

Tali equazioni descrivono in modo soddisfacente i fluidi granulari a densità sufficientemente basse, condizione che in genere implica α vicino a 1 e sollecitazioni esterne non troppo intense. Esse sono importanti per lo studio delle instabilità osservate sperimentalmente: in particolare, l'analisi di stabilità lineare con condizioni al contorno simili a quelle di un contenitore verticale agitato ha mostrato l'esistenza di fenomeni di convezione, di onde di densità trasversali nel volume e sulla superficie e, nel caso di miscele di differenti tipi di grani, di fenomeni di segregazione delle diverse componenti. L'esistenza di un regime idrodinamico, sebbene ristretto a situazioni diluite, sottintende la possibilità di descrivere in maniera lineare i fenomeni di trasporto, come la diffusione della massa o del calore e la validità di ben definite relazioni tra la risposta a una sollecitazione esterna e le fluttuazioni del sistema in assenza della sollecitazione: in meccanica statistica dei sistemi fuori equilibrio si parla di relazioni di fluttuazione-dissipazione. Per stati di raffreddamento omogeneo, quindi in regime non stazionario, è stata ipotizzata e verificata numericamente la validità delle relazioni di fluttuazione-dissipazione con termini aggiuntivi rispetto alla relazione classica. In stati stazionari omogenei è stata verificata numericamente la validità delle relazioni di fluttuazione-dissipazione usuali, con una sola variante: al posto della temperatura esterna, nelle relazioni compare la temperatura granulare, che è in genere minore. Questo fa sì che, per esempio, a parità di mobilità il coefficiente di diffusione in un gas granulare sia più piccolo che non in un gas reale.

In tutte le situazioni di densità e sollecitazione esterna intermedie tra quella dei fluidi granulari diluiti e quella dei materiali granulari completamente a riposo, si osservano i cosiddetti regimi plastici o vetrosi. Sono situazioni in cui l'evoluzione è fortemente influenzata dall'intera storia del sistema e dalle sue condizioni al contorno. Le due configurazioni più comuni in cui questo tipo di regime è studiato sono il cosiddetto tapping, ovverosia una sequenza alternata di intervalli di assestamento in presenza di sola gravità e brevi intervalli di sollecitazione (vibrazioni), e lo shear, cioè l'applicazione di sforzi di taglio in geometrie cilindriche o cubiche. Nel tapping il fenomeno più evidente è il rilassamento estremamente lento della densità media del sistema, che impiega tempi lunghissimi per convergere a uno stato asintotico ϱ_M:

[16] formula

in cui B e τ dipendono dal mezzo granulare, dalla frequenza e dall'intensità della vibrazione. Una volta che i grani sono stati gettati nel contenitore, e dopo ogni successiva vibrazione, il sistema si ferma in uno stato stabile che non corrisponde al minimo assoluto di energia. La densità non è la massima ϱ_M corrispondente all'impacchettamento ottimale, a causa di difetti spaziali da eliminare con l'aumento della densità.

Questa fenomenologia è ben riprodotta da modelli in cui il sistema può restare intrappolato in minimi locali (stati bloccati), il cui insieme domina la dinamica nel limite termodinamico (ipotesi di Edwards): con l'aumentare della densità, per uscire da ognuno di questi minimi il sistema deve modificare la propria configurazione su scale sempre maggiori, secondo un meccanismo di invecchiamento simile a quello dei sistemi disordinati, come i vetri di spin o i vetri strutturali. Negli esperimenti di shear, invece, il fenomeno dominante è la formazione, vicino alla parte del contenitore che applica lo sforzo, di una striscia fluida, dello spessore di pochi grani, quasi del tutto separata dal resto del sistema, che resta invece a riposo. La formazione di una striscia fluida appare negli esperimenti di cumuli di sabbia, in cui la superficie inclinata è libera e lo scivolamento di valanghe dovute all'aggiunta di nuovo materiale sulla cima del cumulo avviene su uno strato di pochi grani di spessore.

Bibliografia

Baldassarri 2005: Baldassarri, Andrea e altri, What is the temperature of a granular medium?, "Journal of physics: condensed matter", 17, 2005, pp. S2405-S2428.

Brey 1998: Brey, J. Javier e altri, Hydrodynamics for granular flow at low density, "Physical review E", 58, 1998, pp. 4638-4653.

Cercignani 1975: Cercignani, Carlo, Theory and application of the Boltzmann equation, New York, Elsevier, 1975.

De Gennes 1998: de Gennes, Pierre-Gilles, Reflections on the mechanics of granular matter, "Physica A", 261, 1998, pp. 267-293.

Duran 2000: Duran, Jacques, Sands, powders, and grains, Berlin, Springer, 2000.

Jaeger 1996: Jaeger, Heinrich - Nagel, Sidney R. - Behringer, Robert P., Granular solids, liquids and gases, "Review of modern physics", 68, 1996, pp. 1259-1273.

Kadanoff 1996: Kadanoff, Leo P., Built upon sand: theoretical ideas inspired by granular flows, "Review of modern physics", 71, 1996, pp. 435-444.

Pöschel, Luding 2001: Granular gases, edited by Thorsten Pöschel, Stefan Luding, Berlin, Springer, 2001.