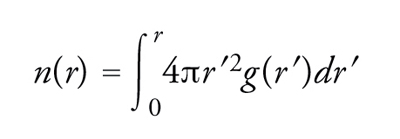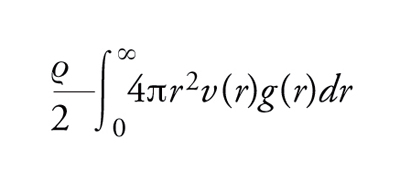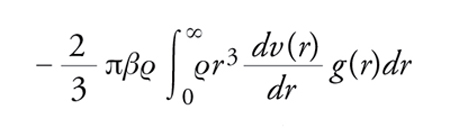Liquidi

Liquidi

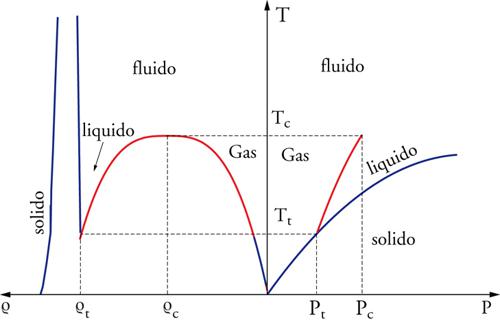
Gli stati gassoso, liquido e solido (cristallino) sono le tre forme in cui si presenta la materia in equilibrio termodinamico: lo stato gassoso è caratterizzato da bassa densità e da assenza di ordine nella posizione spaziale di atomi e molecole, quello solido è contraddistinto da alte densità e ordine su grandi distanze, mentre lo stato liquido ha densità confrontabili con quelle del solido, ma presenta un ordine limitato a distanze atomiche o molecolari. Delle tre forme è osservabile quella con energia libera minore, e ciò dipende dalle variabili termodinamiche temperatura T, pressione P e volume V (o densità ϱ): a bassa pressione, esistono in equilibrio i soli stati gassoso (alta temperatura) e solido (bassa temperatura); per pressioni maggiori e temperature intermedie, tra la fase solida e quella gassosa si inserisce la fase liquida; a pressioni o temperature che superano valori critici (P_c, T_c), le fasi liquida e gassosa divengono indistinguibili.

A differenza delle fasi solida e gassosa, presenti anche in particelle soggette a sole forze repulsive, lo stato liquido è intimamente connesso con l'esistenza di forze di attrazione tra atomi o molecole. Se rappresentiamo un sistema di N particelle utilizzando come scale di energia e di distanza, rispettivamente, l'intensità ε e il raggio di azione σ dell'attrazione tra particelle, lo stato liquido è caratterizzato da una temperatura ridotta k_BT/ε e da una densità ridotta Nσ³/V (con k_B costante di Boltzmann) entrambe uguali circa a 1; ciò indica che l'energia cinetica (∼k_BT) è confrontabile con l'energia potenziale (∼ε) e che le particelle riempiono il volume.

fig. 1

Il diagramma di fase di una sostanza tipica (fig. 1) evidenzia, nei piani (ϱ, T) e (P, T), le porzioni in cui le differenti fasi sono osservabili: la fase liquida è confinata in una piccola regione, delimitata sull'asse T dalla temperatura critica T_c, che rappresenta la temperatura più alta a cui liquido e gas sono formalmente distinguibili, e dalla temperatura T_t del punto triplo, in cui la fase liquida coesiste con le fasi solida e gassosa. La condensazione dello stato liquido durante il raffreddamento isobaro di un gas nell'intervallo P_t〈P〈P_c trae origine dalla stabilizzazione energetica associata alla formazione di aggregati di particelle, con alta densità locale, che compensa la perdita di entropia traslazionale. Un ulteriore raffreddamento sotto la temperatura di solidificazione genera la cristallizazione del liquido, e in questo stato l'ulteriore diminuzione dell'energia potenziale del sistema è compensata dalla perdita di entropia associata all'ordinamento delle posizioni relative delle particelle su grandi distanze.

Lo studio della maggior parte delle proprietà dei liquidi fa riferimento alla fisica classica, in quanto lo stato liquido in equilibrio esiste soltanto molto al di sopra di T_t, temperatura alla quale la lunghezza d'onda di de Broglie λ_B è il più delle volte assai minore della distanza interatomica. Restano esclusi da questo schema i liquidi di atomi particolarmente leggeri, quali l'idrogeno (che ha massa molto piccola), il neon (piccola massa e T_t ridotta) e l'elio (che è liquido fino alla temperatura nulla, nel cui limite λ_B→∞): per essi λ_B è almeno dello stesso ordine di grandezza delle distanze interatomiche.

classificazione

L'interazione microscopica tra le particelle costituenti è alla base del comportamento macroscopico della materia. Comprendere lo stato liquido significa quindi predire proprietà termodinamiche, strutturali e dinamiche partendo dal potenziale di interazione tra atomi e molecole e dal modo in cui esso determina il comportamento collettivo. Questo approccio suggerisce di classificare i liquidi in base alla forma assunta dal potenziale di interazione. Tale criterio consente di raggruppare i diversi materiali in categorie, i cui componenti godono, nello stato liquido, di proprietà fisiche simili. Tra le classi più rilevanti troviamo: (a) liquidi soggetti a potenziali a simmetria radiale composti da una regione attrattiva e una repulsiva assai ripida. Un tipico esempio è il potenziale di Lennard-Jones V(r)=4ε[(σ/r)¹²−(σ/r)⁶], che modellizza sia il contributo di repulsione tra gli elettroni dei gusci esterni mediante la potenza r⁻¹², sia il contributo attrattivo di forze di dispersione di dipolo indotto, attraverso la dipendenza r⁻⁶; in questo gruppo, dei cosiddetti liquidi semplici, sono inclusi gli stati liquidi dei gas rari (Ar, Kr) e quelli di molecole con struttura essenzialmente sferica, come CH₄; (b) liquidi in cui agiscono potenziali a simmetria radiale dotati di una componente repulsiva e di una attrattiva a lungo raggio, generata da interazioni di Coulomb; vi rientrano i metalli fusi, per esempio Na e Hg. La forma esplicita dell'interazione tra gli ioni dipende fortemente dalla presenza del gas di elettroni di conduzione. In questi sistemi, il potenziale efficace che modellizza l'interazione tra coppie di particelle, calcolato sotto opportune approssimazioni, suggerisce che la regione attrattiva sia caratterizzata da una coda oscillante a lungo raggio. I parametri del potenziale efficace dipendono sensibilmente dalla densità del liquido; (c) sistemi ionici, che si differenziano dalla categoria precedente per l'assenza di schermo delle interazioni elettrostatiche e per essere elettricamente neutri su scala locale. Esempi di tali sistemi, nei quali i fenomeni di polarizzazione possono essere importanti, sono i sali fusi, come NaCl; (d) liquidi polari, nel cui potenziale di interazione sono presenti momenti di dipolo o di multipolo elettrici, come HBr, H₂, N₂; (e) liquidi associati, in cui è presente una forte interazione specifica direzionale (per es. legame idrogeno), come acqua e glicerolo.

Di seguito sono analizzate le proprietà essenziali dello stato liquido, con riferimento alla prima di queste classi e nell'ambito della fisica classica. Le principali differenze tra i liquidi classici e quelli quantistici originano dalla non commutatività delle posizioni e dei momenti e dagli effetti di scambio dovuti alla statistica ‒ di Bose-Einstein oppure di Fermi-Dirac ‒ a cui obbediscono le particelle (atomi e molecole). Tali differenze si osservano sia nelle proprietà termodinamiche, sia in quelle strutturali, misurabili per esempio in esperimenti di diffusione, che campionano la natura ondulatoria della funzione d'onda.

Proprietà statiche: struttura e termodinamica

fig. 2

La fig. 2 mostra tre configurazioni caratteristiche di una tipica sostanza monoatomica, per esempio l'argon, nelle tre diverse fasi, gassosa, liquida e cristallina. Nello stato liquido, la densità è simile a quella dello stato cristallino, ma ben diversa è la posizione relativa degli atomi, non ordinata nello spazio: ogni atomo è circondato da una disposizione spaziale di vicini differente. Questa diversità locale, che si esprime in termini di disordine, è l'elemento caratterizzante dello stato liquido e allo stesso tempo la causa delle difficoltà di una sua modellizzazione teorica. Proprio il disordine locale è infatti responsabile dell'assenza per i liquidi di una configurazione limite di riferimento che sia risolubile esattamente, rappresentata per i gas dal modello del gas ideale, in cui vi è assenza totale di ordine spaziale, e per i solidi dal modello di cristallo armonico, in cui vi è completo ordine spaziale.

La presenza di disordine nelle posizioni atomiche rende necessaria una trattazione statistica. Al livello più elementare, la quantizzazione dell'ordinamento nello stato liquido è effettuata per il tramite della funzione di distribuzione di coppia g(r), che fornisce una misura della probabilità, normalizzata rispetto a una distribuzione completamente casuale, di trovare un qualsiasi atomo a una distanza compresa tra r e r+dr da un altro atomo scelto a caso. Il numero medio n(r) di atomi contenuti in una sfera di raggio r, il cui centro coincida con la posizione di un atomo arbitrario, può essere scritto in termini di g(r) come

[1] formula.

fig. 3

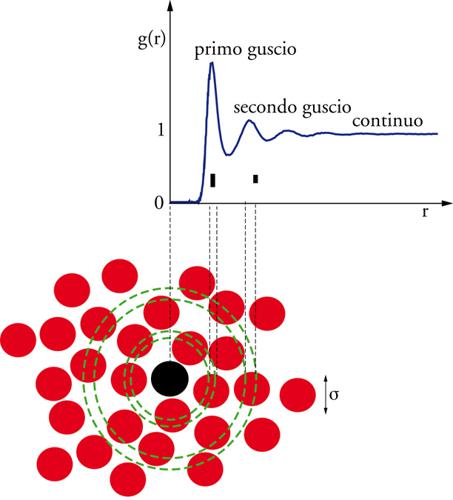
In prima approssimazione, la struttura di un liquido può considerarsi caratterizzata qualora siano note la funzione di distribuzione di coppia e la sua dipendenza dalla temperatura e dalla pressione. La forma tipica di g(r) per un liquido atomico è mostrata in fig. 3. La probabilità di trovare coppie di particelle molto vicine tra loro è nulla ‒ g(r)=0 ‒ a causa della componente repulsiva del potenziale a piccole distanze, che determina il cosiddetto volume escluso. La probabilità di trovare un vicino presenta un massimo intorno alla distanza σ in cui il potenziale di interazione tra gli atomi ha un minimo; una serie di oscillazioni smorzate, con periodicità σ, suggerisce che nel liquido si realizzi una struttura a gusci concentrici. John D. Bernal e G.D. Scott, a metà del secolo scorso, ipotizzarono che la struttura dei liquidi è essenzialmente determinata dalla parte repulsiva del potenziale, che impone un forte vincolo sulla distanza minima tra gli atomi (mentre la parte attrattiva è in prima approssimazione responsabile della sola energia di coesione). Secondo questa ipotesi, informazioni sul random packing (impacchettamento casuale) di oggetti impenetrabili (nel caso specifico sfere) potevano essere utilizzate per predire la forma della funzione di distribuzione di coppia, trasformando il calcolo della g(r) in un problema con forte valenza matematica e statistica.

L'ipotesi di Bernal ha trovato numerose conferme ed è alla base della ricerca svolta negli ultimi cinquanta anni. Il modello teorico di sfere dure, ossia particelle impenetrabili di diametro σ, è risolubile analiticamente con opportune approssimazioni e in modo esatto mediante simulazioni numeriche. È divenuto il modello di riferimento per calcolare le proprietà dei liquidi semplici con metodi perturbativi, pur essendo un modello atermico, in cui la temperatura è irrilevante, e non prevedendo, poiché il potenziale è privo di qualsiasi componente attrattiva, uno stato liquido, ma soltanto uno stato fluido che dipende dalla frazione di volume η occupata.

Le teorie perturbative si basano sulla possibilità di separare il potenziale v(r) in una parte v₀(r) di riferimento e in una w(r) di perturbazione: l'energia libera del liquido è dunque esprimibile come somma di quella delle sfere dure e di un contributo perturbativo, che al primo ordine è il valore medio di w(r) calcolato sul sistema imperturbato. Per esempio, l'energia libera proposta da Johannes Diderik van der Waals nel 1867 può essere ricavata nello schema perturbativo assumendo per le sfere dure un'equazione di stato approssimata del tipo βP/ϱ=1/(1−4η), con β=1/(k_BT), corretta soltanto per piccoli valori di η, e una perturbazione attrattiva w costante, infinitesima, ma di raggio d'azione infinito (Kac model), che aggiunge a βP/ϱ il contributo −βϱa, con a costante positiva.

La funzione di distribuzione di coppia riveste un ruolo centrale nello studio dei liquidi, sia perché offre una misura della loro struttura sia perché, nel caso di potenziali di interazione di coppia v(r), permette di calcolare diverse quantità termodinamiche e la stessa equazione di stato, che lega P, T e V. L'energia potenziale per una particella è infatti calcolabile come

[2] formula

e il contributo alla pressione, in eccesso rispetto alla componente cinetica che si ha anche in assenza di interazioni, come

[3] formula.

Per questi motivi, per quel che concerne la struttura statica, la teoria dei liquidi è essenzialmente finalizzata al calcolo della g(r) una volta noti il potenziale di interazione, la temperatura e la densità.

Accanto alle tecniche perturbative, nello studio della struttura dei liquidi sono stati sviluppati approcci teorici differenti da quelli utilizzati nello studio dei solidi e dei gas. Il punto di partenza è l'equazione esatta di Ornstein-Zerniche (OZ), che lega la g(r) alla cosiddetta funzione di correlazione diretta c(r). Sebbene g(r) e c(r) formalmente siano definite entrambe da sviluppi 'diagrammatici', la relazione formale tra c(r) e g(r) non è trattabile analiticamente. Le teorie integrali dei liquidi si basano dunque su approssimazioni (dette chiusure) per la funzione c(r) scritta come funzione della g(r) e del potenziale v(r), al fine di trasformare l'equazione di OZ in un'equazione per la sola g(r) risolvibile analiticamente (in casi molto limitati) o numericamente. Tra le prime a essere state utilizzate troviamo le approssimazioni di Percus-Yevich, quelle di catena iperconnessa (hypernetted chain) e quelle di Debye-Hückel. Oggi si tende a preferire chiusure più sofisticate, che, sebbene siano risolubili soltanto numericamente, sono coerenti con la termodinamica e garantiscono una migliore descrizione della struttura del liquido; una strada di più recente sviluppo è basata sulla teoria del funzionale densità, un'espressione dell'energia libera del fluido in presenza di disomogeneità spaziali. In entrambi gli approcci, la validità delle approssimazioni è verificata confrontando le predizioni teoriche con la g(r) misurata sperimentalmente, o calcolata per il tramite di simulazioni numeriche del modello. Uno dei modi possibili per misurare g(r) è mediante esperimenti di diffrazione di raggi X e neutroni, in cui si analizza la radiazione diffusa da un campione illuminato da un fascio monocromatico e si ottiene una misurazione diretta del cosidetto fattore di struttura S(q), trasformata di Fourier della g(r).

Lo sviluppo delle equazioni integrali e delle teorie perturbative ha essenzialmente risolto per la classe dei liquidi semplici, in cui agiscono potenziali a simmetria radiale con raggio di interazione finito, la questione di come trattare l'equilibrio in termini di meccanica statistica con riferimento a proprietà termodinamiche e strutturali, mentre resta ancora aperto il problema per i liquidi associati, i cui potenziali di interazione non hanno simmetria radiale, e per i liquidi molecolari e macromolecolari. Nei liquidi associati, il numero di coordinazione medio, ossia il numero di primi vicini, è spesso minore di sei. Per questi sistemi, il modello di sfere dure non rappresenta un riferimento adeguato, in quanto la g(r) assume un valore notevolmente diverso da quello dei liquidi semplici. La maggior parte delle teorie integrali fallisce nel predire la struttura di questi liquidi in condizioni in cui il reticolo di legami direzionali è esteso. Componenti eccellenti di questa classe di liquidi sono l'acqua e la silice (SiO₂). Nel caso dell'acqua, l'interazione direzionale è dovuta al legame idrogeno, cui è associata un'energia di circa 2,5 kJ/mol, intermedia tra quella tipica delle interazioni dipolari e quella delle interazioni covalenti. La presenza di due protoni per ogni molecola d'acqua porta al realizzarsi di una coordinazione tetraedrica nel sistema. Nel caso dell'SiO₂, l'interazione è di natura elettrostatica e, sebbene a livello ionico le interazioni possano essere assunte come a simmetria radiale, la struttura risultante degli ioni di Si è fortemente tetraedrica. L'interazione direzionale e la correlazione tra la posizione dei legami hanno effetti notevoli sia sulla termodinamica sia sulla dinamica del sistema: nel diagramma di fase, sono osservabili luoghi di minimi di compressibilità isobara, massimi di densità isobara, massimi di calore specifico isobaro e massimi di viscosità isoterma. Un'ipotesi recente, confermata da lavori di simulazione numerica ma non ancora sperimentalmente, suggerisce che queste anomalie, dovute alla presenza di una forte correlazione nella formazione dei legami, siano i primi segnali dell'esistenza di un nuovo punto critico liquido-liquido. Per temperature sufficientemente basse, si ritiene che i liquidi network forming possano separarsi in due distinti liquidi con diverso ordinamento nell'orientazione di molecole.

Dinamica

Rispetto allo stato gassoso, in cui la traiettoria delle particelle può essere modellizzata come una sequenza di traiettorie rettilinee interrotte dalle collisioni tra particelle e il cammino libero medio è significativamente più grande di σ, la densità maggiore che caratterizza i liquidi implica che le traiettorie atomiche siano sempre fortemente condizionate dalle collisioni, cosicché la presenza di disordine nelle posizioni si riflette anche nella dinamica. Nei liquidi si distingue comunemente tra dinamica collettiva e dinamica self: la prima descrive il moto delle fluttuazioni di densità, scomposta per il tramite dell'analisi di Fourier nelle sue componenti ϱ_k con differente vettore d'onda k; tale scomposizione consente di studiare in che modo una fluttuazione con lunghezza d'onda λ≈|k|⁻¹ si propaghi ed eventualmente si smorzi nel tempo, al variare di λ. La dinamica self descrive il moto di una tipica particella nel tempo. Nel limite idrodinamico, in cui le distanze sono molto maggiori delle dimensioni atomiche o molecolari, la dinamica delle fluttuazioni collettive di densità è calcolabile a partire dalle leggi di conservazione della densità, della quantità di moto e dell'energia, utilizzando equazioni costitutive che introducono la viscosità di taglio e di volume e la conducibilità termica. È possibile osservare, per esempio con esperimenti di diffusione di luce con lunghezza d'onda molto maggiore rispetto alle distanze interatomiche, fluttuazioni di densità che si propagano con velocità c_s, analoghe ai modi longitudinali acustici nei solidi, e fluttuazioni smorzate, la cui scala temporale è controllata dalla diffusività termica D_T. Nel limite idrodinamico, c_s è costante e le onde sonore longitudinali di lunghezza λ, che oscillano nella stessa direzione della propagazione, possono propagarsi con periodo T=λ/c_s, con valori tipici di c_s≈1000 m/s.

Al diminuire di λ, il regime idrodinamico, in cui il liquido può essere descritto come un continuo, è sostituito da quello microscopico, in cui il disordine della struttura interferisce con la dinamica. Quale sia la lunghezza d'onda che discrimina tra i due regimi è ancora oggetto di indagine. Quando le fluttuazioni di densità avvengono su distanze confrontabili con quelle interatomiche, l'osservazione sperimentale richiede l'uso di raggi X o neutroni. Per valori piccoli di λ sono presenti moti di propagazione sia longitudinali, sebbene molto attenuati rispetto agli analoghi modi idrodinamici, sia trasversali. La velocità di propagazione diviene dipendente da λ, fino ad annullarsi per distanze dell'ordine di quelle tra primi vicini. La possibilità che si propaghino onde trasversali, che trasmettono sforzi di taglio, è un'indicazione della natura quasi-solida del liquido su scala temporale microscopica. A differenza dei solidi ordinati, il disordine intrinseco nella struttura mescola le proprietà dei modi, facendo sì che le fluttuazioni acquisiscano caratteri sia trasversali sia longitudinali. Per distanze molto piccole rispetto alle distanze tra le particelle, infine, le fluttuazioni di densità riflettono la propagazione balistica delle particelle e si possono osservarei effetti quantistici.

L'analisi statistica dell'evoluzione temporale delle fluttuazioni di densità è basato sullo studio delle loro funzioni di autocorrelazione, che formalmente evolvono obbedendo a equazioni di Langevin generalizzate, con un termine di memoria non locale e non istantaneo. Dal punto di vista formale, lo studio attuale della dinamica collettiva dei liquidi è incentrato sulla modellizzazione di tale funzione di memoria.

La dinamica self descrive statisticamente il moto di una generica particella nel tempo. Dal punto di vista sperimentale, può essere indagata con tecniche di diffusione anelastica di neutroni, in particolar modo in campioni in cui è presente un forte segnale incoerente. La descrizione completa della dinamica self richiede il calcolo, oppure la misurazione, della probabilità che una particella che al tempo t=0 è nell'origine si trovi in r a un instante di tempo t generico. Di tale funzione sono noti due limiti, entrambi funzioni gaussiane di r: il limite di moto balistico per tempi molto brevi e quello di moto diffusivo per tempi molto lunghi. Nel primo caso P(r,t)≈exp(−βmr²/6t²), mentre per tempi lunghi P(r,t)≈exp(−r²/6Dt), dove con m è indicata la massa della particella e con D il coefficiente di diffusione. Il comportamento per tempi intermedi, compresi tra il regime balistico e quello diffusivo, è ancora di difficile modellizzazione. È importante notare come in un processo diffusivo, in cui il tempo cresce con il quadrato della distanza percorsa in media, la relazione tra tempo e spazio, r≈(t)^1/2, sia diversa rispetto al caso di propagazione balistica, in cui r≈t. Il processo diffusivo, nella sua versione più semplice, descrive il moto di una particella che a ogni intervallo temporale τ compie in una direzione a caso un percorso di lunghezza l. In queste condizioni, D è esprimibile come l²/6τ. Inserendo i valori tipici dei liquidi semplici per la distanza interatomica e per il tempo tra due urti, ossia l≈Å (1 Å=10⁻¹⁰ m) e τ≈ps (1 ps=10⁻¹² s), si ha D≈10⁻⁵ cm²/s, che predice il corretto ordine di grandezza del coefficiente di diffusione nella fase liquida intorno a T_t.

A differenza della statica, la dinamica dei liquidi, anche di quelli semplici, non è ancora totalmente compresa, in particolare nelle condizioni di sottoraffreddamento illustrate nel seguito.

Simulazioni numeriche

La fisica dei liquidi è uno dei campi in cui si è fatto largo uso di tecniche di simulazione numerica. Le difficoltà intrinseche nella descrizione teorica dello stato liquido, volta a predire le proprietà del sistema a partire dal potenziale v(r), hanno privilegiato lo sviluppo di tecniche numeriche che potessero fornire dati termodinamici, strutturali e di dinamica 'esatti' una volta noto il potenziale. Il lavoro numerico stabilisce un ponte tra teoria e sistemi reali, per i quali non sempre v(r) è noto. Le tecniche numeriche sono utilizzate per generare un insieme di configurazioni del liquido attraverso la generazione nello spazio delle configurazioni di una traiettoria, che può essere il risultato della dinamica newtoniana (nel cui caso si parla di dinamica molecolare) oppure di un processo stocastico capace di dare origine alla corretta distribuzione di equilibrio (Metropolis Monte Carlo); l'analisi delle configurazioni consente di calcolare le proprietà del sistema. Le risorse computazionali attuali, applicate a tali tecniche, permettono di studiare sistemi composti da 10⁵-10⁶ particelle, per intervalli temporali di decine di nanosecondi (1 ns=10⁻⁹ s).

Di più recente sviluppo, ma ancora limitate a sistemi composti da poche centinaia di atomi, sono le tecniche di simulazione ab initio, in cui la propagazione dei cosiddetti nuclei del sistema avviene nel potenziale determinato dagli elettroni, il cui stato fondamentale è aggiornato continuamente. Questa linea di ricerca, nel cui ambito il metodo più efficiente è stato sviluppato da Roberto Car e Michele Parrinello, non richiede la conoscenza a priori del potenziale di interazione tra le particelle. Nonostante il limitato numero di nuclei e la brevità del tempo fisico riprodotto nella simulazione, questa tecnica permette di studiare i sistemi nei quali gli effetti quantistici giocano un ruolo non trascurabile, quelli in cui avviene una significativa ridistribuzione delle cariche elettriche al variare della densità e della temperatura e i fenomeni di trasferimento di carica nei legami chimici.

Metastabilità

Lo stato liquido, come stato di equilibrio, cessa di esistere alla temperatura di solidificazione (o di fusione) T_m. Per temperature inferiori, lo stato cristallino ha un'energia libera minore rispetto a quella dello stato liquido ed è quindi stabilizzato termodinamicamente: il liquido prima o poi si trasforma in un solido attraverso una transizione del primo ordine, innescata da una fluttuazione termica capace di generare un nucleo cristallino di dimensioni critiche. Il tempo medio per la generazione del nucleo critico è infinito alla temperatura T_m e varia raffreddando il liquido; se i tempi caratteristici della dinamica collettiva del liquido sono inferiori rispetto ai tempi di enucleazione, il liquido esiste come stato metastabile e prende il nome di liquido sottoraffreddato. Se dal punto di vista strutturale i cambiamenti che il sottoraffreddamento introduce in S(q) e g(r) sono trascurabili, la dinamica molecolare cambia invece radicalmente. In un intervallo limitato di temperature, i tempi caratteristici del sistema variano dal picosecondo alle centinaia di secondi, coprendo un intervallo dinamico di oltre quattordici ordini di grandezza. Variazioni della medesima entità riguardano l'aumento della viscosità e la diminuzione del coefficente di diffusione, mentre le fluttuazioni trasverse si propagano su distanze che divengono macroscopiche. Nello stesso intervallo di temperature si osserva una diminuzione dell'entropia in eccesso, vale a dire della differenza di entropia tra il liquido e il cristallo, e ciò suggerisce una significativa diminuzione del numero di configurazioni accessibili al liquido. Vicino alla transizione vetrosa, definita operativamente come la temperatura o la pressione a cui la viscosità raggiunge 10¹¹ poise (1poise=10⁻¹ Pa s), un atomo impiega ≈1 s per diffondere attraverso una distanza pari a quella tipica tra due vicini, nonostante la sua velocità media non sia molto diversa da quella che aveva intorno a T_t, per cui bastava ≈ 1 ps. In queste condizioni, il liquido può essere visto come un sistema che è localizzato per tempi macroscopici in una regione ristretta dello spazio delle fasi e che cambia la sua configurazione soltanto mediante transizioni infrequenti, un'idea sviluppata nel formalismo del cosiddetto paesaggio di energia (libera o potenziale). Nel tempo compreso tra transizioni, il liquido si comporta a tutti gli effetti come un solido disordinato. In condizioni di sottorafreddamento, infatti, le fluttuazioni di densità decadono su due scale temporali ben separate: una veloce (≈ps), poco sensibile alla temperatura, che riflette processi vibrazionali microscopici intorno a una struttura fissata, e una lenta, che varia per diversi ordini di grandezza con la temperatura e che riflette il processo di ristrutturazione del liquido chiamato rilassamento strutturale, o α. Per tempi piccoli rispetto al tempo di rilassamento strutturale il sistema si comporta come un solido.

Tra i temi di ricerca più attuali si annoverano lo studio del rallentamento della dinamica che precede la transizione vetrosa, la descrizione di tale transizione nella sua forma ideale (non realizzabile in condizioni di equilibrio metastabile, perché i tempi necessari divergono), lo studio delle condizioni che regolano la propensione del sistema a formare un vetro piuttosto che un cristallo (ossia quali aspetti del potenziale fanno sì che il tempo di nucleazione sia sempre maggiore dei tempi di rilassamento, anche quando questi crescono di svariati ordini di grandezza) e infine lo studio della posizione relativa delle curve di transizione vetrosa e di separazione liquido-gas. È possibile portare il liquido in condizioni di metastabilità anche rispetto allo stato di gas, sia incrementandone la temperatura oltre quella di ebollizione, sia aumentandone progressivamente il volume in condizioni di sforzo tensile, grazie alla presenza di forze attrattive tra particelle. In entrambi i casi, la transizione alla stabilità richiede la formazione di un nucleo di gas all'interno del campione; per esempio, l'acqua degassata a pressione ambiente può essere sovrariscaldata di circa 100 gradi e sottoposta a pressioni negative di 100 MPa (1000 bar).

Il futuro vicino: 'nanoliquidi'

Tra gli attuali campi di frontiera nella fisica dei liquidi, un ruolo importante è riservato allo studio delle soluzioni colloidali e dei liquidi composti da macromolecole, per esempio polimeri e cristalli liquidi. Questi sistemi, classificati oggi come materia soffice, ampliano considerevolmente il campo di applicazioni della fisica dei liquidi. Qui ci si limita a evidenziare alcune novità introdotte nello studio delle soluzioni colloidali nel campo dei liquidi. Nei casi più semplici, una soluzione colloidale è costituita da particelle di dimensioni mesoscopiche (dalle decine di nm ai μm) dissolte in un solvente, la cui granulosità può essere considerata trascurabile; in molti casi, le particelle colloidali possono essere trattate come atomi giganti interagenti. A differenza dei sistemi atomici e molecolari, le interazioni tra particelle colloidali sono modulabili dall'esterno con perturbazioni delle proprietà del solvente, con l'introduzione di cosoluti o con la progettazione chimica delle proprietà delle superfici delle particelle medesime. Dal punto di vista sperimentale, l'uso di particelle di dimensioni confrontabili con la lunghezza d'onda della luce permette di utilizzare tecniche di microscopia ottica per lo studio dei campioni e di raggiungere una descrizione altamente dettagliata, sia statica sia dinamica. Diviene anche possibile, mediante tecniche di optical tweezing, muovere dall'esterno singole particelle e ampliare notevolmente sia la capacità di analizzare i sistemi sia quella di applicare su scala mesoscopica perturbazioni esterne.

La facoltà di disegnare il potenziale di interazione consente di andare oltre le possibilità di esplorazione proprie dei sistemi atomici e molecolari. Con i sistemi colloidali è stato infatti possibile realizzare il fluido di sfere dure, utilizzando una soluzione di palline di polimetilmetacrilato (PMMA) stabilizzate in un apposito solvente. Le misure riproducono con precisione le proprietà note del modello di sfere dure.

Si può inoltre modificare ad hoc il sistema, e aggiungere una componente attrattiva al potenziale, variando con continuità il raggio d'azione dell'interazione tra le particelle colloidali. Una possibile realizzazione fa uso dell'attrazione che si genera per fenomeni di svuotamento aggiungendo in soluzione ulteriori particelle colloidali (o polimeri) di dimensioni molto inferiori. Ciò ha mostrato che lo stato liquido richiede, come stato di equilibrio, non soltanto una componente attrattiva nel potenziale di interazione, ma anche che il raggio di interazione sia dell'ordine di almeno un decimo rispetto alle dimensioni delle particelle.

Altri fenomeni non presenti nel caso dei sistemi atomici riguardano i potenziali in cui l'attrazione a corto raggio è accompagnata da una repulsione, tipicamente di origine elettrostatica, a lungo raggio. In questo caso, la struttura del fluido può essere composta da aggregati colloidali in equilibrio (cluster phases). Oggi si iniziano a progettare e a realizzare sperimentalmente particelle colloidali con potenziali di interazione asimmetrici (per es. incorporando sferette magnetizzate all'interno delle particelle colloidali) o con un numero finito di siti attrattivi sulla superficie del colloide, riproducendo su scala più grande la fisica dei liquidi associati. Nei prossimi anni si potrà assistere, contemporaneamente all'evoluzione, già in atto, della fisica dei liquidi in fisica dei sistemi interagenti disordinati, allo sviluppo di sistemi che riprodurranno, su scala da dieci a mille volte maggiore, i liquidi atomici e molecolari, ricreando non solamente un mondo in scala, ma anche una ricchezza di fenomeni notevolmente maggiore di quella osservabile nello stato liquido.

Bibliografia

Barrat, Hansen 2003: Barrat, Jean-Louis - Hansen, Jean-Pierre, Basic concepts for simple and complex liquids, Cambridge, Cambridge University Press, 2003.

Binder, Kob 2005: Binder, Kurt - Kob, Walter, Glassy materials and disordered solids. An introduction to their statistical mechanics, Singapore, World Scientific, 2005.

Car, Parrinello 1985: Car, Roberto - Parrinello, Michele, Unified approach for molecular dynamics and density-functional theory, "Physics review letters", 55, 1985, pp. 2471-2474.

Egelstaff 1994: Egelstaff, Peter A., An introduction to the liquid state, Oxford, Oxford Science; Clarendon, 1994.

Hansen, McDonald 1986: Hansen, Jean-Pierre - McDonald, Ian R., Theory of simple liquids, 2. ed., London, Aca-demic Press, 1986.

Mzard, Parisi 1999: Mzard, Marc - Parisi, Giorgio, Thermodynamics of glasses: a first principles computation, "Physics review letters", 82, 1999, pp. 747-750.

Poole 1992: Poole, Peter H. e altri, Phase behavior of metastable water, "Nature", 360, 1992, pp. 324-328.

Sciortino, Tartaglia 2005: Sciortino, Francesco - Tartaglia, Piero, Glassy colloidal systems, "Advances in physics", 54, 2005, pp. 471-524