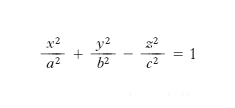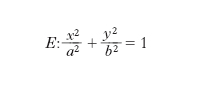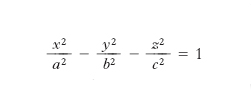iperboloide
Quadrica a centro (non specializzata, cioè diversa da un cono), dotata di infiniti punti reali, avente una conica impropria non degenere. Ammette generalmente, oltre a un centro di simmetria, tre assi e tre piani di simmetria. Assumendo questi ultimi come piani coordinati, la sua equazione canonica può risultare di due diverse forme in corrispondenza a due diversi tipi di i.: i. a una falda (o iperbolico o a punti iperbolici), di equazione canonica
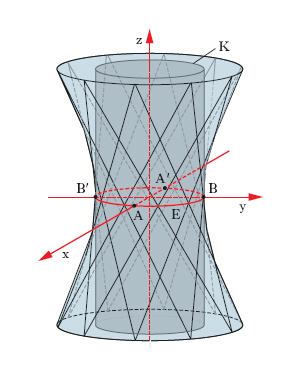
La superficie è connessa, si estende all’infinito, contiene due sistemi di rette reali (in fig. 1 ne è rappresentata la porzione racchiusa tra due piani paralleli), sta tutta al di fuori del cilindro retto K che ha per
base, sul piano xy, l’ellisse (v. formula)
E è detta ellisse di gola dell’i. perché è la più piccola ellisse che si possa tracciare sulla superficie.
L’i. e il cilindro K sono tangenti in ciascun punto di E. L’i. ha quattro vertici, A, A′, B′, B, che sono i suoi punti di intersezione con gli assi x e y.
Quando a=b, la superficie risulta rotonda e si può immaginare generata dalla rotazione di un’iperbole attorno al suo asse non trasverso (preso come asse delle z), oppure dalla rotazione attorno all’asse z di una retta sghemba con esso. I. a due falde (o ellittico o a punti ellittici), di equazione canonica
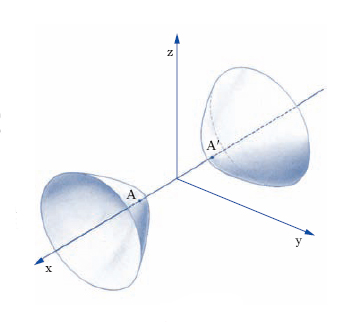
La superficie si compone di due falde a forma di ‘coppe’, rivolte in senso opposto ed estese all’infinito; in fig. 2 è illustrata la parte di superficie compresa tra due piani paralleli e simmetrici rispetto al piano yz. L’i. a due falde ammette due vertici, A, A′, suoi punti d’intersezione con l’asse x.
Quando b=c, la superficie è rotonda e si può immaginare generata da un’iperbole rotante intorno all’asse trasverso (Archimede chiamava ogni falda della superficie conoide ottusangolo).