involuzione
Biologia
In embriologia, movimento morfogenetico che determina lo spostamento di un’area della blastula la quale, scorrendo intorno al labbro del blastoporo, viene invaginata e portata nell’interno dell’embrione.
Processo graduale e continuo che determina l’atrofia di alcuni organi; questa è l’i. dovuta all’età, ma un’infezione può accelerare il processo normale. Esempi di i. normale sono: l’i. del timo dopo la pubertà; l’i. dell’apparato genitale dopo la menopausa; l’i. dell’utero dopo il parto; l’i. dei testicoli a tarda età.
Si dice età involutiva l’età presenile e senile, con riferimento al progressivo decadimento delle funzioni biologiche e delle capacità psichiche e sociali dell’individuo. In psichiatria si parla di depressione, di paranoia, di parafrenia involutiva a indicare i rispettivi quadri psicotici a inizio tardivo o le psicosi depressive che compaiono durante il periodo involutivo.
Matematica
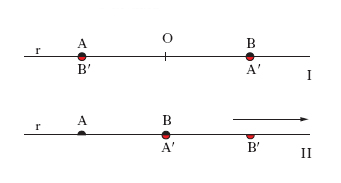
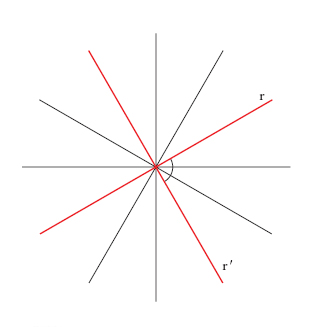
Nella geometria proiettiva, l’i. è una proiettività non identica tra forme di prima specie sovrapposte, nella quale ogni coppia di punti corrispondenti è involutoria, cioè: se all’elemento A corrisponde, nella proiettività data, l’elemento A′, ad A′, concepito però come un elemento B della prima forma, corrisponde, nella seconda forma, un elemento B′ coincidente con A. Per es., su una retta r (fig. 1, I) la simmetria rispetto a un punto O della retta stessa è una i.; non è tale, invece, una traslazione di data ampiezza (fig. 1, II), perché in essa B′ è diverso da A. È da osservare che se una proiettività ammette anche una sola coppia involutoria di elementi distinti, essa è un’involuzione. Un’i. può ammettere, dal punto di vista reale, due elementi uniti, cioè gli elementi che nella trasformazione corrispondono a sé stessi, o nessuno, e si chiama rispettivamente iperbolica o ellittica. Gli elementi uniti di una i. si chiamano anche doppi. Un esempio di i. iperbolica è quello, prima ricordato, della simmetria su una retta (fig. 1), in cui il punto O è doppio. I. assoluta nel piano euclideo È l’i., definita sulla retta impropria, nella quale le coppie di punti corrispondenti sono i punti impropri di coppie di rette ortogonali; i punti uniti, che sono complessi, sono detti punti ciclici. I. ortogonale o degli angoli retti (in un fascio di rette) È quella che a ogni retta r del fascio fa corrispondere la retta r′ a essa ortogonale (fig. 2); le rette doppie, il cui coefficiente angolare è un numero complesso, sono dette rette isotrope. L’i. ortogonale, intersecata con la retta impropria, dà luogo all’i. assoluta.