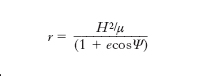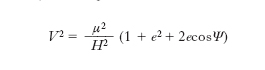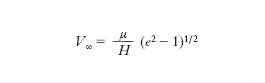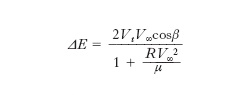fionda
Storia
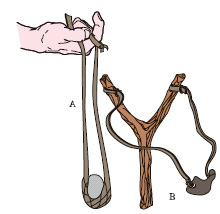
Arma da lancio o da getto ancora usata nel 16° sec. dai Francesi per lanciare granate a mano (per l’uso nel mondo antico ➔ fromboliere). Nella sua forma più comune era costituita da due bracci di corda (fig. 1A) con nel mezzo una rete o un pezzo di cuoio a forma di navicella o borsetta in cui si pone il proiettile; uno dei bracci ha un cappio all’estremità, tenuto dal dito indice; l’altro, più lungo del precedente, va stretto tra il pollice e l’indice; il lancio si compie facendo ruotare la f. sulla testa e lasciando poi il secondo dei due bracci, così che il proiettile sfugge a grande velocità.
Strumento usato per il lancio di piccoli proiettili, formato da due elastici (fig. 1B) fissati alle due estremità di un pezzo di legno o di ferro a forma di forca, e da un pezzo di cuoio che li unisce e su cui si appoggia il proiettile (di solito un sasso) da lanciare.
Astronautica
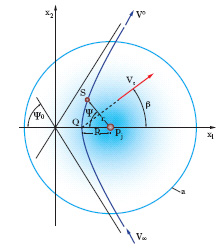
Effetto f. Tecnica proposta dal fisico G. Colombo per accelerare un veicolo spaziale, consistente nel dirigere la sonda verso un pianeta in modo che il moto di trascinamento di quest’ultimo ne aumenti l’energia cinetica (anche detto calcio planetario o flyby). Ogni pianeta ha una sua sfera d’influenza, definibile come la regione dello spazio in cui l’effetto del pianeta è predominante su quello di altri corpi celesti e il cui raggio varia a seconda della distanza del pianeta dal Sole. All’interno di tale sfera (fig. 2), il moto di un corpo attratto dal pianeta si può considerare non influenzato dagli altri corpi celesti; quando la sonda S è nella sfera d’influenza del generico pianeta Pj, la sua traiettoria relativa a Pj è, con ottima approssimazione, una iperbole, le cui caratteristiche sono determinabili per mezzo delle equazioni fondamentali della meccanica celeste e, in particolare, per mezzo del ‘problema dei due corpi ristretto’, che studia il moto di due corpi quando uno (in questo caso la sonda) è di massa trascurabile rispetto all’altro (il pianeta). Assumendo il pianeta come riferimento, la traiettoria della sonda rispetto al pianeta è una conica kepleriana, di cui il pianeta occupa uno dei due fuochi. L’equazione polare della conica è:
[1] formula
dove i simboli r e Ψ sono illustrati in fig. 2, e dove, nel caso iperbolico, si ha eccentricità e>1; con μ si è indicata la cosiddetta costante gravitazionale del pianeta (definita come il prodotto della massa del pianeta per la costante di gravitazione universale) e con H il momento della quantità di moto per unità di massa (prodotto della distanza della sonda S da Pj per la componente tangenziale della velocità relativa). Dall’equazione precedente si ottiene, per la velocità V:
[2] formula.
Queste relazioni sono valide per ogni tipo di conica: nel caso iperbolico, facendo tendere r all’infinito, si trova il valore limite cosΨ0 = –1/e dell’angolo Ψ che rappresenta l’inclinazione degli asintoti in fig. 2; sostituendo questo valore nella [2] si ottiene il valore della velocità all’infinito che prende il nome di velocità di eccesso iperbolico (VEI), la cui intensità V∞ è fornita da:
[3] formula.
È la VEI in intensità e direzione che definisce l’iperbole, insieme alla posizione del punto in cui la sonda entra nella sfera d’influenza del pianeta. Il pianeta è a sua volta in movimento con velocità Vt nota (quella di rivoluzione intorno al Sole) lungo la sua orbita, che in prima approssimazione, tenuto conto della brevità del passaggio, può essere considerata rettilinea. Si indica con β l’angolo che la direzione di Vt (cioè in sostanza l’orbita) forma con l’asse dell’iperbole. Per la valutazione della variazione di energia cinetica della sonda è necessario calcolare le due componenti della sua velocità, lungo l’asse dell’iperbole e normalmente a esso, all’ingresso della zona d’influenza e all’uscita. Il guadagno di energia cinetica per unità di massa della sonda è ottenuto come differenza dei quadrati delle velocità di uscita e di ingresso:
[4] formula
in cui R è la distanza minima del passaggio della sonda (PjQ in fig. 2). L’aumento (o la diminuzione) di energia cinetica ottenibile con la tecnica del flyby dipende dal pianeta sorvolato (tramite la costante μ), dalla velocità del pianeta Vt e dalle condizioni di sorvolo riassunte dalla VEI e dall’angolo β. L’effetto f. può essere usato per ritardare (cosβ〈0) o accelerare (cosβ>0) la sonda: quest’ultima applicazione è però l’unica attualmente utilizzata in quasi tutte le missioni interplanetarie perché consente un forte risparmio energetico.