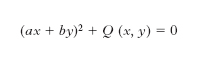cuspide
anatomia
Ciascun lembo delle valvole atrioventricolari del cuore.
Ciascun rilievo o tubercolo ben visibile sulla superficie triturante dei premolari e dei molari: nei primi ( bicuspidati), in numero di due; nei secondi ( multicuspidati), in numero di quattro.
Astronomia
Ciascuna delle punte con cui termina l’immagine della Luna o di un pianeta nei giorni immediatamente seguenti o precedenti la fase di congiunzione con il Sole. Per la Luna esse non presentano alcun effetto di crepuscolo che le allunghi, e questo prova l’assenza di un’atmosfera sensibile; in Venere, invece, la spessa atmosfera che circonda il pianeta ne produce un allungamento ( corna di Venere), che può talvolta chiudersi addirittura in un sottile anello luminoso.
Botanica
Estremità allungata e appuntita di un organo (foglia, boccio ecc.).
Matematica
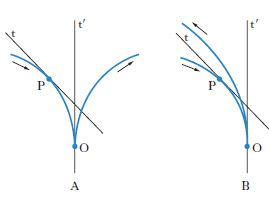
Si chiama c. (o punto di regresso; v. .) un tipo di punto singolare di una curva (il punto O). Intuitivamente, se si pensa la curva descritta da un punto mobile P, in una c. il punto P inverte bruscamente la direzione del suo movimento. Seguendo, durante il moto di P, le successive posizioni nella tangente t in P alla curva, possono presentarsi due casi: a) P inverte il senso del suo moto, mentre t non inverte il senso della sua rotazione attorno a O ( c. ordinaria o di prima specie; fig. A); b) anche t inverte il senso del suo moto ( c. a becco o di seconda specie; fig. B). La tangente t′ nella c. ( tangente cuspidale) lascia la curva, nel primo caso, parte da una banda e parte dall’altra; nel secondo, tutta da una stessa banda.
Dal punto di vista algebrico una c. è un punto doppio, nel quale vi è una sola tangente (due coincidenti) detta appunto tangente cuspidale, ed è origine di un ramo di secondo ordine della curva stessa (a differenza del nodo, che è un punto doppio con due tangenti distinte ed è origine di due rami lineari). La tangente ha tre intersezioni con la curva nel caso di una c. ordinaria, quattro nel caso della c. a becco. Esistono poi tipi più complessi di c. ( c. di specie superiore, come la c. di terza specie ecc.). Se una c. di una curva algebrica piana cade nell’origine, l’equazione della curva è del tipo:
dove ax + by = 0 (a e b non simultaneamente nulli) è l’equazione della tangente cuspidale e Q (x, y) è un polinomio che contiene soltanto termini di grado maggiore o uguale a tre.