quadratura
Astronomia
Due astri si dicono in q. quando la loro longitudine geocentrica differisce di 90°. Quando la Luna è in q. è al primo o all’ultimo quarto (e si dice marea delle q. la marea durante una di tali fasi lunari, con dislivelli minimi).
Fisica
Due grandezze armoniche, della stessa frequenza, si dicono in q. se la differenza tra le loro fasi vale ±(2k+1)π/2, con k nullo o intero (q. anticipo per il segno +, q. ritardo per il segno −).
Matematica
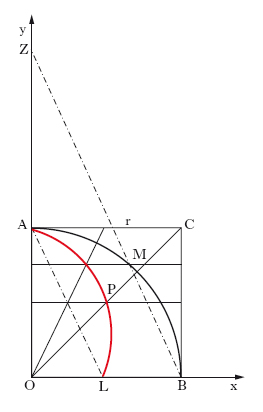
Nella geometria elementare, q. di una figura piana, problema consistente nella costruzione di un quadrato di area uguale a quella della figura data, sottintendendo il più delle volte che tale costruzione si possa eseguire con riga e compasso; in quest’ultima accezione, il problema può non ammettere soluzione, come per es. nel caso famoso della q. del cerchio (➔ cerchio), risolubile solo ricorrendo a mezzi di altro tipo, come la quadratrice, curva che permette di rettificare la circonferenza e, per conseguenza, di quadrare il cerchio. Esistono vari tipi di quadratrice, in particolare, quella di Ippia-Dinostrato: partendo da un quadrato OACB di lato r (v. fig.) e dal quadrante circolare AMB di centro O e raggio r, si faccia ruotare uniformemente la retta OA attorno a O, in senso orario fino a che si sovrapponga a OB; nello stesso intervallo di tempo la retta AC subisca una traslazione uniforme dalla posizione iniziale AC alla posizione finale OB (coincidente con la posizione finale di OA). Il punto P d’intersezione delle due rette mobili descrive allora una curva, appunto la quadratrice di Ippia-Dinostrato, la cui equazione cartesiana, riferita agli assi OB, OA, è y = x cotg(πx/2r). Il punto L in cui la quadratrice incontra l’asse x è tale che OL = 2r/π; quindi il segmento OZ tale che OL : r = r : OZ ha lunghezza πr/2, pari a un quarto di quella della circonferenza di raggio r.
Il termine quadratrice è anche usato nel calcolo integrale, come sinonimo di integrazione in quanto taluni integrali rappresentano aree di figure piane.