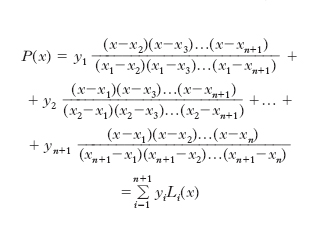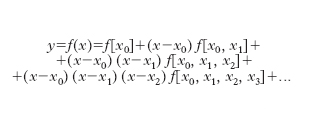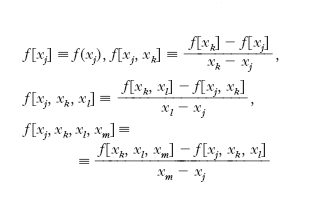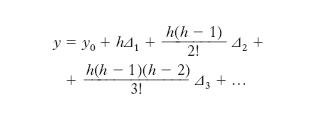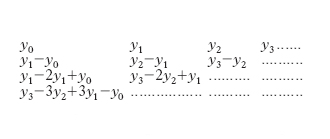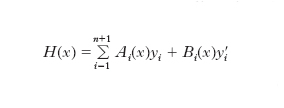interpolazione

Diritto

Nella scienza giuridica, ogni tipo di alterazioni, consistenti in aggiunte, omissioni e sostituzioni, subite dai testi giuridici da parte sia di commissioni legislative sia di commentatori e interpreti. Il problema delle i. riguarda tutte le fonti giuridiche antiche, soprattutto per la scienza del diritto romano, al punto che si può dire che quasi nessuna delle sue fonti ne sia rimasta immune. I. sono state segnalate sia nelle leges populi romani sia nelle fonti pervenute indipendentemente dalla compilazione giustinianea. Una gran massa di i. fu apportata dalle commissioni legislative giustinianee, presiedute da Triboniano (da cui il nome, alla i., di emblemata Triboniani), alle opere dell’antica giurisprudenza classica, da cui furono estratti i brani delle Pandette e delle Istituzioni, e al Codex di Giustiniano. La ricerca delle i. nella compilazione giustinianea fece i suoi primi passi col sorgere della scuola culta (16° sec.). Col decadere degli studi storici la ricerca delle i. decadde, per poi avere la definitiva ripresa con la fine del 19° sec., costituendo poi uno dei principali campi di indagini degli studi romanistici.

Matematica

fig. 1

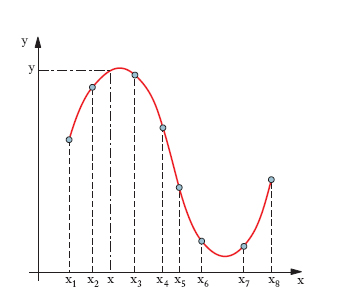
Procedimento con cui si calcola il valore di una grandezza y, dipendente da un’altra grandezza x, in corrispondenza di valori della x diversi da quelli per i quali sono a priori noti i valori della y stessa; in senso stretto, il termine indica il calcolo della y per valori della x compresi tra i valori anzidetti; per valori della x esterni all’intervallo determinato dai valori dati della x si parla piuttosto di estrapolazione. Il discorso può ripetersi per una grandezza y dipendente non da una sola, ma da più variabili. L’i. riesce utile allorché si vuole dare continuità a una serie di dati discontinui (i. logica dei dati) oppure sostituire a una serie di dati irregolari per errori accidentali o sistematici, una serie più regolare. Presupposto fondamentale della i., sia pure implicito, è che esista una certa regolarità nella dipendenza della y dalla variabile x. Quando si interpretino la y e la x come coordinate cartesiane (o di altro tipo) in un piano, il problema dell’i. si traduce geometricamente nel problema di tracciare una curva, quanto più regolare possibile, passante per i punti dati (o vicino a essi); essa si dice curva interpolatrice. Il problema dell’i., così come è stato enunciato, non ha soluzione unica; questa dipende evidentemente dal criterio adottato per calcolare i valori intermedi della funzione, cioè dal procedimento di i., che varia a seconda delle finalità che si vogliono raggiungere. A seconda del tipo di procedimento adottato si hanno, tra le altre, l’i. grafica, ottenibile tracciando a occhio, una curva che passi per i punti noti o tra i punti noti (fig. 1); l’i. per induzione, basata sull’andamento di casi analoghi a quello in esame, ovvero sulle relazioni che intercedono con altri fenomeni; e infine l’i. analitica, che si propone di determinare l’espressione analitica di una funzione, detta funzione interpolatrice, la quale o assume i valori noti della grandezza y, ovvero valori più o meno prossimi secondo opportuni criteri; in ogni caso occorre prefissare la forma analitica della funzione interpolatrice, che risulta, a priori, arbitraria.

fig. 2

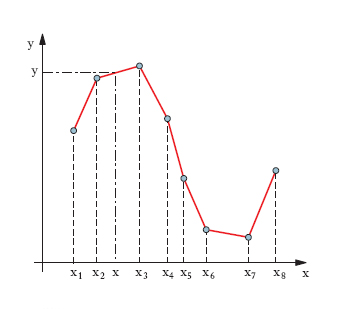
L’i. lineare è il tipo più semplice ed elementare di i.: quando della funzione siano noti i valori y1, y2 in due punti x1, x2, il procedimento consiste nell’assumere come grafico della funzione tra i due punti noti un tratto rettilineo, supponendo così che la funzione stessa sia lineare nell’intervallo x1 x2. In fig. 2 si è adottato il criterio dell’i. lineare nei singoli intervalli parziali x1x2, x2x3 ecc. L’i. lineare è correntemente usata per calcolare i valori delle funzioni tabulate (logaritmi, funzioni trigonometriche ecc.) per un valore della variabile che non figura all’ingresso della tavola, ma che è compreso tra due valori successivi dell’ingresso stesso.

La formula di i. di Lagrange fornisce un polinomio y=P(x), di grado non superiore a n, che assume, per i valori x1, ..., xn+1 della variabile x, certi n+1 valori prefissati y1, y2, ..., yn+1 e ha l’espressione

dove gli L_i(x) sono i cosiddetti coefficienti di Lagrange. Tale formula ha però lo svantaggio che, nel caso si aggiungano un nuovo valore x_n+2 della x e il corrispondente y_n+2 della y, è necessario calcolare daccapo tutti i termini di P(x). Sono perciò preferibili le formule seguenti. Noti che siano i valori y₀, y₁, y₂, ..., corrispondenti a x₀, x₁, x₂, ... (cioè y₀=f(x₀), y₁=f(x₁), y₂=f(x₂), ...), si ha:

formula d’i. di Newton, nella quale le quantità f[x₀, ..., x_n], differenze divise di ordine n, sono definite, in generale, nel modo seguente:

Nel caso frequente in cui le x_i siano i termini di una progressione aritmetica: xi=x₀+iδ, quella precedente si trasforma nella formula di Gregory-Newton, che si può scrivere:

in cui h=(x−x₀)/δ e Δ₁, Δ₂, ... sono le differenze successive dei numeri y₀, y₁, y₂, ... e compaiono nella prima colonna dello schema

nel quale gli elementi di ogni riga si ottengono, per differenza, dai due elementi più vicini della riga immediatamente superiore. Si noti che, quando il numero dei termini a secondo membro della formula è ridotto a due, la formula fornisce l’i. lineare tra i due valori y₀, y₁ assunti in x₀, x₁.

Nel caso in cui per i valori x₁, x₂ ... x_n+1 della variabile indipendente, si conoscono oltre ai valori delle y_i anche i valori delle derivate prime y′i, è possibile costruire un polinomio interpolatore della funzione y=f(x), di grado 2(n+1)+1, detto polinomio di Hermite. Questo polinomio può scriversi:

in cui Ai=[L_i(x)]²[1−2L′_i(x_i)(x−x_i)], e B_i=[L_i(x)]², essendo L_i(x) i coefficienti di Lagrange. Esistono inoltre formule, più complesse, relative al problema dell’interpolazione di una funzione incognita per mezzo di altri tipi di funzioni, per es., funzioni esponenziali.