commutatore
Fisica
Il c. [A, B] di due grandezze qualsiasi per le quali sia definito un prodotto AB è dato da [A, B]=AB−BA; semplici esempi di prodotti non commutativi, cioè che dipendono dall’ordine dei fattori e per i quali i c. non sono in generale nulli, sono il prodotto di due matrici oppure il prodotto vettoriale di due vettori (per il quale A×B=−B×A). In meccanica quantistica, a ogni quantità fisica osservabile (cioè misurabile) è associato un operatore lineare che agisce sullo spazio vettoriale degli stati del sistema; un operatore lineare si può rappresentare mediante una matrice finito- o infinito-dimensionale e di conseguenza il c. di due operatori lineari è in generale non nullo. Il c. di due osservabili ha un significato fisico centrale nella teoria della meccanica quantistica in connessione al principio di indeterminazione di W.K. Heisenberg. Infatti a due osservabili che non commutano non può essere simultaneamente assegnato un valore determinato. Ogni misura sul sistema che determini con una certa precisione il valore della prima osservabile perturba necessariamente il sistema in modo tale che risulta di conseguenza indeterminato il valore della seconda osservabile, tanto più quanto maggiore è la precisione della prima misura. Di conseguenza la determinazione esatta dei valori di un insieme completo di osservabili indipendenti che commutano rappresenta la conoscenza massima in linea di principio che si può avere dello stato del sistema che è quindi più limitata che in fisica classica.
Linguistica
Parola il cui referente può essere determinato solo nel contesto del messaggio, in quanto il suo senso varia a seconda della situazione comunicativa (come i termini qui, là, ora, ieri, questo, quello, io, tu).
Matematica
C. di due operatori lineari A e B è l’operatore AB-BA, che si indica spesso con il simbolo [A, B]. Se AB=BA si dice che i due operatori commutano tra loro, o sono tra loro permutabili.
Nella teoria dei gruppi, c. di due elementi a, b di un gruppo è l’elemento a–1 b–1a b: esso è l’elemento identico se e solo se a e b sono permutabili.
Tecnica
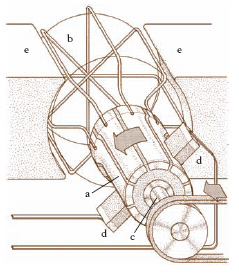
Organo delle macchine dinamoelettriche a corrente continua che serve a commutare le correnti variabili, che percorrono i circuiti dell’indotto, nella corrente unidirezionale che percorre il circuito esterno (v. fig.).
Dispositivo di manovra usato per cambiare sotto carico i collegamenti di due o più circuiti elettrici; l’operazione può essere manuale o automatica. Tra i più diffusi il c. a rotazione, il c. a leva (o c. a chiave) e il c. a scatti. Un c. è caratterizzato dal numero di vie (o di sezioni), cioè dal numero di correnti che possono fare capo a esso, e dal numero di posizioni, cioè dal numero di reofori su cui ognuna delle correnti può essere avviata. C. elettronico Dispositivo a multivibratori usato per avviare a uno stesso apparecchio vari segnali: per es., negli oscillografi a raggi catodici a più tracce, per commutare in sequenza i diversi segnali visualizzati. C. elettroottico Dispositivo che modifica il percorso di un segnale luminoso, mediante le variazioni che l’applicazione di un campo elettrico induce nelle proprietà ottiche del materiale di cui è composto (per es., niobato di litio).