catenaria

Enciclopedia on line

fig.

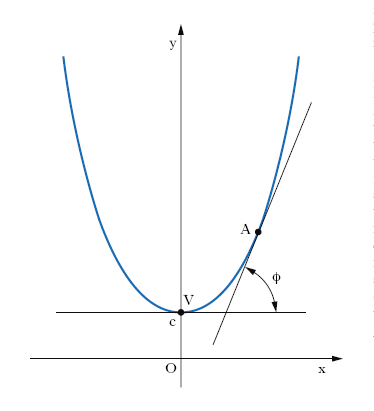
In geometria, curva piana trascendente caratterizzata dalla seguente proprietà differenziale: fissato un punto V della curva (v. fig.), la lunghezza di un arco, avente un estremo in V e l’altro estremo in un punto A variabile su di essa, è proporzionale alla tangente trigonometrica dell’angolo ϕ formato dalle due tangenti in V e in A alla curva stessa. La c. presenta un asse di simmetria e un vertice (il punto V). Assumendo l’asse y coincidente con l’asse di simmetria e l’asse x a distanza c dal vertice (v. fig.), l’equazione cartesiana della c. risulta:

formula

dove e è la base dei logaritmi naturali; l’asse x prende anche il nome di base o direttrice. La c. può anche ottenersi come luogo del fuoco di una parabola che rotola senza strisciare sopra una retta fissa. La c. ha speciale importanza in meccanica: un filo flessibile e inestendibile, omogeneo, soggetto al solo peso proprio, che sia sospeso in due punti (è il caso tipico di una fune o di una catena fissata ai due estremi) assume come configurazione di equilibrio un arco di catenaria. Come tale la c. fu presa in esame da Galileo, che però la identificò con una parabola (di cui ricorda la forma), e fu poi studiata da G.W. Leibniz, Giacomo Bernoulli e C. Huygens (che le diede il nome nel 1690).

Vedi anche
parabola neiloide In matematica, parabola di equazione y2=px3 (con p costante). tangente In geometria, si dice di ente (retta, linea, superficie ecc.) che abbia un particolare rapporto spaziale con altro ente della stessa natura, definito caso per caso e che riguarda comunque l’intersezione dei due enti considerati (che si dicono anche tra loro t.). In particolare, retta t. a una curva in ... figura simmètrica In geometria, si dice simmetrica (centralmente, assialmente o rispetto a un piano) una figura che corrisponde a sé stessa in una simmetria. Per es. il triangolo equilatero è una f.s. assialmente rispetto a tre assi, mentre il cerchio è una f.s. centralmente e rispetto ai suoi infiniti diametri. statica Parte della meccanica che studia l’equilibrio dei corpi sotto l’azione di determinate sollecitazioni; a seconda del sistema mediante il quale i corpi sono rappresentati si distinguono una s. del punto, una s. dei sistemi rigidi o stereostatica, una s. dei sistemi continui ecc. In particolare, nella scienza ...
Categorie
Tag
Altri risultati per catenaria
  • catenaria
    Enciclopedia della Matematica (2013)
    catenaria curva piana il cui andamento assume la configurazione di una fune (omogenea, perfettamente flessibile e non estensibile), soggetta soltanto al proprio peso e i cui due estremi siano vincolati a due punti fissi. La catenaria è una curva trascendente, la cui equazione si esprime mediante la ...
  • catenaria
    Dizionario delle Scienze Fisiche (1996)
    catenària [Der. di catena] [ALG] Curva piana non algebrica, caratterizzata dalla seguente proprietà differenziale: fissato (v. fig.) un punto V della curva, la lunghezza di un arco avente un estremo in V e l'altro estremo in un punto A variabile su di essa, è proporzionale, per una costante di proporzionalità ...
  • CATENARIA
    Enciclopedia Italiana (1931)
    La catenaria ordinaria è la curva piana secondo cui si dispone una fune o catena omogenea pesante, quando se ne fissino gli estremi: avendo essa l'aspetto generale di una parabola, Galileo aveva ritenuto fosse appunto una linea di tale specie; l'errore venne rilevato e corretto da C. Huygens. Nel piano ...
Vocabolario
catenària
catenaria catenària agg. e s. f. [der. di catena]. – 1. a. In geometria, curva piana non algebrica, luogo del fuoco di una parabola che rotola senza strisciare sopra una retta fissa. b. In meccanica, c. omogenea, configurazione di equilibrio...
catenòide
catenoide catenòide s. f. [comp. di catena e -oide]. – In geometria, superficie che si ottiene facendo ruotare una catenaria intorno alla sua direttrice.