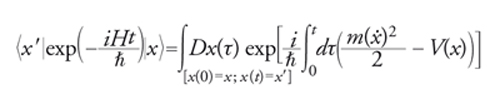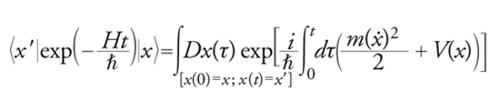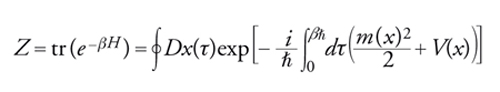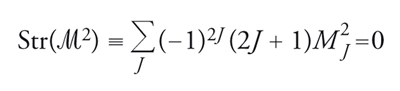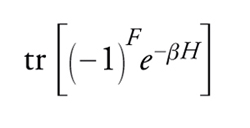Supersimmetria

Supersimmetria

Alla scala delle più piccole distanze esplorate attualmente, dell'ordine di 10⁻¹⁸ m, la materia appare costituita da combinazioni di poche decine di particelle le cui proprietà sono descritte dal Modello Standard. L'esigenza di comprenderne a fondo le implicazioni ha condotto a studi molto estesi della teoria quantistica dei campi, che del Modello Standard costituisce l'ossatura portante. Fondamentali in questo ambito sono i principî di simmetria, che portano alla distinzione tra simmetrie globali e simmetrie locali (o di gauge): le prime si riferiscono alle invarianze delle leggi fisiche sotto operazioni effettuate simultaneamente ‒ e in modo identico ‒ in tutti i punti dello spazio-tempo e sono all'origine delle leggi di conservazione; l'invarianza sotto traslazioni temporali, per esempio, dà luogo alla conservazione dell'energia, mentre simmetrie 'interne' non legate allo spazio-tempo sono all'origine della conservazione della carica elettrica e della stabilità della materia ordinaria. Le simmetrie locali corrispondono invece a trasformazioni indipendenti nei vari punti dello spazio-tempo e sono ritenute all'origine della struttura delle interazioni tra le particelle: un esempio particolarmente importante è la possibilità di modificare la fase della funzione d'onda in modo indipendente nei diversi punti dello spazio-tempo, che è ritenuta l'origine delle interazioni elettromagnetiche.

Le particelle elementari si suddividono in bosoni (per es., i fotoni), che hanno spin intero e tendono ad aggregarsi tra loro, e in fermioni (per es., gli elettroni), che hanno spin semintero e obbediscono al principio di esclusione di Pauli. Le masse dei fermioni e di alcuni bosoni di gauge traggono origine dalla rottura spontanea della simmetria, che richiederebbe l'esistenza del cosiddetto bosone di Higgs (una particella di spin nullo non ancora osservata sperimentalmente). Gli effetti delle fluttuazioni quantistiche tendono tuttavia a collocare la massa dei bosoni intermedi W ^± e Z alla scala di Planck, ben più elevata della scala elettrodebole, ponendo in tal modo il problema della gerarchia delle scale di massa.

Ove si tenti di armonizzare la descrizione della gravità offerta dalla relatività generale con la meccanica quantistica, si presentano difficoltà matematiche e concettuali, che alla scala di energia di Planck (dell'ordine di 10¹⁹ GeV) appaiono insormontabili. Al problema della gerarchia, si affianca inoltre quello della costante cosmologica: le attuali conoscenze a livello delle particelle elementari forniscono per la curvatura media dell'Universo una stima in totale disaccordo con il valore osservato. Ciò dipende dal fatto che i gradi di libertà bosonici e quelli fermionici non si bilanciano esattamente nel Modello Standard, che contiene almeno novanta gradi di libertà fermionici e soltanto ventotto gradi di libertà bosonici. La stima dell'energia di vuoto per unità di volume che ne risulta è in eccesso, rispetto ai dati sperimentali, per oltre cento ordini di grandezza.

Alcune teorie prevedono che bosoni e fermioni siano legati dalla cosiddetta supersimmetria, della quale esistono due tipi ben distinti di realizzazioni. In qualità di simmetria globale, essa scambia tra loro i campi associati alle particelle bosoniche e a quelle fermioniche, introducendo importanti restrizioni sulle loro proprietà e sulle loro interazioni. In qualità di simmetria locale, invece, la supersimmetria dà luogo a un nuovo tipo di interazione, mediata da un campo ‒ detto di gravitino ‒ che è allo stesso tempo un vettore (come il potenziale elettromagnetico) e un fermione (come i quark e i leptoni). I modelli corrispondenti si caratterizzano come estensioni della relatività generale e prendono il nome di supergravità.

Una supersimmetria globale esatta consentirebbe di risolvere tanto il problema della gerarchia quanto quello della costante cosmologica, ma a tutt'oggi una sua piena integrazione nella fisica delle particelle elementari incontra serie difficoltà: la più evidente è che la supersimmetria prevede l'esistenza di campi bosonici e fermionici a coppie e con uguali masse, differenziandosi profondamente dal Modello Standard, in cui le particelle sono in massima parte fermioni. Al pari della simmetria di gauge elettrodebole, che richiede la rottura spontanea e il fenomeno di Higgs, la supersimmetria non può quindi essere esatta, ma nella migliore delle ipotesi è interessata dal meccanismo della rottura spontanea, ponendo così una questione che si presenta come molto complessa. D'altra parte, le teorie supersimmetriche sono particolarmente attraenti dal punto di vista concettuale, in quanto unificano mediatori di interazione (γ, gluoni, W ^±, Z) e materia e presentano una struttura che consente costruzioni matematiche inapplicabili in altri contesti.

Modelli supersimmetrici

tab. 1

Una teoria di campo contiene contributi che, nell'intorno di una configurazione assegnata, sono esprimibili mediante uno sviluppo in potenze crescenti di campi bosonici e fermionici: i termini lineari definiscono gli accoppiamenti con sorgenti esterne, quelli quadratici caratterizzano i tipi e le proprietà delle particelle coinvolte, mentre i termini di ordine superiore definiscono la natura delle interazioni. La supersimmetria richiede che a ogni campo ne corrispondano altri nei quali esso possa trasformarsi e, pertanto, introduce restrizioni sia sulla natura dei campi sia sulle sorgenti, o sulle interazioni. Ci limiteremo a una breve descrizione delle collezioni di campi presenti in alcune teorie supersimmetriche, detti comunemente supermultipletti. Cerchiamo di chiarire la logica che determina la struttura dei termini quadratici. La tab. 1 mostra, a scopo esemplificativo, alcuni multipletti di campi di massa nulla presenti in teorie con una supersimmetria in quattro dimensioni (N=1; D=4). Il primo esempio, detto anche multipletto scalare o di Wess-Zumino, contiene uno scalare complesso φ (o, equivalentemente, due scalari reali) e un fermione di Weyl ψ (per inciso, se il numero D delle dimensioni è pari, un fermione di Dirac può essere scomposto in una coppia di fermioni di Weyl; nel caso D=4 un fermione di Weyl è equivalente a un fermione di Majorana, che descrive una particella di spin 1/2 priva di carica elettrica). Il caso successivo, del cosiddetto multipletto vettoriale, comprende un vettore A_μ e uno spinore di Weyl ψ. Il terzotipo di supermultipletto, detto multipletto della supergravità, contiene un vielbein, che descrive il campo gravitazionale, e un gravitino di Weyl, vale a dire uno spinore-vettore ψ_μ cui corrisponde una particella di spin 3/2 detta gravitino. La logica che sottende tutti questi casi è l'esatto bilanciamento del numero di gradi di libertà tra i bosoni e i fermioni: due per lo scalare complesso e due per il fermione di Weyl (con elicità ℏ/2 per la particella e −ℏ/2 per la corrispondente antiparticella) nel primo caso; due per il fermione di Weyl e due per il vettore (con elicità ±ℏ) nel secondo; due per il gravitone (con elicità ±2ℏ) e due per il gravitino (con elicità 3ℏ/2 per la particella e −3ℏ/2 per la corrispondente antiparticella) nel terzo. Il primo multipletto, a differenza degli altri, consente in modo naturale l'introduzione di masse uguali per lo scalare complesso e per il fermione; gli altri casi sono direttamente interessanti, in quanto le masse sono generate mediante una rottura spontanea che preserva la supersimmetria. Quest'ultimo meccanismo può essere discusso, a partire dal caso di massa nulla, in termini di multipletti che assorbono altri multipletti; per esempio, se un multipletto vettoriale ne assorbe uno scalare, si ottiene un multipletto vettoriale dotato di massa, che contiene un vettore massivo con tre polarizzazioni (che hanno origine dalle due del vettore originale di massa nulla e da quella di uno degli scalari del multipletto di Wess-Zumino), uno scalare reale e una coppia di spinori. In generale, è possibile mostrare che in quattro dimensioni i multipletti massivi contengono una catena di 2s+1 stati di spin s, due catene di 2s stati di spin s−1/2 e una catena di 2s−1 stati di spin s−1. Nel modello di Julius Wess e Bruno Zumino è possibile introdurre auto-interazioni del campo scalare φ, descritte per esempio da un potenziale, un polinomio in φ di grado superiore a due che la supersimmetria lega ad altre interazioni tra bosoni e fermioni. La struttura del multipletto vettoriale fissa completamente la forma della teoria N=1 SYM, nella quale la supersimmetria determina il tipo di interazione tra i campi di matrici A_μ e ψ.

Il multipletto di Wess e Zumino e il multipletto vettoriale sono alla base del Modello Standard supersimmetrico minimale (MSSM), la più semplice estensione supersimmetrica del Modello Standard che risulti compatibile con i dati sperimentali. La sua caratteristica essenziale è la sostituzione di ogni particella del Modello Standard con un super multipletto, ossia l'associazione di un partner supersimmetrico a ognuna delle particelle note: ai portatori di forze (gli otto gluoni, W^±, Z e γ) si aggiungono dodici fermioni (detti gaugini); ai quark e ai leptoni sono aggiunti altrettanti scalari complessi, detti s-quark e s-leptoni. Al fine di evitare che le fluttuazioni quantistiche diano luogo a risultati incoerenti (noti come anomalie), si rende inoltre necessario introdurre una coppia di multipletti di Higgs. La stabilità della materia ordinaria richiede che le possibili interazioni siano ristrette da una simmetria, detta R-parità, che implica che i processi di diffusione coinvolgano un numero pari di partner delle particelle note. Poiché una particella può decadere soltanto in altre di massa inferiore, il partner supersimmetrico più leggero (LSP) è stabile: la R-parità impone infatti che i prodotti di decadimento includano almeno un altro partner supersimmetrico, che ha massa necessariamente maggiore. Una simile particella fermionica priva di carica potrebbe costituire la cosiddetta materia oscura, che sembra essere all'origine di circa il 25% della densità di energia dell'Universo a fronte del 5% circa dovuto alla materia ordinaria. Il modello, tuttavia, in questa forma descriverebbe un mondo completamente supersimmetrico e pertanto esso va completato con opportuni meccanismi di rottura della supersimmetria, che in particolare provvedano a escludere partner troppo leggeri; a tutt'oggi non è stato possibile rilevare ciò in laboratorio. Il nuovo collisore LHC del CERN, che entrerà pienamente in attività entro il 2009, potrà fornire alcune risposte concrete sull'applicabilità di questo schema alla fisica delle alte energie e sui meccanismi di rottura di supersimmetria coinvolti. È opportuno rilevare che il numero dei parametri liberi aumenta considerevolmente rispetto a quelli del Modello Standard, ma di contro va riconosciuto al Modello Standard supersimmetrico minimale il merito di risolvere il problema della gerarchia e di rendere meno severo quello della costante cosmologica. La supersimmetria, infatti, anche in presenza di meccanismi di rottura garantisce la stabilità della scala elettrodebole rispetto alle fluttuazioni quantistiche. Il modello inoltre appare supersimmetrico a energie maggiori della scala M_sc² di rottura e, poiché tutti gli ulteriori contributi si cancellano esattamente, la stima proporzionale a M_Pl⁴ per la densità di energia del vuoto si riduce almeno a un valore proporzionale a M_s⁴. La scala M_sc² è peraltro limitata inferiormente dal valore di 1 TeV (circa mille volte l'energia di riposo di un protone) dai dati sperimentali attualmente disponibili (con la supersimmetria rotta genericamente a 1 TeV, la discrepanza tra stime microscopiche e macroscopiche relative alla costante cosmologica si ridurrebbe di almeno sessanta ordini di grandezza).

tab. 2

Una caratteristica del tutto peculiare del Modello Standard è che le interazioni deboli violano la parità, in quanto interessano in misura differente stati di spin collegati tra loro mediante riflessioni spaziali. È possibile mostrare che questa proprietà è compatibile al più con la supersimmetria N=1, ma è nondimeno interessante caratterizzare i modelli con più supersimmetrie. La tab. 2 riassume le caratteristiche salienti di alcuni multipletti di supersimmetria estesa, con N=2,4,8. La notazione ricorda che in questi casi esistono 2, 4 oppure 8 diversi tipi di trasformazioni che mescolano tra loro campi bosonici e fermionici. Anche se per ogni N tra 1 e 8 esistono teorie con campi di spin non superiore a due, abbiamo scelto di discutere questi casi perché caratterizzano le supersimmetrie estese compatibili con uno spin massimo dal valore rispettivamente 1/2 (N=2), 1 (N=4) e 2 (N=8). I modelli corrispondenti hanno un notevole interesse per i moderni sviluppi matematici della teoria dei campi.

I multipletti con spin massimo pari a 2 meritano una descrizione a parte, perché corrispondono a estensioni della relatività generale note come supergravità, in cui le interazioni gravitazionali e la simmetria che a esse sottende emergono dalla supersimmetria. In termini qualitativi, se un sistema possiede una coppia di simmetrie, in generale il risultato della loro azione combinata dipende dall'ordine con cui le trasformazioni sono applicate (per es., il risultato di due successive rotazioni intorno ad assi diversi dipende dall'ordine con cui esse sono operate). Ciò vale anche per una coppia di trasformazioni di supersimmetria, in cui due piccole trasformazioni operate in ordine opposto differiscono per un'altra piccola trasformazione. Questa ulteriore simmetria è sorprendentemente una traslazione spazio-temporale, un'operazione intimamente legata alla simmetria di gauge della relatività generale, e rende conto della profonda relazione tra la supersimmetria locale e la gravità. Esistono otto diversi tipi di supergravità pure, in cui è crescente il numero di gravitini che interagiscono tra loro, con il campo gravitazionale e con altri campi. Particolarmente complesse e ricche sono le interazioni che coinvolgono campi scalari, per le quali sono possibili eleganti rappresentazioni geometriche. I vari tipi di supergravità ammettono anche deformazioni in cui emergono, per i campi scalari, potenziali interessanti e i gravitini acquistano nuove interazioni con i vettori di gauge. Queste teorie sono state recentemente collegate in modo assolutamente sorprendente, nell'ambito della cosiddetta corrispondenza AdS/CFT, alla teoria N=4 SYM, che è basata sul quarto multipletto in tab. 2 e che contiene soltanto vettori, scalari e spinori.

tab. 3

È anche possibile generalizzare la costruzione dei multipletti al caso di uno spazio-tempo con più di quattro dimensioni e la loro struttura cambia in modo considerevole: in D>4 acquistano infatti un ruolo indipendente nuovi campi, mentre i gradi di libertà dei campi fermionici crescono in modo esponenziale con D. La tab. 3 riassume le proprietà dei multipletti in D=10,11. Nel primo caso esistono tre multipletti con al più campi di spin 2, detti rispettivamente di tipo I, IIA e IIB. Il rapido incremento delle componenti fermioniche ha un'importante conseguenza: una supersimmetria in D=10 corrisponde a quattro supersimmetrie in D=4 e pertanto il primo di questi casi è legato alle teorie con N=4, mentre gli altri due, che non si equivalgono in D=10, sono entrambi legati alla supergravità N=8 (per inciso, nei multipletti in D=10 gli spinori sono soggetti alle due proiezioni di Majorana e di Weyl, che in tal caso sono indipendenti e mutuamente compatibili, mentre lo spinore in D=11 è soggetto al vincolo di Majorana). In tutti questi casi il legame si manifesta attraverso il meccanismo di Kaluza-Klein: per esempio, se alcune dimensioni dello spazio-tempo in D=10 sono circonferenze molto piccole, per basse energie la teoria iniziale si riduce alle corrispondenti teorie in D=4. Il multipletto in D=11 è forse il più interessante: è unico e la corrispondente supergravità è particolarmente semplice, in quanto non contiene campi scalari. Queste teorie in D=10 e in D=11 coinvolgono interessanti generalizzazioni del campo elettromagnetico, i cui potenziali sono tensori antisimmetrici. L'esempio più semplice è il campo B_μν, presente in tutte le teorie in D=10: è possibile mostrare che, come le sorgenti del campo A_μ sono particelle cariche elettricamente, così quelle di B_μν sono stringhe; le sorgenti dei tensori antisimmetrici con un numero di indici maggiore sono in generale membrane, o in generale oggetti estesi con un numero maggiore di dimensioni. La comparsa di questo tipo di campi non è casuale: le teorie in D=10, infatti, sono intimamente legate alla teoria delle stringhe e in particolare alle stringhe supersimmetriche o superstringhe. Anche la supergravità in D=11 è legata alla teoria delle stringhe, ma in un modo più sottile, chiarito solamente in parte negli ultimi anni.

Risultati esatti nelle teorie supersimmetriche

Descriveremo ora in termini qualitativi alcune proprietà che rendono le teorie supersimmetriche uniche nel panorama della teoria quantistica dei campi. È conveniente richiamare anzitutto il concetto di integrale funzionale, sviluppato inizialmente da Richard P. Feynman. La meccanica quantistica fu formulata in origine nel linguaggio hamiltoniano, attraverso la sostituzione delle grandezze classiche con altrettanti operatori hermitiani; il principio di indeterminazione di Heisenberg trova infatti una naturale realizzazione in termini di operatori mutuamente non commutanti. Nonostante i successi iniziali in fisica atomica, emersero notevoli difficoltà, a causa di probabilità divergenti, nello studio delle interazioni elettromagnetiche. L'analisi richiedeva che venissero introdotte quante più semplificazioni possibili per ridurre la complessità dei calcoli e suggeriva il ricorso a metodi in grado di preservare a ogni stadio la simmetria di Lorentz. Dopo anni di ricerche, si giunse a concludere che le divergenze potevano essere rimosse mediante una procedura detta di rinormalizzazione, in grado di attribuire alle grandezze fisiche in esame valori ben definiti. Si devono a Feynman alcuni metodi di risoluzione originali basati sul formalismo lagrangiano e sulla raffigurazione intuitiva delle ampiezze di probabilità associate agli eventi di diffusione. Possiamo illustrarne gli aspetti essenziali considerando per semplicità il caso di una particella non relativistica, cui la meccanica classica associa una traiettoria x_c(t) ben definita, determinata dalle equazioni del moto: secondo il metodo indicato da Feynman, le ampiezze della meccanica quantistica possono essere ottenute attraverso un integrale funzionale, vale a dire mediante una somma pesata di numeri complessi associati a tutte le possibili traiettorie. Se ci riferiamo per esempio a una particella non relativistica di massa m e soggetta a un potenziale V(x), le ampiezze di evoluzione sono calcolate mediante la formula:

[4] formula

nella quale i denota l'unità immaginaria, H è l'hamiltoniano del sistema e l'espressione che compare a esponente è l'azione, ovvero l'integrale della lagrangiana. In generale, il calcolo esatto di questa espressione risulterebbe comunque oltremodo complesso ‒ non meno di quanto avviene nel formalismo hamiltoniano ‒ poiché richiederebbe una definizione precisa della misura di integrazione su tutte le possibili curve, uno spazio di dimensione infinita per il quale una caratterizzazione rigorosa è stata possibile soltanto in un numero limitato di casi. In molti esempi di interesse fisico è però possibile ordinare gli effetti della meccanica quantistica in una serie di potenze nelle costanti di accoppiamento o anche nella costante di Planck ℏ, secondo uno sviluppo che dal punto di vista tecnico non fornisce risultati esatti, ma ha essenzialmente la valenza di una serie asintotica. Come il metodo del punto di sella per le funzioni di variabile complessa, esso può comunque condurre a risultati molto accurati. In questo ambito, le correzioni quantistiche possono essere associate a contributi di traiettorie non troppo dissimili da x_c(t) o, in termini più squisitamente tecnici, a fluttuazioni intorno alla traiettoria classica. Il metodo fu accolto ben presto con grande favore, a dispetto del fatto che difettasse di rigore matematico, anche perché il calcolo approssimato delle ampiezze di diffusione tra le particelle è associato in modo assai ingegnoso a somme dei cosiddetti diagrammi di Feynman, che rappresentano a loro volta le traiettorie di particelle virtuali emesse e riassorbite nello spazio-tempo. È particolarmente adatto ai casi in cui le costanti di accoppiamento sono piccole e i diagrammi con pochi scambi di particelle determinano con buona approssimazione le probabilità di diffusione, ma si è rivelato inapplicabile in casi di accoppiamento forte. I diagrammi divergenti contengono anelli chiusi, nei quali le particelle possono circolare con impulso ed energia arbitrari; in generale, si ottengono valori finiti solamente introducendo un limite superiore Λ per le componenti dell'impulso. In un'ampia classe di teorie, dette appunto rinormalizzabili, la procedura di rinormalizzazione è in grado di eliminare i contributi che crescono con Λ e di condurre a risultati ben definiti, esprimibili in termini di un numero limitato di parametri desunti dagli esperimenti (masse e costanti di accoppiamento).

Il calcolo dell'integrale funzionale è stato esteso in seguito a fluttuazioni intorno a traiettorie più complesse. Le traiettorie più interessanti sono definite in realtà nello spazio euclideo, in cui l'integrale diventa:

[5] formula.

Questo importante filone di ricerca fu stimolato dalla cruciale scoperta, nel 1975 da parte di Alexander A. Belavin, Alexander M. Polyakov, Albert S. Schwartz e Yu.S. Tyupkin, di soluzioni definite nello spazio euclideo che rappresentano i fenomeni di tunnelling nel caso di sistemi con infiniti gradi di libertà. Tali soluzioni ‒ dette istantoni, perché concentrate intorno a un punto dello spazio-tempo euclideo ‒ rendono possibile il calcolo di effetti non perturbativi, O(e^−1/ℏ), non rappresentabili in serie di potenze di ℏ e altrimenti non accessibili. L'integrale funzionale appare oggi come il principale strumento di analisi non soltanto per la teoria dei campi, ma anche per la meccanica statistica. Per avere un'idea di questa connessione, si noti che ponendo x=x′ nella [5] e integrando sul loro valore comune si ottiene un'espressione che definisce la funzione di partizione:

[6] formula

dove β=1/k_BT, con k_B la costante di Boltzmann e T la temperatura assoluta. In questo caso l'integrazione è su traiettorie chiuse, per le quali x è periodica con periodo βℏ: x(βℏ)=x(0); per i campi fermionici la condizione di periodicità va sostituita con ψ(βℏ)=−ψ(0), a causa della peculiare relazione tra spin e statistica necessaria per avere coerenza con il principio di Pauli. Ma tale progresso concettuale non seguì, almeno inizialmente, un analogo progresso tecnico, tanto che i primi tentativi di introdurre nel Modello Standard gli istantoni per lo studio dei fenomeni non perturbativi, non esprimibili in termini di potenze di ℏ, furono piuttosto deludenti, in conseguenza della comparsa di divergenze ultraviolette.

Questo panorama cambia in modo considerevole per le teorie supersimmetriche, in cui a ogni bosone corrisponde un fermione, con effetti importanti a livello sia perturbativo sia non perturbativo: bosoni e fermioni contribuiscono con segni opposti a ogni anello chiuso nei diagrammi di Feynman, cosicché i loro contributi tendono a ridurre, o eventualmente a eliminare del tutto, le divergenze ultraviolette. La teoria N=4 SYM è un esempio particolarmente significativo: in questo caso è possibile mostrare che le divergenze ultraviolette sono del tutto assenti nelle ampiezze di diffusione. Questo tipo di cancellazioni fa il paio con un altro effetto, più semplice: le energie di vuoto di bosoni e fermioni hanno segni opposti e tendono parimenti a elidersi. In generale, la conclusione è che le teorie supersimmetriche coinvolgono divergenze più lievi rispetto ad altre teorie di campo e che, quindi, sono in un certo senso meno sensibili alle correzioni di tipo quantistico. Questo comportamento trova un'utile applicazione nel problema della gerarchia delle scale di massa, al quale abbiamo già accennato: masse bosoniche e fermioniche sono collegate tra loro e, pertanto, la relativa stabilità di queste ultime si trasmette per supersimmetria alle prime, stabilizzando in particolare i valori delle masse dei bosoni W ^± e Z.

Le interazioni che intervengono nella supergravità non consentono di portare avanti la procedura di rinormalizzazione, ma queste teorie godono nondimeno di proprietà notevoli. Per esempio, la proprietà della relatività generale di non dare luogo a divergenze ultraviolette nelle ampiezze di diffusione con un solo anello chiuso è condivisa dalle supergravità pure, nelle quali compare il solo multipletto di supergravità e non multipletti di materia. Per tali teorie, inoltre, la supersimmetria esclude la presenza di divergenze anche nelle ampiezze di diffusione con due anelli chiusi, e da anni si dibatte sull'ordine al quale queste divergenze potrebbero comparire nella supergravità N=8 (oggi si propende per il caso di diagrammi con almeno sette anelli chiusi, ma ulteriori sorprese sono possibili).

Anche nel regime non-perturbativo è possibile ottenere alcuni risultati esatti, grazie al fatto che le fluttuazioni dei campi bosonici e di quelli fermionici intorno a una soluzione istantonica supersimmetrica si compensano esattamente. In alcuni casi, l'integrale funzionale è determinato dalle sole proprietà di queste soluzioni e può essere calcolato sommando i contributi delle fluttuazioni quantistiche attorno alla soluzione istantonica. Questo calcolo è assai complesso in quanto la soluzione istantonica dipende da un certo numero di parametri continui la cui caratterizzazione matematica è molto difficile in generale, ma fortunatamente l'integrale funzionale può essere ricondotto a integrazioni finito-dimensionali sugli spazi di questi parametri. L'esatta definizione della misura corrispondente è stata il risultato di una proficua sinergia tra fisica e matematica.

Queste tecniche hanno inoltre reso possibile il calcolo delle correzioni quantistiche in una teoria supersimmetrica N=2 che richiama, sotto certi aspetti, la descrizione delle interazioni forti o di colore nel Modello Standard. Nel 1994, Nathan Seiberg ed Edward Witten sono infatti riusciti a mostrare che in questo modello le cariche portate dai campi fermionici sono esattamente confinate in composti neutri. Cerchiamo di spiegare brevemente la natura di questo problema. Negli anni Sessanta Murray Gell-Mann e George Zweig proposero che gli adroni, le particelle soggette alle interazioni forti, fossero composti da quark, più o meno come un nucleo è composto da protoni e neutroni. Si pose però il problema di spiegare perché i quark non si osservino in natura come liberi, ma si presentino soltanto in composti neutri rispetto alla carica di colore. Gerard 't Hooft, Stanley Mandelstam, Giorgio Parisi e altri notarono che la contemporanea presenza nel vuoto di cariche e monopòli potrebbe dar luogo al confinamento delle cariche di colore, rendendo impossibile la loro separazione in composti neutri. Tale meccanismo ricorda l'effetto Meissner, in grado di espellere campi magnetici dall'interno di un superconduttore: negli anni Trenta, Walter Meissner e Robert Ochselnfeld avevano infatti mostrato che campi magnetici deboli non penetrano all'interno di un superconduttore ideale (che oggi diremmo di tipo I). In realtà, in una vasta classe di superconduttori (che oggi diremmo di tipo II) campi magnetici di sufficiente intensità riescono a penetrare, ma solamente all'interno di piccoli tubi di flusso, nei quali sono compresse le linee di forza. L'energia in questi tubi cresce proporzionalmente alla loro stessa lunghezza e ciò crea una barriera che impedisce la separazione delle cariche magnetiche alle loro estremità. Nel caso delle interazioni forti di colore il meccanismo rilevante è legato al precedente da una dualità elettromagnetica: questa scambia campi elettrici e magnetici e le cariche corrispondenti, in modo tale che i piccoli 'tubi' terminano invece su cariche di colore, la cui separazione richiede parimenti un'energia che cresce linearmente con la distanza. Per dimostrare la plausibilità di questo scenario, è necessario mostrare che il vuoto della teoria contiene monopòli in grado di unirsi in coppie per dare origine alla superconduttività e quindi all'effetto Meissner duale, con il conseguente confinamento delle cariche di colore. Ebbene, questi risultati emergono in modo diretto dal calcolo esatto di Seiberg e Witten nella teoria supersimmetrica N=2, che rappresenta una delle più interessanti applicazioni della supersimmetria alla teoria delle interazioni forti.

Il problema della rottura della supersimmetria

La supersimmetria ha profonde implicazioni nella teoria dei campi. Per esempio, oltre a dare luogo alla cancellazione di divergenze, essa garantisce in generale ai sistemi a cui si applica una notevole stabilità. Il suo ruolo acquista quindi una rilevanza particolare nella teoria delle stringhe, la cui dinamica è oggi in massima parte fuori dalla nostra portata in assenza di supersimmetria. D'altra parte, le particelle elementari del Modello Standard non si presentano in multipletti supersimmetrici e una sua estensione supersimmetrica, per esempio il Modello Standard supersimmetrico minimale, deve quindi coinvolgere meccanismi di rottura, in grado di conferire masse sufficientemente elevate ai partner supersimmetrici delle particelle note, nessuno dei quali è stato a tutt'oggi rilevato. Ma i più semplici tra questi meccanismi si scontrano con una notevole regola di somma, scoperta nel 1979 da Sergio Ferrara, Luciano Girardello e Fabrizio Palumbo: nelle teorie supersimmetriche le masse dei campi bosonici e fermionici, in presenza di sole interazioni rinormalizzabili e quindi in assenza di gravità, e a meno di correzioni quantistiche, sono soggette al vincolo

[7] formula

dove J denota lo spin delle particelle, anche in presenza di rottura spontanea. Per un multipletto di Wess e Zumino, per esempio, questa relazione non consente di rendere i due bosoni più massivi del fermione: avremmo dovuto avere già osservato un partner scalare dell'elettrone; un'analisi accurata mostra l'impossibilità di giungere a un'estensione supersimmetrica soddisfacente del Modello Standard. Questa evidente difficoltà complica lo scenario per le teorie supersimmetriche; tuttavia esiste un'interessante via d'uscita, che ha il pregio di evidenziare un possibile, profondo legame tra il Modello Standard supersimmetrico minimale e la supergravità. In presenza di supergravità, infatti, a secondo membro della [7] compaiono termini che dipendono dalla massa del gravitino: in linea di principio, la rottura spontanea è quindi compatibile con i dati oggi disponibili, ma soltanto se la supersimmetria ha una piena realizzazione come simmetria locale.

Non esistono modi evidenti per determinare la scala della rottura della supersimmetria e, quindi, per predire la differenza di massa tra le particelle note e i loro eventuali partner. Non è quindi semplice escludere che questi scenari siano realizzati per energie ben oltre la nostra portata, ma se la scala di rottura della supersimmetria fosse dell'ordine di 1 TeV gli esperimenti in programma al collisore LHC potrebbero portare a una vera rivoluzione nella fisica delle particelle, contribuendo in parte anche a chiarirne i legami con la fisica della gravitazione. Se comunque la rottura della supersimmetria coinvolge in modo naturale la gravità, e quindi la natura dello spazio-tempo, scenari assai complessi, e solo parzialmente esplorati, sono possibili. Per esempio, come peraltro suggerito dalla teoria delle stringhe, la rottura della supersimmetria potrebbe essere indotta dalla presenza di oggetti estesi nel vuoto, oppure, in termini più squisitamente pittorici, da altri universi che comunicano con il nostro, mediante effetti radiativi.

Un risultato particolarmente elegante dovuto a Witten, in grado di indicare a priori se, per un dato sistema, la supersimmetria globale può essere rotta in conseguenza di effetti dinamici, può essere ottenuto partendo da un'equazione analoga alla [6], in cui anche i fermioni obbediscono a condizioni periodiche e che definisce una quantità nota appunto come indice di Witten:

[8] formula,

dove (−1)^F ha segni opposti per bosoni e fermioni. Tale indice in realtà non dipende da β: la supersimmetria, infatti, stabilisce una corrispondenza biunivoca tra eccitazioni bosoniche e fermioniche di un dato sistema, ma limitatamente a stati che corrispondono a energie non nulle dell'hamiltoniano. L'indice di Witten riceve pertanto contributi dai soli stati di energia nulla. Se in questi particolari stati è presente un eccesso di bosoni o di fermioni, l'indice è necessariamente non nullo e la supersimmetria è esatta, perché se gli stati in eccesso aumentassero la propria energia verrebbero a mancare i partner necessari. Tale indice definisce anche una notevole classe di integrali funzionali calcolabili esattamente e ha trovato una serie di importanti applicazioni nella teoria dei campi.

Conclusioni

Abbiamo esposto le ragioni del vasto interesse che, nonostante il persistere di alcune difficoltà, la supersimmetria riscuote nella comunità scientifica. Nella teoria dei campi (e in quella delle stringhe) essa consente di ottenere risultati esatti di grande eleganza, che forniscono indicazioni preziose sul comportamento di ampie classi di sistemi e che hanno stimolato sviluppi notevoli anche in matematica. Nelle estensioni del Modello Standard, la supersimmetria collega il bosone di Higgs a campi fermionici, migliorando in modo sensibile la stabilità della teoria elettrodebole rispetto agli effetti dovuti alle fluttuazioni quantistiche. In questo contesto essa fornisce alcuni candidati naturali per la materia oscura, che sembra dominare la composizione del nostro Universo. La supersimmetria è infine di aiuto, almeno in parte, per risolvere il problema della costante cosmologica. Il vero nodo della questione appare legato a una migliore comprensione dei meccanismi di rottura della supersimmetria, anche in vista dei dati che gli esperimenti potranno fornire nei prossimi anni.

Le origini della supersimmetria sono comunemente associate ai tentativi effettuati negli anni Sessanta di combinare le simmetrie interne con quelle spazio-temporali alla base della relatività speciale. Questa prospettiva si rivelò presto impraticabile nella sua forma originale, ma all'inizio degli anni Settanta i tentativi furono riconsiderati, inizialmente in Unione Sovietica, da Yuri A. Gol'fand, Evgeny P. Likhtman, Dmitrij V. Volkov e Vladimir P. Akulov, ed estesi a simmetrie in grado di scambiare bosoni e fermioni. Questi sviluppi, e altri a essi collegati, trassero anche importanti stimoli dalla teoria delle stringhe. Il vero culmine degli sforzi fu la costruzione, da parte di Wess e Zumino nel 1973, di un semplice modello in quattro dimensioni in cui la supersimmetria collega fermioni di spin 1/2 e bosoni di spin 0, un risultato che a differenza dei precedenti, suscitò un grande interesse nella comunità scientifica. Nel 1976 fu elaborato il primo esempio di supergravità, da parte di Daniel Freedman, Peter van Nieuwenhuizen e Ferrara; Ferdinando Gliozzi, Joël Scherk e David Olive riuscirono inoltre a collegare la supergravità alla teoria delle stringhe, dando origine alle superstringhe, che oggi sono un importante schema concettuale per l'unificazione della gravità con le altre interazioni fondamentali. Infine, nel 1978, Eugène Cremmer, Bernard Julia e Scherk, formularono la supergravità in undici dimensioni. In breve si giunse all'elaborazione del Modello Standard supersimmetrico minimale e, soprattutto, al chiarimento del suo possibile legame con la supergravità, grazie in particolare al contributo di Riccardo Barbieri, Ferrara e Carlos Savoy. Negli anni successivi sviluppi molteplici, di crescente sofisticazione matematica sono stati ispirati alla supersimmetria e al suo ruolo nella teoria delle stringhe. Queste ricerche sono state stimolate in modo sostanziale dai contributi di Witten, che hanno avuto un notevole impatto anche in matematica. Le ricerche condotte in quegli stessi anni hanno portato allo sviluppo delle superstringhe e hanno permesso di comprendere, per quanto in modo parziale, la natura unitaria dei principî che a esse sottendono, i loro legami con la supergravità e il ruolo di quest'ultima in relazione alla loro consistenza matematica; a tale proposito, va ricordata in modo particolare la scoperta da parte di Michael B. Green e John H. Schwarz del meccanismo di cancellazione delle anomalie che porta il loro nome. Tuttavia, il successo di molti tentativi di applicare queste idee alla fisica delle particelle elementari, resta a tutt'oggi parziale.

Bibliografia

Amati 1988: Amati, Daniele e altri, Non-perturbative aspects in supersymmetric Gauge theories, "Physics reports", 162, 1988, pp. 169-248.

Affleck 1984: Affleck, Ian - Dine, Michael - Seiberg, Nathan, Dynamical supersymmetry breaking in supersymmetric QCD, "Nuclear physics B", 241, 1984, pp. 493-534.

Affleck 1985: Affleck, Ian - Dine, Michael - Seiberg, Nathan, Dynamical supersymmetry breaking in four-dimensions and its phenomenological implications, "Nuclear physics B", 256, 1985, pp. 557-599.

Barbieri, Ferrara 1983: Barbieri, Riccardo - Ferrara, Sergio, Supersymmetry and fundamental interactions in the region of the Fermi scale, "Surveys in high energy physics", 4, 1983, pp. 33-67.

Bern 2000: Bern, Zvi e altri, Perturbative relations between gravity and gauge theory, "Classical quantum gravity", 17, 2000, pp. 979-988 (arXiv:hep-th/9911194).

Duff 1986: Duff, Michael J. - Nilsson, Bengt E.W. - Pope, Christopher N., Kaluza-Klein supergravity, "Physics reports", 130, 1986, pp. 1-142.

Duff 1995: Duff, Michael J. - Khuri, Ramzi R. - Lu, J.X., String solitons, "Physics report", 259, 1995, pp. 213-326.

Fayet, Ferrara 1977: Fayet, Pierre - Ferrara, Sergio, Supersymmetry, "Physics reports", 32, 1977, pp. 249-334.

Giudice, Rattazzi 1999: Giudice, Gian F. - Rattazzi, Riccardo, Theories with gauge-mediated supersymmetry breaking, "Physics reports", 322, 1999, pp. 419-499 (arXiv:hep-ph/9801271).

Green 1988: Green, Michael B. - Schwarz, John H. - Witten, Edward, Superstring theory, Cambridge, Cambridge University Press, 1988, 2 v.

Intriligator, Seiberg 1996: Intriligator, Kenneth A. - Seiberg, Nathan, Lectures on supersymmetric gauge theories and electric-magnetic duality, "Nuclear physics B: proceedings supplements", 39, 1996, pp. 1-28 (arXiv:hep-th/9509066).

Nilles 1984: Nilles, Hans Peter, Supersymmetry, supergravity and particle physics, "Physics reports", 110, 1984, pp. 1-162.

Polchinski 1998: Polchinski, Joseph, String theory, Cambridge, Cambridge University Press, 1998, 2 v.

Van Nieuwenhuizen 1981: van Nieuwenhuizen, Peter, Supergravity, "Physics reports", 68, 1981, pp. 189-198.

Weinberg 2000: Weinberg, Steven, The quantum theory of fields, Cambridge, Cambridge University Press, 2000, 3 v.

Wess, Bagger 1992: Wess, Julius - Bagger, Jonathan, Supersymmetry and supergravity, 2. ed., Princeton, Princeton University Press, 1992.

West 1990: West, Peter C., Introduction to supersymmetry and supergravity, Singapore, World Scientific, 1990.

Zwiebach 2004: Zwiebach, Barton, A first course in string theory, Cambridge, Cambridge University Press, 2004.