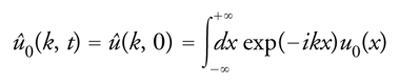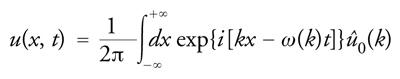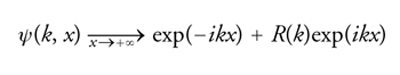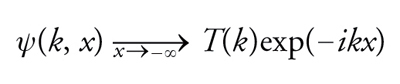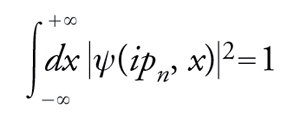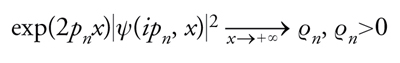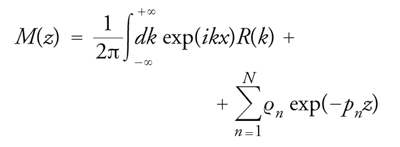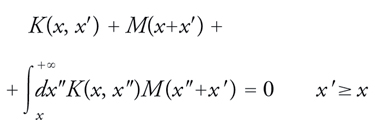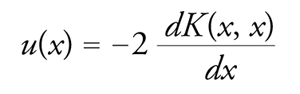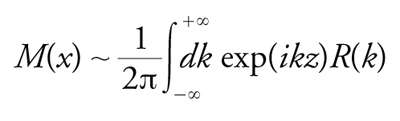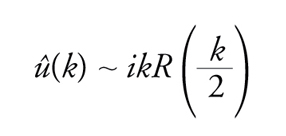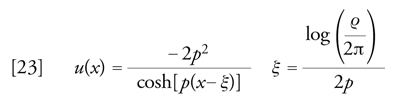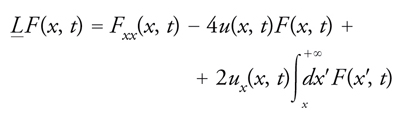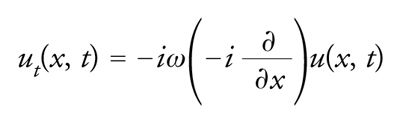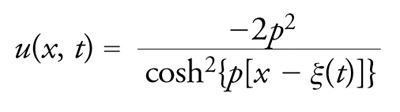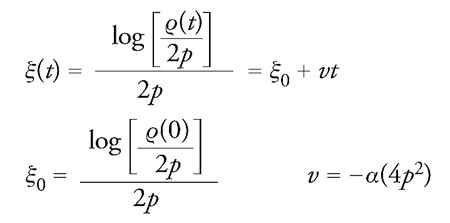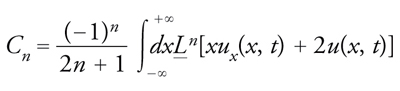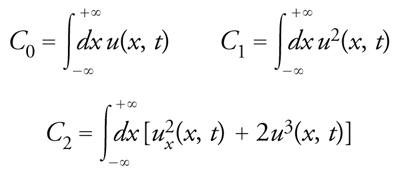Solitoni
Solitoni
La prima osservazione scientifica di un solitone, compiuta dall'ingegnere britannico John S. Russell durante l'osservazione di una massa d'acqua messa in agitazione in un canale dal moto di una barca, risale al 1834. Un importante progresso per la comprensione di questi fenomeni è stato compiuto alla fine del XIX sec., quando, per descrivere l'evoluzione temporale del profilo di un fluido in un canale poco profondo, fu introdotta un'equazione differenziale alle derivate parziali non lineare ‒ l'equazione di Korteweg-de Vries, in forma abbreviata KdV ‒ che nella sua versione matematica più semplice si presenta come (qui e nel seguito, le variabili a pedice indicano derivate parziali)
ut(x, t) + uxxx(x, t) − 6ux(x, t)u(x, t) = 0.
L'equazione KdV costituisce lo strumento più efficace per descrivere le proprietà matematiche dei solitoni e la connessa fenomenologia. Per il momento, basti osservare che esiste una particolare soluzione che rappresenta proprio una singola onda "di forma arrotondata, liscia e ben definita" che trasla "senza visibile cambiamento di forma o diminuzione di velocità":
formula
dove ξ(t)=ξ0+vt e v=4p2 (in questo caso la traslazione avviene verso destra, con una velocità tanto maggiore quanto più alto e stretto è il profilo della soluzione; il fatto che quest'ultima sia negativa è convenzionale e irrilevante, come anche la presenza del fattore −6 nella [1]). Questa proprietà e il fatto stesso che l'equazione KdV descriva efficacemente alcuni fenomeni naturali sono stati largamente ignorati nella prima metà del XX sec., presumibilmente a causa della mancanza di strumenti matematici idonei allo studio sistematico delle equazioni di evoluzione non lineari alle derivate parziali; in particolare a difettare è stata una metodologia matematica che, superando l'eventuale determinazione di teoremi sull'esistenza e unicità delle soluzioni, permettesse di comprendere più nel dettaglio il comportamento delle soluzioni stesse. È perciò rilevante il contrasto con la teoria delle equazioni di evoluzione lineari alle derivate parziali: per esse la tecnica basata sulla trasformata di Fourier ‒ introdotta per risolvere l'equazione lineare di propagazione del calore ‒ fornisce una metodologia trasparente, che permette di interpretare l'evoluzione temporale delle soluzioni in termini di velocità di fase, dispersione, velocità di gruppo. L'interesse per l'equazione KdV è rifiorito soltanto negli anni Sessanta del XX sec., non tanto nel campo dell'idrodinamica quanto in fisica dei plasmi e come conseguenza della sua connessione con il paradosso di Fermi, Pasta e Ulam.
Cenni storici
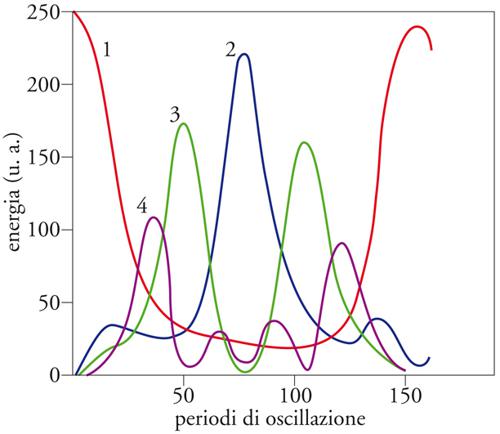
Intorno al 1950 cominciarono a essere disponibili per il calcolo scientifico i calcolatori elettronici, mediante i quali fu possibile condurre un esperimento numerico che portò a un risultato inatteso, noto con il nome di paradosso di Fermi, Pasta e Ulam. Nello studio di una catena unidimensionale di oscillatori accoppiati con i primi vicini in maniera non lineare (quadratica o cubica) condotto con tecniche di integrazione numerica, sulla base di concetti fondamentali della meccanica statistica ‒ quali il principio di equipartizione dell'energia ‒ ci si attendeva un moto sempre più stocastico, con la comparsa di componenti di frequenza via via più alta e una diffusione dell'energia su di esse. L'esperimento numerico mostrò invece che, se si partiva da una configurazione iniziale in cui l'energia era tutta concentrata nel modo normale di oscillazione più basso, a un certo istante si verificava un'inattesa ricorrenza: l'energia stessa tornava quasi del tutto sul modo iniziale, sebbene per tempi più brevi essa avesse mostrato la tendenza a ripartirsi negli altri modi normali (fig. 2). Nel tentativo di giustificare questo risultato, Martin D. Kruskal fu condotto allo studio dell'equazione KdV, che rappresenta un'approssimazione continua nel caso quadratico per la catena di oscillatori analizzata da Enrico Fermi, John Pasta e Stanislaw M. Ulam; tale equazione d'altra parte interviene nella descrizione di alcuni fenomeni di instabilità del plasma, il cui studio frattanto aveva acquisito grande importanza nel tentativo di realizzare la fusione nucleare controllata. La ripresa di interesse per l'equazione KdV portò a ulteriori importanti scoperte e invenzioni, compresa l'introduzione del concetto di solitone.
L'equazione KdV ammette soluzioni che hanno la particolarità di essere localizzate, possedere una forma ben definita e viaggiare con velocità costante. Si supponga ora di avere inizialmente una condizione in cui due configurazioni siffatte sono localizzate intorno a due punti molto lontani l'uno dall'altro e hanno velocità caratteristiche che le portano a sovrapporsi (basta che la configurazione inizialmente localizzata più a sinistra si muova verso l'altra e abbia velocità maggiore). È allora chiaro che, fino a quando le due onde localizzate sono abbastanza distanti da non interferire, entrambe viaggeranno con velocità costante e senza mutare forma; successivamente però le due configurazioni si sovrapporranno, magari perdendo completamente la loro identità, e per un certo intervallo di tempo il profilo potrà registrare un solo massimo anziché due. Ancora una volta mediante un esperimento numerico, si è scoperto tuttavia che le due onde riacquistano sempre la loro identità dopo la collisione. Quest'ultima provoca infatti soltanto un loro spostamento rispetto alla posizione che avrebbero avuto se avessero continuato a viaggiare indisturbate: dopo l'urto, la soluzione dell'equazione KdV rappresenta nuovamente un profilo che è la somma delle medesime due onde localizzate iniziali, ciascuna viaggiante con la propria velocità caratteristica. In questo modo, avendo avuto luogo uno scavalcamento ed essendosi invertito l'ordine delle due onde, esse si allontanano indefinitamente, così come prima andavano avvicinandosi. È il caso di sottolineare che questo comportamento è assai sorprendente: molte altre equazioni analoghe alla KdV ammettono soluzioni del tipo onda solitaria, ma nel loro caso una collisione dà luogo a una fenomenologia assai più complessa.
Il concetto di solitone, così come il termine usato per designarlo, furono introdotti nel 1965 da Norman Zabusky e Kruskal per indicare le entità localizzate che si manifestano come soluzioni dell'equazione KdV (e di altre equazioni speciali) la cui peculiarità è di uscire inalterate dalle collisioni; ciò suggerisce che esse conservino sempre una loro esistenza e identità anche quando, durante l'urto, se ne perde ogni traccia visibile. Oltre a porre in rilievo tutto ciò, il termine solitone è coniato in analogia con i nomi delle particelle elementari: elettrone, positrone, e così via. La rilevanza dal punto di vista applicativo e la fenomenologia connessa motivarono lo studio dell'equazione KdV da parte di Clifford S. Gardner, John M. Greene, Kruskal e Robert M. Miura, un gruppo di fisici teorici presso il grande laboratorio di fisica del plasma e per la fusione di Princeton. Cominciarono così a emergere altre rimarchevoli proprietà dell'equazione, a cominciare dall'esistenza di un numero infinito di costanti del moto: alcune grandezze costruite a partire da una soluzione qualunque dell'equazione KdV risultano costanti al trascorrere del tempo, nonostante la soluzione stessa vari con esso. La scoperta di gran lunga più importante fu però, nel 1967, quella del metodo di risoluzione cosiddetto della trasformata spettrale o della diffusione inversa. Esso, oltre a dare conto di numerose proprietà peculiari dell'equazione KdV, chiarisce la fenomenologia associata ai solitoni: questi ultimi compaiono non solamente come soluzioni speciali (la cui forma analitica è ora nota esplicitamente), ma rappresentano una componente identificabile con precisione della generica soluzione dell'equazione KdV, corrispondente a una larga classe di condizioni iniziali. All'estensione delle classi di equazioni risolubili mediante questa tecnica è stata dedicata un'intensa e fruttuosa attività di ricerca, che ha anche permesso di ottenere risultati inediti. Citiamo come esempio le equazioni non lineari di evoluzione, con solitoni che si muovono con velocità variabile nel tempo come particelle sottoposte a forze (bumeroni, trapponi, zumeroni), e la risolubilità mediante trasformata spettrale di equazioni che non possiedono alcuna soluzione di tipo solitonico come la cosiddetta equazione KdV cilindrica, di interesse applicativo nella fisica dei plasmi e della fusione. Proprio per questa ragione, non ci si sarebbe aspettati a priori che fossero trattabili con queste tecniche. Nei paragrafi successivi saranno descritte la tecnica della trasformata spettrale e la fenomenologia solitonica, usando come principale riferimento l'equazione KdV. Ci avvarremo dell'analogia fra la tecnica della trasformata spettrale, indicata per risolvere alcune classi di equazioni non lineari di evoluzione, e quella della trasformata di Fourier, adatta alla risoluzione di equazioni lineari di evoluzione.
Soluzione di equazioni lineari di evoluzione mediante la trasformata di Fourier
Si consideri l'equazione di evoluzione (alle derivate parziali):
[3] formula
dove ω(z) è un polinomio e i è l'unità immaginaria (i2=−1). Un problema tipico della fisica matematica e della matematica applicata è quello in cui la funzione u è assegnata all'istante iniziale,
[4] u(x, 0) = u0(x)
e se ne studia la successiva evoluzione (problema di Cauchy). Si assumerà sempre che la funzione incognita u(x,t) sia definita per ogni valore della variabile spaziale x e si annulli (abbastanza rapidamente) per x→±∞. La soluzione del problema si ottiene introducendo la trasformata di Fourier (nella variabile x) della u(x,t) mediante le formule
che stabiliscono una corrispondenza biunivoca fra la funzione u(x,t) e la sua trasformata di Fourier û(x,t). L'utilità di questa trasformazione è data dal fatto che all'equazione [3] per la u(x,t) corrisponde per la û(x,t) la semplice
[7] ût(k, t) = − iω(k)û(k, t)
che può essere immediatamente integrata. Il risultato è
[8] ût(k, t) = û0(k)exp[− iω(k)t]
dove
[9] formula.
La formula finale, che riassume in modo compatto il risultato,
[10] formula
indica chiaramente come l'evoluzione temporale della u(x,t) sia determinata dalla funzione di dispersione ω(k). La tecnica di risoluzione si fonda, dunque, sulla possibilità di scomporre la funzione u(x,t) nelle sue componenti di Fourier, û(k,t)exp(ikt), e sul fatto che, quando la u(x,t) evolve secondo l'equazione [3] alle derivate parziali, lineare e a coefficienti costanti, le sue componenti di Fourier subiscono semplicemente una traslazione uniforme, ciascuna con la propria velocità di fase ω(k)/k, secondo la [10]. Il fatto che, se si eccettua il caso ω(z)=cz, la velocità di fase vari al variare di k dà luogo al fenomeno della dispersione; sicché una soluzione (ossia un pacchetto d'onde), la cui trasformata di Fourier sia concentrata intorno al valore k0, tende, almeno per tempi grandi, a viaggiare con velocità di gruppo ω′(k0) (ω′(z)≡dω(z)/dz) e a disperdersi (nel caso di una sola dimensione spaziale, il suo massimo modulo va diminuendo proporzionalmente a 1/√t).
La tecnica di risoluzione della [3] mediante la trasformata di Fourier, anche se non sempre può essere implementata esplicitamente ‒ in quanto non è detto che gli integrali [5] e [6] possano essere calcolati in modo esplicito ‒ permette di comprendere come si comportino qualitativamente le soluzioni. È importante osservare che l'evoluzione temporale determinata dalla [3] è molto più semplice nello spazio di Fourier (vale a dire per la funzione u^ (k,t)) che non nello spazio delle configurazioni (ossia per la funzione u(x,t)), ancorché la corrispondenza biunivoca stabilita dalla [5] e dalla [6] renda le due rappresentazioni equivalenti. È per questo motivo che è preferibile ricondurre ogni tentativo di studiare un fenomeno schematizzato mediante la [3] al contesto dello spazio di Fourier, in cui è k la variabile indipendente, anziché porsi nello spazio delle configurazioni, con la variabile x.
L'equazione di Korteweg-de Vries
Nell'illustrare la teoria dei solitoni, si prende in considerazione tipicamente ‒ anche per motivi storici ‒ l'equazione KdV. Il fatto che essa sia del primo ordine nella derivata rispetto al tempo, e che pertanto non sia invariante rispetto al verso in cui il tempo scorre, trae origine dal fatto che essa descrive (in modo approssimato, e in un appropriato sistema di riferimento in moto uniforme) soltanto il comportamento di quella componente delle onde di superficie in un canale poco profondo che si propaga, complessivamente, in un solo verso. Abbiamo già introdotto la soluzione della KdV rappresentata da un solitone, che, come risulta chiaro, corrisponde piuttosto fedelmente alla descrizione di Scott Russell riportata in apertura; si immagini in particolare che la u(x,t), cambiata di segno, rappresenti l'altezza del pelo dell'acqua misurata, nel punto x e al tempo t, rispetto al livello del fluido in quiete. Pur essendo la [2] una soluzione particolare della [1], vedremo che contributi dello stesso tipo sono presenti nella generica soluzione dell'equazione KdV [1], in un senso che preciseremo. È opportuno mettere in evidenza che, a causa del fenomeno della dispersione, nessuna equazione lineare del tipo [3] ‒ a eccezione della banale equazione del primo ordine ut+vux=0, con soluzione u(x,t)=u(x−vt,0) ‒ può avere soluzioni che traslano senza cambiare di forma, come accade invece per la [2]. Per l'esistenza del solitone svolge dunque un ruolo essenziale la non linearità. In effetti, è lecito considerare che la soluzione [2] corrisponda a un preciso equilibrio tra gli effetti del termine dispersivo uxxx e quelli del termine non lineare uux nella [1]; se il termine non lineare fosse assente, il massimo modulo della soluzione tenderebbe ovunque a zero per t → ∞, mentre, se mancasse il termine dispersivo, la soluzione potrebbe dar luogo a una singolarità nella derivata (detta shock) entro un tempo finito.
La trasformata spettrale
Il problema spettrale di Schrödinger
Partiremo dal problema spettrale caratterizzato dall'equazione lineare di Schrödinger unidimensionale e indipendente dal tempo, che scriveremo
[11] − ψxx(k, x)+ u(x)ψ(k, x) = k2ψ(k, x).
Faremo sempre l'ipotesi che la funzione u(x) (il potenziale) si annulli abbastanza rapidamente per x → ±∞. È bene precisare che, sebbene la terminologia vi si richiami, le considerazioni che seguono sono del tutto indipendenti dal significato fisico dell'equazione di Schrödinger, usata solamente come prototipo di un problema spettrale del tipo Sturm-Liouville. Lo spettro dell'operatore differenziale a primo membro della [11] è generalmente composto da due parti: una continua, corrispondente a tutti i valori reali non negativi di k2, e un eventuale numero finito di autovalori discreti, corrispondenti a valori negativi di k2. Allo spettro continuo sono associate le due funzioni R(k) e T(k) ‒ rispettivamente coefficiente di riflessione e di trasmissione ‒ definite univocamente in base al comportamento della soluzione della [11], caratterizzata a sua volta dalle relazioni asintotiche
[12] formula,
[13] formula,
(la seconda individua la ψ(k,x) a meno di una costante moltiplicativa, fissata dalla condizione che, nella prima relazione, il coefficiente del primo termine a secondo membro valga esattamente 1; si ricordi che stiamo considerando il caso di k2>0, ossia k reale e, per convenzione, positivo). Allo spettro discreto si associano le autofunzioni normalizzate e reali ψ(ipn,x),
[14] formula
dove k2=−pn2 sono gli autovalori discreti reali e negativi, che in meccanica quantistica corrispondono a stati legati. Queste autofunzioni definiscono le costanti reali e positive ϱn, per il tramite della relazione asintotica
[15] formula.
Si definisce ora trasformata spettrale della funzione u(x) l'insieme di dati
[16] S = {R(k), −∞ 〈 k 〈 +∞; pn, ϱn, n =1, 2, ..., N}
dove N indica il numero degli autovalori discreti e, per convenzione, pn>0. Tale definizione è motivata dall'esistenza di una corrispondenza biunivoca tra la funzione u(x) e la sua trasformata spettrale S: in effetti, dalle equazioni già scritte risulta chiaro che u(x) determina univocamente S per il tramite della soluzione del problema spettrale diretto, caratterizzato dalle [11]-[13], laddove la determinazione univoca di u(x) da S equivale alla soluzione del problema spettrale inverso. In questo secondo caso si procede come segue. Data S, si costruisce la funzione
[17] formula
si considera quindi l'equazione di Gelfand-Levitan-Marcenko
[18] formula
che determina univocamente la funzione K(x,x′) a partire dalla M(x); infine, dalla K(x,x′) si ottiene la u(x) mediante la semplice formula
[19] formula
È importante osservare che vi è una diretta connessione fra la trasformata spettrale e la trasformata di Fourier. Nel limite di campi deboli, infatti, vale a dire se la funzione u(x) è talmente piccola che si può trascurare ogni effetto non lineare ‒ ivi compresa l'esistenza dello spettro discreto ‒ la [17] e la [18] implicano
[20] formula,
[21] K(x, x′) ∼ −M(x+x′)
sicché dalla [19] segue
[22] formula
dove û(k)è la trasformata di Fourier della u(x) [5]. Ecco dunque che la trasformata spettrale ‒ che in questo limite si riduce alla funzione R(k) ‒ si identifica essenzialmente, a meno di trasformazioni banali, con la trasformata di Fourier. La trasformata spettrale può essere considerata quindi come una generalizzazione non lineare della trasformata di Fourier, alla quale si riduce nel limite di campi deboli, in cui siano trascurati tutti gli effetti non lineari.
Osserviamo, infine, che i risultati qui descritti suggeriscono un ruolo speciale per quelle funzioni u(x) la cui trasformata spettrale è particolarmente semplice. In particolare, è possibile determinare esplicitamente la classe delle funzioni u(x) la cui trasformata spettrale contiene N autovalori discreti, caratterizzati dai 2N parametri pn e ϱn, e un coefficiente di riflessione identicamente nullo, R(k)=0: in tal caso l'equazione [18] si può risolvere esplicitamente, poiché il nucleo M(x+x′) è separabile (e di rango N). Particolarmente semplice e importante è la funzione u(x) la cui trasformata spettrale contiene un solo autovalore discreto (caratterizzato dai parametri positivi p e ϱ) e coefficiente di riflessione nullo, R(k)=0:
[23] formula.
Evoluzione temporale e classe delle equazioni integrabili
Consideriamo una funzione u(x,t) che dipenda anche dal tempo t. La corrispondente trasformata spettrale, naturalmente, dipenderà a sua volta dal tempo: S=S(t). Si assuma ora che la funzione u(x,t) soddisfi l'equazione di evoluzione
[24] ut(x, t) = α(Ḻ)ux(x, t)
dove α(z) è un polinomio in z e Ḻ denota un operatore integro-differenziale, dipendente dalla funzione u(x,t), il cui effetto su una funzione F(x,t) (nei casi in cui la seguente formula ha senso) è
[25] formula.
Si può allora dimostrare che la trasformata spettrale S(t) evolve in modo assai semplice: il coefficiente di riflessione R(k,t) evolve secondo l'equazione differenziale alle derivate ordinarie
[26] Rt(k, t) = 2ikα(−4k2)R(k, t)
dove gli autovalori pn rimangono costanti (e ovviamente il loro numero non cambia) e i coefficienti ϱn evolvono a loro volta secondo l'equazione differenziale
[27] ϱ.n(t) = −2pnα(4pn2) ϱn(t).
Abbiamo qui indicato con un punto sovrapposto la derivata rispetto al tempo. Queste equazioni differenziali possono essere immediatamente integrate, per ottenere
[28] R(k, t) = R(k, 0)exp[2ikα(−4k2)t]
[29] ϱn(t) = ϱn(0)exp[−2pnα(4pn2)t].
Si noti che il fatto che gli autovalori pn non variano nel tempo indica che, quando il potenziale u(x,t) evolve nel tempo secondo la [24], gli autovalori dell'operatore lineare differenziale di Schrödinger −∂2/∂x2+u(x,t) restano invariati: siamo dunque in presenza di un'evoluzione isospettrale di tale operatore. Questa osservazione svolge un ruolo fondamentale in altre formulazioni di questi e di analoghi risultati. La [24] è un'equazione, o meglio, una classe di equazioni non lineari di evoluzione per la funzione u(x,t), ciascuna delle quali corrisponde a una specifica scelta del polinomio α(z). È possibile dimostrare che, grazie alla definizione [25] dell'operatore differenziale Ḻ ‒ e nonostante la presenza in essa dell'operatore integrale ‒ la [24] è una pura equazione differenziale; infatti, qualunque potenza dell'operatore Ḻ applicata a ux(x,t) produce soltanto una combinazione non lineare della u(x,t) stessa e delle sue derivate rispetto a x: tutte le integrazioni si possono effettuare in modo esatto. In particolare
[30] Ḻux(t) = uxxx − 6uxu = (uxx−3u2x)x
[31] Ḻ2ux = (uxxxx−10uxxu−5u2x+10u3)x.
In conclusione, se u(x,t) evolve secondo l'equazione non lineare alle derivate parziali [24], la corrispondente trasformata spettrale evolve in modo lineare e assai semplice, come specificato dalle [26]-[29]. L'analogia di tale formalismo con quello delle equazioni di evoluzione lineari, basato sulla trasformata di Fourier, è del tutto evidente. È opportuno richiamare l'attenzione anche sul fatto che tanto il problema spettrale diretto quanto quello inverso comportano la risoluzione di equazioni lineari: l'equazione di Schrödinger [11] nel primo caso, nel secondo l'equazione di Gelfand-Levitan-Marcenko [18]. La più semplice equazione non banale della classe [24] corrisponde alla scelta α(z)=−z e coincide, per l'appunto, con l'equazione KdV [1]. Le formule corrispondenti per l'evoluzione temporale della trasformata spettrale sono dunque
[32] R(k, t) = R(k, 0)exp[−(2ik)3t]
[33] ϱn(t) = ϱn(0)exp[(2p3n)t].
Solitoni e solitroni
La conclusione più rilevante che si evince da quanto appena detto è che, come nella risoluzione di equazioni di evoluzione lineari mediante trasformata di Fourier, anche per le equazioni della classe [24], l'evoluzione temporale assume una forma assai più semplice nello spazio delle variabili spettrali che non nello spazio delle configurazioni. Per comprendere il comportamento delle soluzioni, e con esso i fenomeni naturali che tali equazioni schematizzano, occorre pertanto rifarsi alle proprietà del problema spettralee distinguere le diverse componenti di ogni soluzione. Nell'effettuare succintamente tale analisi, per semplicità faremo riferimento prevalentemente all'equazione KdV [1], sebbene le considerazioni che proporremo siano valide per l'intera classe [24], e per una classe persino più vasta.
Lo spettro continuo
La distinzione principale che va fatta riguardo alla trasformata spettrale è tra la componente associata allo spettro discreto e quella associata al continuo. Consideriamo anzitutto il continuo: il contributo alla u(x,t) dovuto a questa componente è chiamato generalmente sfondo (background). Esso è presente anche se tutti gli effetti non lineari sono trascurabili, come avviene per esempio nell'approssimazione di campi deboli: in tal caso (si veda anche la trattazione che segue l'equazione [19]), il comportamento della soluzione corrisponderà a quello delle soluzioni dell'equazione lineare ottenuta trascurando tutte le parti non lineari. Per esempio, nel caso dell'equazione KdV, l'equazione linearizzata si scrive
[34] ut(x, t) + uxxx(x, t) = 0
ovverosia
[35] formula
con
[36] ω(k) = −k3
il comportamento delle sue soluzioni sarà dunque caratterizzato dal fenomeno della dispersione, regolato dalla [36], cui è associata la velocità di gruppo
[37] vg = ω′(k) = −3k2
Questa velocità è sempre negativa, o al più nulla; asintoticamente, le soluzioni della [34], oltre a delocalizzarsi e disperdersi, tenderanno pertanto a sfuggire verso sinistra, vale a dire verso i valori negativi delle x. Più generalmente, come conseguenza della definizione [25] dell'operatore L, nel limite in cui tutti gli effetti non lineari sono trascurati, la classe [24] di equazioni non lineari si riduce precisamente alla classe [3] di equazioni lineari, con l'identificazione
[38] ω(z) = −zα(−z2)
se dunque α(y) è un polinomio in y di grado m, ω(z) è un polinomio di grado dispari 2m+1. Si noti la coerenza fra la validità del regime lineare nel caso di campo debole e il fatto che il fenomeno della dispersione assicura per l'appunto che l'evoluzione temporale causi ovunque un affievolimento locale del campo.
Lo spettro discreto: i solitoni
Gli effetti essenzialmente non lineari si manifestano invece nella componente associata alla parte con spettro discreto della trasformata spettrale, che dà conto della comparsa dei solitoni. Ne analizziamo il comportamento cominciando dal caso più semplice, una soluzione la cui trasformata spettrale sia caratterizzata dalla presenza di un solo autovalore discreto e da un coefficiente di riflessione nullo; condizione che, se è valida inizialmente, resta valida sempre. La forma esplicita della corrispondente soluzione nello spazio delle configurazioni segue dalla [23], dalla [28] e dalla [29]:
[39] formula[40]
Questa soluzione descrive, dunque, un'onda localizzata che si muove senza cambiare forma; la velocità v è legata al parametro p, che dipende da altezza e larghezza dell'onda, mediante la formula [40], in cui compare la funzione α(z) che caratterizza la particolare equazione non lineare di evoluzione della classe [24]. Ecco dunque il solitone!
Nel caso dell'equazione KdV che corrisponde ad α(z)=−z, l'espressione della velocità [40] diventa
[41] v = 4p2.
In questo caso, dunque, il solitone si muove nel verso positivo dell'asse x, con una velocità che è direttamente proporzionale alla propria altezza. Oltre alla soluzione solitonica testé descritta, vi sono soluzioni multisolitoniche, la cui trasformata spettrale è ancora caratterizzata dall'annullarsi del coefficiente di riflessione R(k,t), mentre la parte di spettro discreto contiene un numero finito N di autovalori, ciascuno dei quali dà origine a un diverso solitone. Nel caso dell'equazione KdV, tale soluzione si riduce essenzialmente, tanto nel passato quanto nel futuro remoti, alla somma di N solitoni ben separati: nel remoto passato essi sono ordinati, in modo che i più grandi siano più a sinistra; nel remoto futuro, viceversa, i più grandi, e perciò i più veloci, si trovano più a destra. L'unico effetto dello scavalcamento è l'aver determinato uno sfasamento ‒ calcolabile in modo esplicito ‒ rispetto alla posizione che ciascun solitone avrebbe avuto se non ne avesse scavalcato altri, o non fosse stato da altri scavalcato.
Accenniamo, sempre con riferimento all'equazione KdV, al comportamento qualitativo di una soluzione generica, la cui trasformata spettrale conterrà dunque tanto un contributo di spettro continuo (coefficiente di riflessione R(k,t) non nullo) quanto uno di spettro discreto; l'entità di tali contributi è chiaramente fissata dalle condizioni iniziali (si osservi che soltanto la fase del coefficiente di riflessione varia nel tempo, laddove il suo modulo rimane costante, [32]). Tale comportamento si ottiene combinando quelli fin qui descritti. Nel remoto futuro, dunque, ogni soluzione si scomporrà in un certo numero di solitoni, che si allontanano verso destra, e in un contributo di sfondo, che tende a delocalizzarsi e a dirigersi nel verso opposto; il numero e le proprietà dei solitoni sono determinati dalle caratteristiche della parte di spettro discreto della trasformata spettrale corrispondente alle condizioni iniziali.
È opportuno sottolineare, infine, che la classe di equazioni alle derivate parziali non lineari che posseggono soluzioni che viaggiano senza cambiare di forma è alquanto vasta. Si consideri per esempio la più generale equazione di evoluzione
[42] ut(x, t) = F[u(x, t), ux(x, t), uxx(x, t), ...].
Ebbene, è chiaro che essa ammetterà una soluzione localizzata, del tipo
[43] u(x, t) = f(x − vt)
che descrive per l'appunto un'onda che trasla con velocità v, se l'equazione alle derivate ordinarie
[44] vf′+F(f, f′, f″, ...) = 0
ammette ‒ magari per qualche opportuno valore di v solamente ‒ una soluzione f(y) che è regolare per ogni valore reale di y e che si annulla per y → ±∞. Non si tratta, evidentemente, di una condizione molto restrittiva. In generale, però, onde solitarie di questo tipo, se collidonol'una con l'altra, danno luogo a una fenomenologia assai più complicata.
I solitroni
Alcuni puristi desidererebbero che il termine solitone fosse riservato esclusivamente a quegli oggetti che subiscono solamente collisioni elastiche, in cui dopo l'urto sono presenti soltanto gli stessi oggetti che erano presenti prima dell'urto (come avviene per le soluzioni delle equazioni della classe [24] e, in particolare, dell'equazione KdV); si ritiene, del resto, che tutte le equazioni non lineari di evoluzione che danno luogo a tale fenomenologia solitonica siano anche integrabili mediante una qualche variante del metodo della trasformata spettrale. Questi stessi studiosi suggerirebbero di usare invece l'espressione onda solitaria, oppure solitrone (dall'assonanza con i nomi delle particelle elementari: elettrone, positrone, ecc.), per identificare qualunque soluzione di un'equazione di evoluzione non lineare alle derivate parziali, che abbia la caratteristica di mantenersi localizzata nel tempo e di comportarsi in definitiva come una particella. Secondo tale convenzione, tutti i solitoni sarebbero dunque solitroni. Non varrebbe però il viceversa, in quanto il termine solitone resterebbe riservato a quei casi speciali nei quali queste soluzioni localizzate hanno la notevole proprietà di subire soltanto collisioni elastiche; a quei casi, dunque, in cui le equazioni di evoluzione sono risolubili (ossia esattamente linearizzabili) mediante la tecnica della trasformata spettrale o un metodo analogo. Occorre però avvertire che queste convenzioni sono largamente disattese, sicché frequentemente si usa, nei più svariati campi applicativi, il termine solitone per denotare qualunque ente esteso che si mantenga localizzato e abbia una qualche persistenza temporale.
Leggi di conservazione e altre equazioni risolubili
Le equazioni non lineari di evoluzione della classe [24] hanno molte altre notevoli proprietà. Ne ricorderemo qui soltanto una: l'esistenza di un numero infinito di leggidi conservazione. Una formula compatta per esprimere queste quantità conservate, indipendenti dal tempo, è
[45] formula,
dove l'operatore integro-differenziale è definito dalla [25] e il fattore moltiplicativo è convenzionale. Nonostante la presenza dell'operatore integrale in questa definizione di Ḻ, e nonostante compaia esplicitamente la variabile x nell'espressione su cui agisce l'operatore Ḻ a secondo membro della [45], queste quantità conservate risultano tutte formulate come un singolo integrale di un'espressione non lineare della funzione u e delle sue derivate, senza che la variabile x compaia esplicitamente; per esempio,
[46] formula.
Se la tecnica della trasformata spettrale avesse permesso di risolvere soltanto l'equazione KdV, o solamente l'intera classe di equazioni non lineari di evoluzione [24], la sua importanza sarebbe stata modesta. Tuttavia, ricorrendo a tecniche analoghe, numerose altre equazioni non lineari di evoluzione, comprese alcune di grande interesse applicativo e teorico, sono risolubili esattamente. Ne sono esempi la cosiddetta equazione non lineare di Schrödinger,
[47] iut(x, t) + uxx(x, t) + g∣u(x, t)∣2 u(x, t) = 0
quella detta equazione di seno-Gordon, che si presenta in due versioni,
[48] utt(x, t) − uxx(x, t) = g sen[u(x, t)]
uξτ(ξ, τ) = g sen[u(ξ, τ)]
l'equazione KdV modificata,
[49] ut(x, t) + uxxx(x, t) − 6ux(x,t)u2(x, t) = 0.
e molte altre; un elenco senza pretese di completezza, pubblicato nel 1982, annovera trentasette equazioni risolubili, quasi tutte di notevole interesse applicativo o teorico.
L'equazione non lineare di Schrödinger descrive l'evoluzione di un campo complesso ed è particolarmente importante dal punto di vista applicativo, rivelandosi generalmente appropriata per descrivere l'evoluzione temporale di un'onda quasi monocromatica, che si propaghi in un mezzo debolmente lineare e dispersivo. Anche l'equazione di seno-Gordon è molto importante, sia per il suo interesse teorico, per esempio nella teoria delle superfici, sia come prototipo di equazione relativisticamente invariante; è quindi particolarmente appropriata come equazione-modello per lo studio, nel contesto della fisica delle particelle elementari, della teoria relativistica dei campi classici e quantistici. Oltre alle equazioni alle derivate parziali, vi sono anche importanti esempi di equazioni integro-differenziali risolubili con tecniche di questo tipo, nonché equazioni alle differenze finite, generalmente associate a una discretizzazione delle variabili spaziali e temporali, che sono risolubili attraverso un opportuno adattamento della tecnica della trasformata spettrale o delle altre tecniche usate per la risoluzione e lo studio delle equazioni alle derivate parziali. Concludiamo ricordando la possibilità ‒ ovviamente molto interessante dal punto di vista applicativo ‒ di studiare anche equazioni che non siano esattamente risolubili mediante queste tecniche, partendo dalla soluzione di un'equazione non lineare, ma risolubile con tecniche esatte, che assomigli a quella che si vuol studiare, e applicando poi tecniche perturbative.
Bibliografia
Calogero 1979: Calogero, Francesco, I solitoni, in: Enciclopedia della scienza e della tecnica, Milano, Mondadori, 1979.
Calogero 1989: Calogero, Francesco, Solitoni, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, 1989, VIII, pp. 978-991.
Calogero 1990: Calogero, Francesco, Why are certain nonlinear PDEs both widely applicable and integrable?, in: What is integrability?, edited by Vladimir E. Zakharov, Berlin-New York, Springer, 1990, pp. 1-62.
Calogero, Degasperis 1982: Calogero, Francesco - Degasperis, Antonio, Spectral transform and solitons: tools to solve and investigate nonlinear evolution equations, Amsterdam-Oxford, North-Holland, 1982.

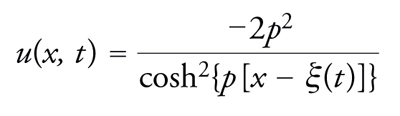
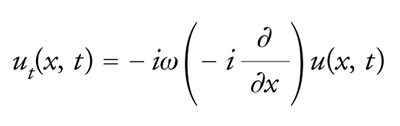
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/e/e3/FORM_Solitoni_form_05.jpg)
![[6]](https://images.treccani.it/ext-tool/intra/thumbs_medium/6/69/FORM_Solitoni_form_06.jpg)