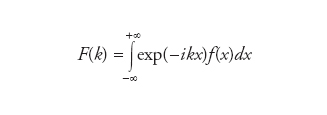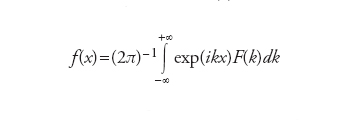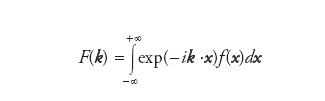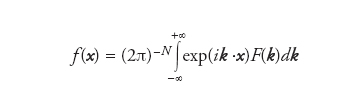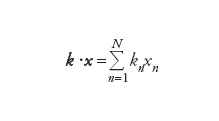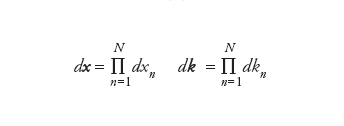spazio di Fourier
spazio di Fourier
La trasformata di Fourier F(k) di una data funzione f(x) definita sull’intero asse reale e che si annulla (abbastanza rapidamente) all’infinito, f(±∞)=0, si definisce come segue:
formula.
Questa formula – che determina una corrispondenza biunivoca fra la funzione f(x) e la sua trasformata di Fourier F(k) – ammette la seguente formula inversa:
[1b] formula
che ovviamente implica che a sua volta la F(k) si annulla asintoticamente, F(±∞)=0. Lo spazio di Fourier è per l’appunto lo spazio delle funzioni F(k), mentre talvolta lo spazio delle funzioni f(x) viene indicato come spazio delle configurazioni. Questo linguaggio è particolarmente usato in fisica, dove nell’ambito della meccanica quantistica la variabile x gioca generalmente il ruolo di variabile spaziale, laddove la variabile k ha corrispondentemente (in opportune unità adimensionali) il significato di impulso. La generalizzazione di queste considerazioni al caso multidimensionale è ovvia. In particolare in tale contesto le formule precedenti vengono rimpiazzate come segue:
[2a] formula
[2b] formula
dove x ≡(x1,...,xN) rispettivamente k≡(k1,...,kN) sono vettori a N dimensioni, il prodotto scalare k ∙x è definito nel modo consueto, ossia
[3] formula
e
[4] formula.
Osserviamo infine che l’introduzione del fattore (2π)−1 a secondo membro della [1b], e analogamente del fattore (2π)−N a secondo membro della [2b], è la convenzione generalmente (ma non universalmente) usata in fisica; in matematica si usa generalmente (ma non universalmente) la più simmetrica convenzione che introduce a secondo membro sia della [1a] sia della [1b] lo stesso fattore (2π)−1/2, e corrispondentemente a secondo membro sia della [2a] sia della [2b] lo stesso fattore (2π)−N/2.
→ Solitoni