podaria
Enciclopedia on line
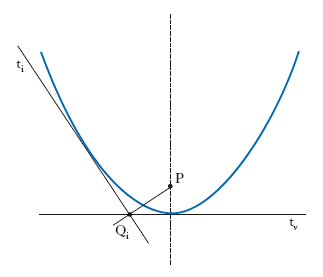
In geometria, p. (o pedale) di una curva piana rispetto a un punto P del suo piano è il luogo dei piedi Qi delle perpendicolari condotte da P alle tangenti ti alla curva; rispetto alla nuova curva, la primitiva si chiama allora antipodaria (o antipedale). Esempi: la p. di una parabola rispetto al suo fuoco è la tangente tv nel vertice (v. fig.); rispetto al suo vertice è una cissoide di Diocle; la p. di una circonferenza rispetto a un punto del suo piano (escluso il centro) è una lumaca di Pascal (➔ concoide).