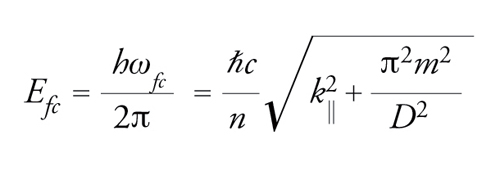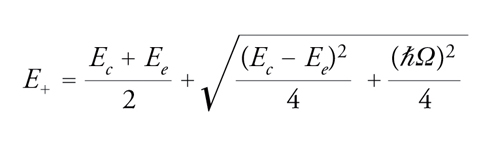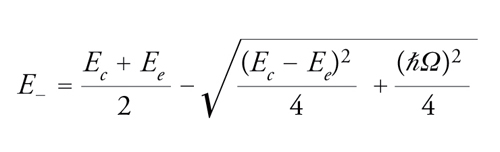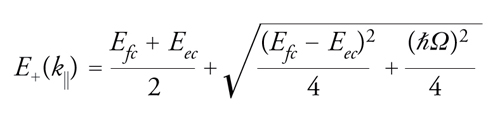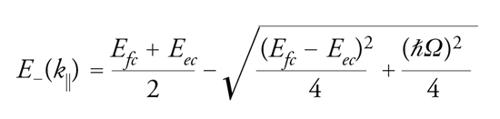Microcavità
Microcavità
Lo studio dell'interazione luce-materia ha da sempre richiamato l'attenzione degli scienziati, sia perché cruciale per la comprensione di molti fenomeni naturali sia perché utile per la realizzazione di innumerevoli dispositivi tecnologici. Sulla base dei principi della meccanica quantistica, si sono compresi i meccanismi microscopici che regolano l'emissione e l'assorbimento dei fotoni. Tali processi possono essere controllati modificando opportunamente gli stati elettronici dei materiali, come avviene in particolare nelle eterostrutture a semiconduttore utilizzate nell'ambito dell'optoelettronica. Tuttavia, oltre ai gradi di libertà dei mezzi materiali, si possono controllare anche quelli dei campi elettromagnetici al fine di condizionare opportunamente l'interazione luce-materia.
In questa prospettiva sono molto interessanti i sistemi a dimensionalità ridotta, in cui gli elettroni o i fotoni risultano confinati in un piano, lungo un filo o addirittura intorno a un punto. All'interno dei sistemi a dimensionalità ridotta, le microcavità sono risuonatori ottici di dimensioni micrometriche che confinano i modi propri di oscillazione del campo elettromagnetico (fotoni di cavità) su scale di dimensioni dell'ordine della lunghezza d'onda della luce.
La funzione essenziale di una microcavità è quella di produrre confinamento fotonico con la conseguente ristrutturazione della distribuzione spettrale e spaziale dei campi elettromagnetici al suo interno. Le geometrie impiegate variano molto a seconda che si vogliano ottenere fotoni di cavità bidimensionali (sistemi planari), unidimensionali (sistemi a filo) o totalmente confinati (sistemi a scatola), così come variano i tipi di specchi impiegati, che possono essere metallici o dielettrici.
Lo studio di sistemi a microcavità, i quali comprendono in una stessa struttura monolitica il materiale otticamente attivo e gli specchi responsabili per il confinamento della luce, consente di allargare le nostre conoscenze sulla interazione luce-materia, in particolare su aspetti dell'elettrodinamica quantistica e di migliorare le proprietà optoelettroniche alla base di dispositivi a stato solido quali: i diodi emettitori di luce (LED) e i diodi laser.
Configurazioni a microcavità planare sono utili per mirare l'efficienza di un LED aumentando la quantità di luce estratta dal dispositivo, che negli usuali diodi privi di microcavità è fortemente limitata per riflessione totale interna all'interfaccia tra il semiconduttore e l'aria (in assenza di speciali accorgimenti, l'efficacia di estrazione è tipicamente inferiore al 5%).
Nei LED a microcavità (MC-LED), una cavità con un leggero detuning verso il rosso della banda di emissione e uno specchio di moderata riflettività consentono di ottimizzare l'efficacia di estrazione della luce spontaneamente emessa raggiungendo facilmente valori dell'ordine del 20%. Per MC-LED da accoppiare in fibra ottica al fine di migliorare la concentrazione spettrale e angolare della luce emessa ortogonalmente alla microcavità può essere utile aumentare la riflettività dello specchio a multistrati dielettrici utilizzato, senza peraltro dover necessariamente raggiungere riflettività molto elevate.
Confinamento fotonico
Le microcavità più usate sono quelle planari, nelle quali due specchi piani e paralleli confinano tra di loro i fotoni di cavità che rimangono liberi di propagarsi solo lungo il piano della cavità. Tali sistemi (detti cavità di Fabry-Pérot) possono essere schematizzati in modo semplice. Infatti, nella direzione ortogonale agli specchi (l'asse della cavità), i campi elettromagnetici assumono configurazioni a onda stazionaria in quanto il campo elettrico polarizzato nel piano della cavità deve annullarsi in corrispondenza degli specchi, che per il momento possiamo considerare dei metalli perfetti. La distanza D tra gli specchi determina la distanza l tra due nodi adiacenti dell'onda stazionaria, disposti parallelamente agli specchi, in base alla relazione D=ml, dove m è un numero intero, tipicamente piccolo. Il caso m=1 corrisponde al modo elettromagnetico di energia più bassa, m=2, 3,… a modi di energia via via crescente. Infatti, l'energia di un fotone di cavità assume i valori dati dalla seguente relazione:
[1] formula,
dove k∣∣ è il vettore d'onda bidimensionale che varia con continuità corrispondentemente al moto libero dei fotoni lungo il piano della microcavità, n è l'indice di rifrazione del materiale che la riempie, c è la velocità della luce e h=2πℏℏ è la costante di Planck. Tale legge di dispersione, Efc=Efc(k∣∣), differisce da quella dei fotoni in un mezzo omogeneo non confinato, data semplicemente da E=ℏω=(ℏc/n)k, dove k è un vettore d'onda tridimensionale. In particolare, in una microcavità di spessore D esiste una frequenza di soglia ω0=(c/n)(π/D) al di sotto della quale non sono presenti fotoni.
La nuova legge di dispersione dovuta al confinamento della luce, implica dunque una significativa ristrutturazione della densità degli stati per unità di energia a disposizione dei campi elettromagnetici, che può risultare soppressa o esaltata rispetto a quella in assenza di confinamento. Anche la distribuzione spaziale dell'intensità dei campi elettromagnetici è alterata e risulta concentrata nelle regioni corrispondenti ai ventri delle onde stazionarie confinate nella microcavità a scapito delle regioni nodali.
Controllo dell'emissione spontanea
La ristrutturazione della distribuzione spettrale e spaziale dei campi elettromagnetici che abbiamo esemplificato per il sistema planare di una cavità di Fabry-Pérot ideale avviene con caratteristiche diverse in tutti i tipi di microcavità con effetti più pronunciati per il sistema a scatola, in cui le frequenze dei fotoni di cavità sono completamente discretizzate poiché non vi è propagazione libera in alcuna direzione. Il confinamento fotonico ha immediate e importanti implicazioni per l'interazione luce-materia in una microcavità in cui sia presente un materiale otticamente risonante, cioè in grado di assorbire (o emettere) fotoni di frequenza vicina a quella dei fotoni di cavità mediante la creazione (o distruzione) di un'eccitazione elettronica. Tali effetti già ampiamente dimostrati in fisica atomica, utilizzando in particolare fasci di atomi altamente eccitati (atomi di Rydberg) in volo attraverso cavità macroscopiche, sono stati più recentemente osservati anche nelle microcavità monolitiche a stato solido.
Il fenomeno più eclatante è quello del controllo dell'emissione spontanea: la ristrutturazione dei modi elettromagnetici può rallentare o accelerare il processo di decadimento radiativo di uno stato eccitato, rispettivamente sopprimendo o esaltando la densità degli stati fotonici a disposizione del fotone emesso. Per esempio, se un'eccitazione elettronica di energia ben definita è risonante con un modo fotonico completamente confinato in una cavità a scatola, il suo tempo di vita risulta dato da τ∼(nω/c)3(V/Q)τ0, dove τ0 è il tempo di vita naturale in assenza di confinamento fotonico, V è il volume della cavità e Q il suo fattore di qualità. Quest'ultimo è limitato, in quanto la riflettività degli specchi R non è perfetta, ed è dato da Q=ω/γ∝1/(1−R), dove ω è la frequenza del fotone di cavità e γ la sua incertezza, corrispondente al fatto che il fotone di cavità non vive indefinitamente a lungo, perché ha una possibilità, seppur piccola, di attraversare gli specchi che lo confinano. Pertanto, il tempo di decadimento τ diminuisce quanto più la cavità è piccola e quanto più il fattore di qualità è alto, cioè all'aumentare del confinamento del fotone di cavità in cui l'eccitazione elettronica decade (si parla in tal caso di effetto Purcell). Ciò rimane vero, tuttavia, purché l'energia di interazione luce-materia che determina l'accoppiamento tra l'eccitazione elettronica e il fotone di cavità in cui decade sia piccola rispetto alla larghezza di riga ℏγ di quest'ultimo (regime di accoppiamento debole).
L'effetto Purcell esemplifica i vantaggi di avere una microcavità che sia la più piccola possibile (quindi con dimensioni confrontabili con la lunghezza d'onda della luce risonante) e che abbia un elevato fattore di qualità (quindi con specchi molto efficienti). Questo importante fenomeno di elettrodinamica quantistica in cavità è stato recentemente osservato con un fattore τ0/τ≈10 in microcavità a scatola di forma cilindrica o a disco in cui il mezzo materiale otticamente risonante è costituito da nanocristalli semiconduttori (punti quantici autoorganizzati di InAs). In essi, il confinamento quantistico degli stati elettronici dà luogo a uno spettro discreto di transizioni in cui elettroni in uno stato eccitato decadono in uno stato non occupato di energia inferiore emettendo un fotone (ricombinazione radiativa elettrone-buca). Anche il fenomeno opposto, in cui il decadimento radiativo viene inibito quando la frequenza della transizione elettronica non è in risonanza con un modo della cavità, è stato similmente osservato. Il controllo dell'emissione spontanea è molto rilevante anche da un punto di vista tecnologico, per esempio per la realizzazione di laser a bassissima soglia e di dispositivi per l'emissione di fotoni singoli.
Dispositivi a microcavità
Oltre alla modifica della velocità di decadimento radiativo, altri effetti del confinamento fotonico riguardano la distribuzione angolare e spettrale della luce emessa e risultano rilevanti anche nel caso più comune delle microcavità planari. In particolare, assumendo che la luce provenga da un dipolo oscillante orientato nel piano della cavità, quando la frequenza di emissione è risonante con la frequenza del fotone di cavità, la distribuzione angolare della luce è fortemente concentrata nella direzione ortogonale alla cavità, direzione nella quale l'intensità cresce di un fattore proporzionale al fattore di qualità Q rispetto a quella emessa dallo stesso dipolo in assenza della cavità. Anche in presenza di una banda ampia di frequenze emesse, piuttosto che di un emettitore monocromatico, la cavità oltre a filtrare l'emissione riducendone la larghezza spettrale e angolare può aumentarne l'intensità soprattutto quando all'interno della banda di emissione cade la frequenza di un solo modo fotonico confinato.
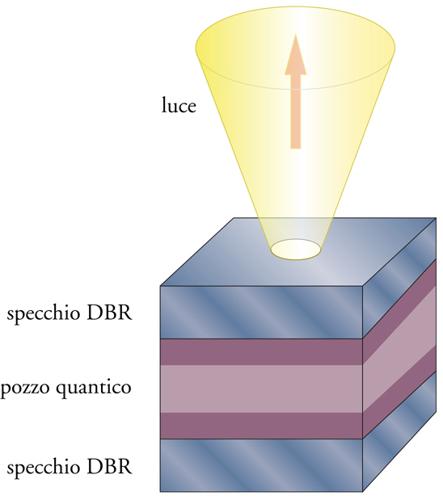
La ridistribuzione angolare e spettrale della luce emessa è alla base del funzionamento dei dispositivi optoelettronici a microcavità ritenuti oggigiorno più importanti, i VCSEL (Vertical cavity surface emitting laser), diodi laser semiconduttori a cavità verticale con emissione dalla superficie, che si sono diffusi a partire dagli anni Novanta. Nei VCSEL il mezzo attivo è tipicamente un pozzo quantico, cioè uno strato di materiale semiconduttore, posto all'interno di una microcavità planare di spessore confrontabile con la lunghezza d'onda della luce emessa, nel quale elettroni e buche elettricamente iniettati si raccolgono per ricombinarsi radiativamente. Tale cavità di Fabry-Pérot determina, come visto sopra, il modo fotonico confinato in cui viene emessa la luce laser, la quale infine fuoriesce attraverso gli specchi della cavità perpendicolarmente al pozzo quantico (fig. 2). Al contrario, i diodi laser semiconduttori tradizionali hanno una configurazione a guida d'onda in cui la luce si propaga lungo la regione attiva responsabile del guadagno ottico. In essi il modo fotonico in cui viene emessa la luce laser fuoriesce dai bordi della regione attiva, ottenuti troncando il dispositivo lungo piani cristallini paralleli e realizzando così una cavità longitudinale molto lunga rispetto alla lunghezza d'onda della luce emessa (edge emitting laser). Oltre a specifici vantaggi dovuti alla configurazione di microcavità verticale, quali la forma circolare con piccola divergenza del fascio emesso e la bassa corrente di soglia, i VCSEL ne presentano altri dovuti alla tecnica di costruzione; in particolare, essi hanno la possibilità di essere configurati in griglie bidimensionali (integrazione orizzontale) e incorporati in architetture optoelettroniche più complesse (integrazione verticale) a costi contenuti. A questo riguardo, le dimensioni laterali di un singolo laser possono essere ridotte fino a pochi μm, il che consente di abbassare la corrente di soglia a poche decine di μA e di ottenere griglie planari monolitiche contenenti milioni di dispositivi individuali.
Per quanto riguarda la microcavità di un VCSEL, il suo requisito fondamentale è quello di avere un fattore di qualità molto elevato, in quanto i fotoni devono essere in grado di attraversare il pozzo quantico moltissime volte per ottenere un guadagno ottico sufficiente prima di fuoriuscire dalla cavità. Gli specchi devono avere valori di riflettività superiori al 99%, il che non è ottenibile con gli usuali specchi metallici a causa del loro residuo assorbimento. Sono quindi utilizzati specchi a multistrati dielettrici, in cui si alternano periodicamente due dielettrici trasparenti con indici di rifrazione diversi e con spessori ottici pari a un quarto della lunghezza d'onda del fotone di cavità. In tali specchi DBR (Distributed Bragg reflector, riflettore di Bragg distribuito), tutte le riflessioni, a ogni interfaccia del multistrato, interferiscono costruttivamente producendo una riflettività complessiva quasi totale.
La riflettività a incidenza normale di uno specchio DBR è data da R=1−4(n1/n2)2N, dove n1 e n2 sono, rispettivamente, il minore e il maggiore degli indici di rifrazione dei due materiali costituenti il multistrato dielettrico (che tipicamente non sono molto diversi tra loro), e N è il numero di periodi che lo compongono, tipicamente pari a poche decine. Uno specchio DBR ha una riflettività molto elevata per una porzione di angolo solido centrato intorno all'incidenza normale e una banda di frequenze attorno a quella corrispondente alla condizione di quarto d'onda, la cui ampiezza dipende dal contrasto degli indici di rifrazione.
Dal punto di vista tecnologico, la realizzazione degli specchi DBR è spesso un fattore critico, soprattutto quando si passa dai VCSEL basati su AlGaAs/GaAs con lunghezze d'onda di emissione intorno a 0,85 μm a quelli basati su InGaAsP/InP con emissione a lunghezze d'onda maggiori, intorno a 1,3 μm. Per questi ultimi, sono necessari specchi DBR di notevole spessore in quanto i materiali con cui possono essere costruiti hanno un piccolo contrasto di indice di rifrazione. Ciò comporta, oltre a peggiori proprietà di dissipazione del calore, anche costi di produzione molto più elevati in quanto tutto il dispositivo, specchi DBR compresi, è cresciuto tramite tecniche di epitassia da fasci molecolari.
Regime di accoppiamento forte
Tutti gli effetti di confinamento fotonico dovuti a una microcavità del tipo di quella di cui abbiamo finora parlato riguardano il regime di accoppiamento debole ‒ il più comune ‒, in cui l'interazione luce-materia può essere considerata come una perturbazione. È tuttavia di grande interesse anche il regime opposto, di accoppiamento forte, in cui l'interazione luce-materia causa un completo mescolamento tra le eccitazioni elettroniche e i fotoni di cavità, tanto che essi perdono la loro individualità. Quando la frequenza Ω corrispondente all'energia di interazione tra un'eccitazione elettronica e un fotone di cavità (frequenza di Rabi) è maggiore delle larghezze di riga del fotone di cavità e dell'eccitazione elettronica, il trasferimento di energia tra l'una e l'altro non è più un processo di decadimento irreversibile. Infatti, il fotone di cavità vive sufficientemente a lungo da poter cedere nuovamente la sua energia al mezzo materiale con cui è in risonanza, rieccitandolo. A differenza di un normale processo di riassorbimento, tuttavia, tale processo è del tutto coerente in quanto nel regime di accoppiamento forte sia l'eccitazione elettronica sia il fotone di cavità mantengono la propria coerenza di fase più a lungo del tempo richiesto per completare un ciclo di scambio di energia (detto periodo di Rabi). La conseguenza di ciò è che, dal punto di vista quantistico, gli stati stazionari del sistema non sono più le eccitazioni elettroniche e i fotoni di cavità, tra loro separati, bensì nuove entità formate da una sovrapposizione coerente delle due. Queste ultime sono dette polaritoni di cavità e si comportano come particelle bosoniche.
Quando un fotone di cavità di energia Ec e un'eccitazione elettronica di energia Ee∼Ec ‒ ciascuna corrispondente a uno stato di larghezza di riga trascurabile e completamente confinato (come in un sistema a scatola) ‒ sono accoppiati da un'interazione ℏℏΩ, dal loro mescolamento si formano due nuovi stati, detti polaritone di cavità superiore e inferiore, la cui energia è data rispettivamente da:
[2] formula
e da
[3] formula.
In particolare, se l'eccitazione elettronica e il fotone di cavità sono esattamente risonanti (Ec=Ee), il loro accoppiamento forte dà luogo a un doppietto di nuovi stati, energeticamente separati tra loro della quantità E+−E−=ℏℏℏΩ (separazione di Rabi). Il regime di accoppiamento forte, inizialmente studiato in microcavità planari, è stato recentemente osservato con separazioni di Rabi dell'ordine delle centinaia di μeV anche in sistemi a scatola analoghi a quelli in cui si osserva, in regime di accoppiamento debole, l'effetto Purcell. Oltre a ridurre le larghezze di riga in gioco, per raggiungere il regime di accoppiamento forte è necessario ottenere una frequenza di Rabi elevata aumentando la forza dell'interazione luce-materia, ovvero la forza di oscillatore della transizione elettronica.
Polaritoni eccitonici di microcavità
Nei dispositivi con microcavità planari quali VCSEL e MC-LED il mezzo attivo ha una banda di emissione relativamente ampia dovuta alla ricombinazione di elettroni e buche. In questo caso, anche in presenza di un elevato fattore di qualità della cavità, i rapidi processi di defasamento nel plasma di elettroni e buche impediscono il raggiungimento del regime di accoppiamento forte. Tuttavia, nei semiconduttori, oltre alla banda di emissione per ricombinazione di elettroni e buche non correlati, si osserva il decadimento radiativo di coppie legate elettrone-buca, dette eccitoni. Gli eccitoni in un semiconduttore inorganico (eccitoni di Wannier) hanno una struttura analoga a quella dell'atomo di idrogeno, essendo buca ed elettrone legati dalla mutua attrazione coulombiana come protone ed elettrone, ma con una energia di legame molto più piccola (dell'ordine di 10 meV) e un raggio di Bohr molto più grande (dell'ordine di 100 Å). In una microcavità planare in cui il mezzo attivo sia costituito da un pozzo quantico, un eccitone è libero di muoversi come una particella di massa M (data dalla somma delle masse effettive di buca ed elettrone che dipendono dalla struttura a bande del semiconduttore) e la sua legge di dispersione è quindi data da Eec(k∣∣)=Eec(0)+(ℏ2k∣∣2/2M), dove Eec(0) è dell'ordine della gap di energia del semiconduttore, con correzioni dovute all'energia di confinamento del pozzo quantico e all'energia di legame dell'eccitone. Un eccitone di vettore d'onda bidimensionale k∣∣ ed energia Eec(k∣∣) può accoppiarsi solo a un fotone di uguale energia e vettore d'onda bidimensionale, in quanto tali grandezze sono conservate quando l'eccitone decade e il fotone viene emesso, ovvero nel processo opposto in cui il fotone viene assorbito e l'eccitone creato. L'efficacia di tali processi dipende dalla forza d'oscillatore dell'eccitone che ne determina l'interazione con la luce. Poiché la forza d'oscillatore di un eccitone in un pozzo quantico può avere valori elevati e la sua larghezza di riga può essere sufficientemente ridotta ‒ in particolare alle basse temperature e in strutture di elevata qualità cristallina ‒, è stato possibile raggiungere in una microcavità planare il regime di accoppiamento forte tra eccitoni e fotoni di cavità con la formazione dei polaritoni eccitonici di cavità.
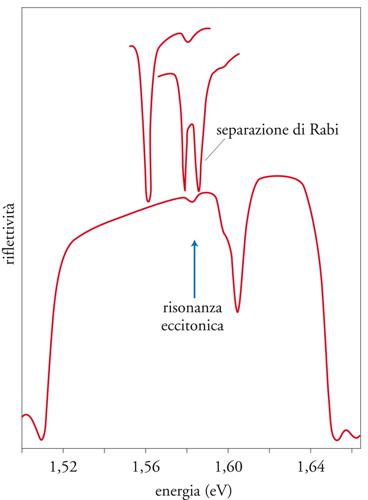
Ciò è di grande interesse, in quanto ha consentito, a partire dai primi anni Novanta, lo studio dell'elettrodinamica quantistica di cavità in sistemi a stato solido con potenziali ricadute tecnologiche. Infatti, a differenza dei polaritoni eccitonici che si formano all'interno di un cristallo non confinato dal mescolamento di un eccitone e di un fotone e che hanno lo stesso vettore d'onda tridimensionale, i polaritoni eccitonici bidimensionali di cavità sono direttamente accessibili tramite gli specchi la cui riflettività non è totale e possono essere osservati facilmente con le usuali tecniche spettroscopiche (misure di riflettività, trasmissione e fotoluminescenza). In particolare, in regime di accoppiamento forte, quando il modo di cavità è risonante con l'eccitone del pozzo quantico, si osservano due minimi nella riflettività della cavità, corrispondenti ai polaritoni superiore e inferiore la cui differenza di energia è ℏℏΩ, invece che un solo minimo come avviene in regime di accoppiamento debole (fig. 3). Inoltre, variando l'angolo di incidenza e quindi il vettore d'onda k∣∣, si può misurare direttamente la legge di dispersione dei polaritoni bidimensionali di cavità, data da
[4] formula
e da
[5] formula
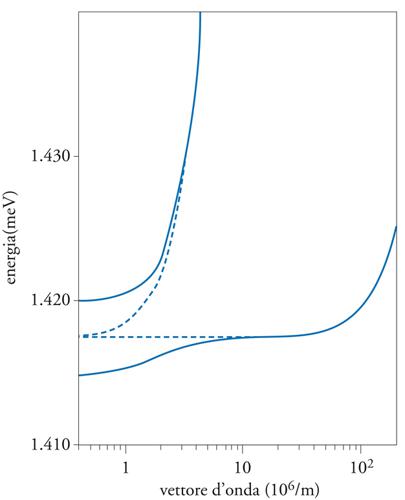
dove Efc(k∣∣) e Eec(k∣∣) sono, rispettivamente, la dispersione dei fotoni di cavità e degli eccitoni del pozzo quantico, mentre la frequenza di Rabi è in prima approssimazione indipendente dal vettore d'onda (fig. 4).
Le leggi di dispersione dei polaritoni di cavità possono essere controllate variando i parametri del sistema, in particolare lo spessore della cavità che ne determina la frequenza di risonanza e il suo fattore di qualità, come pure la natura e il numero dei pozzi quantici da cui dipendono l'energia e la forza d'oscillatore della transizione elettronica attiva.
La differenza di energia Efc(k∣∣=0)−Eec(k∣∣=0), detta detuning della cavità, è tipicamente confrontabile con ℏℏΩ ed è uno dei parametri più significativi del sistema. Uno stato polaritonico è costituito da una sovrapposizione di eccitone e fotone il cui peso relativo varia a seconda del detuning e del vettore d'onda, la composizione divenendo paritetica quando eccitone e fotone abbiano esattamente la stessa energia in assenza del mutuo accoppiamento. Tale condizione, quando il detuning della cavità è negativo, si può ottenere all'aumentare di k∣∣ in quanto l'energia del fotone di cavità cresce molto più rapidamente di quella dell'eccitone. Le curve di dispersione del fotone di cavità e dell'eccitone, che in assenza di accoppiamento luce-materia si incrocerebbero, in regime di accoppiamento forte non coincidono mai, e la differenza minima di energia tra di loro (detta punto di anticrossing) è proprio data dalla separazione di Rabi. In microcavità basate sui semiconduttori inorganici tradizionali, le separazioni di Rabi tipicamente ottenibili sono dell'ordine di 10 meV. Valori molto più elevati ‒ fino alle centinaia di meV ‒, sono stati ottenuti in microcavità contenenti materiali organici i cui eccitoni molecolari (eccitoni di Frenkel) hanno una forza di oscillatore molto maggiore di quella degli eccitoni di Wannier. Valori elevati della separazione di Rabi sono, in particolare, necessari per ottenere il regime di accoppiamento forte a temperatura ambiente. Possibilità di ulteriori sviluppi sono offerte da strutture ibride organico-inorganiche in cui eccitoni di Frenkel, eccitoni di Wannier e fotoni di cavità sono completamente mescolati, dando luogo a polaritoni eccitonici ibridi bidimensionali.
Condensati quantistici in microcavità
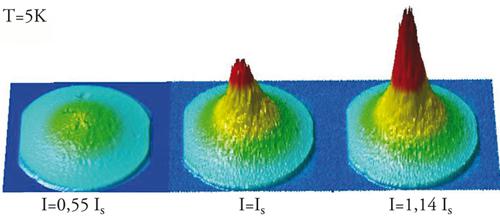
Uno degli aspetti più significativi della dispersione dei polaritoni di cavità è costituito dal fatto che il polaritone inferiore presenta al variare del vettore d'onda bidimensionale un minimo di energia molto pronunciato a piccoli valori di k∣∣. Questa regione di vettori d'onda presenta altresì una piccola densità degli stati e ben si presta al raggiungimento di numeri di occupazione elevati per i quali il carattere bosonico degli stati polaritonici gioca un ruolo essenziale. In particolare, quando tali stati al fondo della banda del polaritone inferiore iniziano a essere occupati, l'ulteriore accumulo dei polaritoni che si ha in essi è favorito dal fattore di stimolazione bosonico, tanto da indurre il raggiungimento di elevati numeri di occupazione sia in opportune condizioni di pompaggio ottico (amplificazione parametrica), sia per rilassamento da stati eccitati incoerenti. In quest'ultimo caso, si è ottenuta evidenza, molto recentemente, della formazione spontanea di un condensato di Bose-Einstein dei polaritoni di cavità (fig. 5). Dal punto di vista della ricerca di base, quindi, si è aperta la possibilità di studiare un nuovo stato quantistico macroscopicamente coerente in un sistema a stato solido. Anche se è ancora presto per prevedere applicazioni tecnologiche di tali risultati scientifici, si può senz'altro menzionare la possibilità di realizzare laser a polaritoni, in cui luce monocromatica coerente viene emessa per emissione spontanea dai polaritoni condensati.
Bibliografia
Agranovich, Bassani 2003: Electronic excitations in organic based nanostructures, edited by Vladimir M. Agranovich, Franco Bassani, Amsterdam, Academic Press, 2003.
Burstein, Weisbuch 1995: Confined electrons and photons, edited by Elias Burstein, Claude Weisbuch, New York, Plenum, 1995.
Ciuti 2003: Ciuti, Cristiano - Schwendimann, Paolo - Quattropani, Antonio, Theory of polariton parametric interactions in semiconductor microcavities, "Semiconductor science and technology", 18, 2003, pp. S279-S293.
Gérard 1998: Gérard, Jean-Michel e altri, Enhanced spontaneous emission by quantum boxes in a monolithic optical microcavity, "Physical review letters", 81, 1998, pp. 1110-1113.
Iga 2000: Iga, Kenichi, Surface-emitting laser. Its birth and generation of new optoelectronics field, "IEEE journal of selected topics in quantum electronics", 6, 2000, pp. 1201-1215.
Kasprzak 2006: Kasprzak, Jacek e altri, Bose-Einstein condensation of exciton polaritons, "Nature", 442, 2006, pp. 409-414.
Kavokin, Malpuech 2003: Kavokin, Alexey - Malpuech, Guillaume, Cavity polaritons: thin films and nanostructures, San Diego, Elsevier, 2003.
Lidzey 1998: Lidzey, David G. e altri, Strong exciton-photon coupling in an organic semiconductor microcavity, "Nature", 395, 1998, pp. 53-55.
Reithmaier 2004: Reithmaier, Johann Peter e altri, Strong coupling in a single quantum dot-semiconductor microcavity system, "Nature", 432, 2004, pp. 197-200.
Savona 1995: Savona, Vincenzo e altri, Quantum well excitons in semiconductor microcavities: unified treatment of weak and strong coupling regimes, "Solid state communications", 93, 1995, pp. 733-739.
Skolnick 1998: Skolnick, Maurice S. - Fisher, T.A. - Whittaker, David M., Strong coupling phenomena in quantum microcavity structures, "Semiconductor science and technology", 13, 1998, pp. 645-669.
Weisbuch 1992: Weisbuch, Claude e altri, Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity, "Physical review letters", 69, 1992, pp. 3314-3317.
Yamamoto, Slusher 1993: Yamamoto, Yoshihisa - Slusher, Richard E., Optical processes in microcavities, "Physics today", 46, 1993, pp. 66-74.
Yokoyama, Ujihara 1995: Spontaneous emission and laser oscillation in microcavities, edited by Hiroyuki Yokoyama, Kikuo Ujihara, Boca Raton-London, CRC Press, 1995.