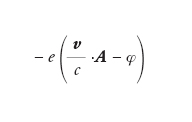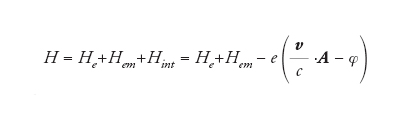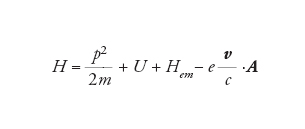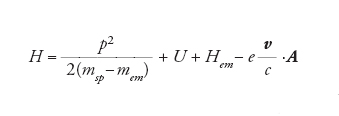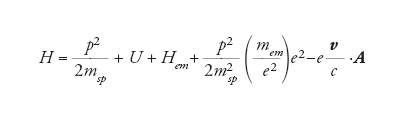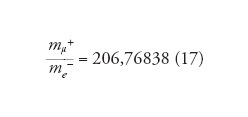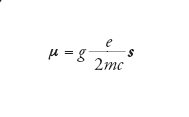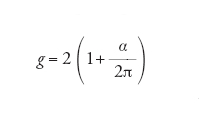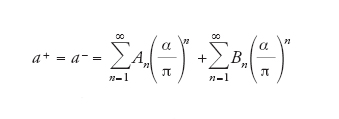Elettrodinamica quantistica: verifiche sperimentali

Elettrodinamica quantistica: verifiche sperimentali

L'elettrodinamica quantistica (QED, Quantum electrodynamics) è una teoria che descrive, in eccellente accordo con i dati sperimentali, l'interazione tra elettroni, positroni e fotoni. Il procedimento generale per la quantizzazione di un sistema classico consiste nel determinare, per mezzo della funzione lagrangiana, i momenti coniugati alle coordinate del sistema e la funzione hamiltoniana, verificando che per questa via si ottengano le corrette equazioni classiche del moto, che successivamente sono trasformate nelle corrispondenti equazioni quantistiche sostituendo alle parentesi di Poisson le parentesi di commutazione. Tale procedimento può essere applicato a un campo d'onda ψ(r, t), che è dotato evidentemente di un numero infinito di gradi di libertà e che, così come un sistema di un numero infinito di particelle è specificato dalle coordinate di posizione e dalla loro dipendenza dal tempo, è individuato dalla propria ampiezza in tutti i punti dello spazio in funzione del tempo. Risulta quindi naturale usare le ampiezze ψ(r, t) come coordinate, analoghe alle coordinate q_i(t) delle particelle. È possibile, tuttavia, procedere diversamente, sviluppando ψ in serie di un insieme completo ortonormale di funzioni u_k:

ψ(r, t)=Sa_k(t)u_k(r)

dove il simbolo S indica un integrale oppure una somma. I coefficienti dello sviluppo nella [1] possono essere considerati come le coordinate del campo, e le equazioni del campo possono essere espresse per mezzo della ψ oppure delle a_k. Questa tecnica di quantizzazione si applica anche al campo elettromagnetico.

Le equazioni dell'elettrodinamica quantistica erano già note alla fine degli anni Venti del Novecento e la teoria era contenuta nei lavori classici di Paul A.M. Dirac, Werner Heisenberg, Wolfgang Pauli ed Enrico Fermi. Il metodo consisteva nello sviluppare in serie di potenze della costante di struttura fine α=e²/ℏc≃1/137 le funzioni d'onda che rappresentano le grandezze fisiche in esame (e è la carica dell'elettrone, ℏ=h/2π è la costante di Planck divisa per 2π e c è la velocità della luce nel vuoto). L'applicazione del metodo perturbativo all'elettrodinamica forniva però risultati divergenti, e perciò non soddisfacenti, che si cercò di migliorare introducendo fattori di forma di vario tipo che permettessero di eliminare le divergenze prive di corrispondenza con i dati sperimentali, secondo una tecnica che però non diede i risultati sperati e che fu perciò abbandonata. In ogni caso, al primo ordine dello sviluppo si ottenevano risultati corretti e perciò le equazioni di base della teoria sembravano giuste. Occorreva trovare il modo di evitare le espressioni divergenti dovute alle correzioni radiative, introdotte nella teoria perturbativa dai termini di ordine superiore al primo, e tale obiettivo fu raggiunto mediante la teoria della rinormalizzazione.

L'era moderna dell'elettrodinamica quantistica

L'era moderna dell'elettrodinamica quantistica iniziò nella seconda metà degli anni Quaranta del XX sec. con le misurazioni del momento magnetico dell'elettrone e del Lamb shift, che diedero impulso allo sviluppo della teoria fino al raggiungimento, grazie soprattutto ai contributi di Hans Bethe, Sin-Itiro Tomonaga, Julian Schwinger, Richard Feynman e Freeman Dyson, della sua formulazione attuale: la regolarizzazione della teoria fu ottenuta mediante la tecnica della rinormalizzazione. Per illustrare il ragionamento che sottende a tale tecnica, è necessario addentrarsi un po' nel formalismo. Se consideriamo un sistema costituito da un campo elettromagnetico in presenza di un elettrone, l'operatore hamiltoniano si può scrivere come la somma di tre termini: il primo, H_e, si riferisce all'elettrone isolato, ed è quello che si avrebbe se il campo elettromagnetico non ci fosse; il secondo, H_em, è relativo al solo campo elettromagnetico, come se l'elettrone non ci fosse; vi è infine un termine di interazione H_int, la cui forma è:

[2]  formula

in cui v è la velocità dell'elettrone e A e φ sono i potenziali vettore e scalare del campo elettromagnetico nella posizione occupata dall'elettrone. L'hamiltoniano totale del sistema è quindi:

[3] formula.

Il problema fondamentale della dinamica del sistema è quello di risolvere l'equazione di Schrödinger il cui operatore hamiltoniano sia dato dalla [3]. Consideriamo il caso non relativistico, in cui l'elettrone si muova con piccole velocità rispetto alla velocità della luce. L'approssimazione che si utilizza nel risolvere l'equazione di Schrödinger consiste nel considerare H_e+H_em come la parte imperturbata del sistema e H_int come la perturbazione. Il sistema non perturbato è abbastanza semplice da trattare, poiché il campo elettromagnetico non è influenzato dall'elettrone, e viceversa. Il termine H_e rappresenta l'energia dell'elettrone, somma dell'energia cinetica p²/2m ‒ nel caso non relativistico, essendo p la quantità di moto ‒ e dell'energia potenziale U. L'hamiltoniano H_em è l'energia del campo elettromagnetico, che, come si può dimostrare, vale:

[4] H_em= ℏc ∑ω_kN_λ(k)

dove ω_k=∣k∣ e N_λ(k)=a_λ^†(k)a_λ(k). L'indice λ fornisce la polarizzazione del campo elettromagnetico e k è il momento degli oscillatori mediante i quali si rappresenta la radiazione. L'energia del sistema si può scrivere, nel caso φ=0:

[5] formula.

Se si studia lo spostamento dei livelli energetici dello spettro dell'atomo di idrogeno mediante il ricorso alla teoria delle perturbazioni, il risultato che si ottiene dalla [5] è nullo al primo ordine e diverge al secondo ordine. Questo significa che il primo termine dello sviluppo, proporzionale a e, ha un coefficiente nullo, mentre il secondo termine, proporzionale a e², ha un coefficiente infinito. Il risultato sperimentale ottenuto dalla misurazione dello spettro di struttura fine dell'idrogeno non poteva essere, quindi, in accordo con il calcolo perturbativo. L'idea discussa da Bethe fu quella di chiedersi quale fosse il valore della massa m da usare nell'espressione p²/2m. L'ipotesi di scrivere l'hamiltoniano come somma di tre termini si fonda sulla possibilità di separare tra loro i contributi relativi rispettivamente al solo elettrone, al solo campo elettromagnetico e al termine di interazione. La quantità p²/2m deve riferirsi perciò al solo elettrone, del quale m è la massa meccanica, ossia il valore della massa dell'elettrone quando non è in presenza del campo elettromagnetico. Quando, nel condurre i calcoli, si sostituisce a m il valore sperimentale m_sp=m+m_em si compie un'operazione non corretta. La [5] va piuttosto scritta:

[6] formula.

La massa elettromagnetica è un effetto del secondo ordine, che si manifesta quando il campo di radiazione interagisce con l'elettrone, ed è quindi proporzionale a e²:

[7] formula.

La [7] mette bene in evidenza l'esistenza di due perturbazioni, di cui una, e(v/c)∙A, dà un risultato nullo al primo ordine e un risultato infinito al secondo ordine e l'altra, p²/2m_sp²(m_em/e²)e², dà anch'essa un risultato infinito ma di segno contrario al precedente. Il punto essenziale dell'osservazione di Berthe è che le due parti infinite si cancellano e rimane un risultato finito, che, nel caso della struttura fine dell'atomo d'idrogeno, è molto vicino a quello sperimentale. La teoria di Bethe, ricorrendo a un calcolo non relativistico, non è invariante per trasformazioni di Lorentz e fornisce risultati non corretti per valori dell'energia dell'ordine di m_spc². I successivi lavori di Tomonaga, Schwinger, Feynman e Dyson hanno sviluppato uno schema teorico estremamente elegante, che ha esteso l'idea di Bethe al caso relativistico e ha permesso di interpretare e predire con successo i fenomeni fisici dell'elettrodinamica alle alte energie.

L'estensione della teoria della rinormalizzazione al regime di moto relativistico ha costituito un arduo problema matematico. Tale estensione prevede l'introduzione di operatori di campo, che rappresentano le operazioni di distruzione e di creazione di un fotone, di un elettrone e di un positrone. In conformità ai principî generali della teoria dei campi quantistici, lo stato di un sistema è descritto da un funzionale che dipende dal numero di elettroni, positroni e fotoni, dalla loro energia, dalla loro quantità di moto e dal momento della quantità di moto intrinseco, lo spin. In elettrodinamica quantistica è definito uno stato di vuoto: se a esso si applicano operatori di creazione, si generano nuovi stati contenenti un qualsiasi numero assegnato di elettroni, positroni e fotoni, con valori di energia-impulso ed elicità definiti a priori. Il vuoto è lo stato del sistema che possiede il valore minimo del quadrivettore energia-quantità di moto ed è invariante per trasformazioni di Lorentz, vale a dire che, se si cambia il sistema di riferimento, il sistema permane in uno stato vuoto. La teoria dei campi, e in particolare la QED, insegna che il vuoto è simile a un sistema dinamico di spin nullo, il cui quadrivettore energia-quantità di moto tende ad avere anch'esso un valore nullo. Come un campo di spin nullo, al vuoto possono essere assegnati numeri quantici quali lo spin isotopico, la parità, la stranezza e così via.

Interpretazione grafica di alcuni processi di elettrodinamica

Scopo dell'elettrodinamica è quello di calcolare la probabilità che una configurazione fisica iniziale evolva in una configurazione finale assegnata. La teoria permette di costruire un operatore unitario, la matrice S, la cui forma esplicita è estremamente complessa ma i cui termini forniscono la probabilità che uno stato iniziale evolva in un dato stato finale. I vari termini della serie perturbativa possono essere rappresentati graficamente in modo molto suggestivo, come suggerito da Feynman. L'n-esimo termine della serie perturbativa descrive n interazioni successive tra il campo elettromagnetico, che soddisfa le equazioni di Maxwell, e quello dell'elettrone, che soddisfa l'equazione di Dirac. Ogni interazione è rappresentata graficamente mediante un vertice, al quale sono applicati i seguenti operatori: (a) la creazione o la distruzione di un fotone; (b) la creazione di un elettrone o l'annichilazione di un positrone; (c) la creazione di un positrone o la distruzione di un elettrone. Per ciascun diagramma è necessario poi calcolare l'elemento di matrice dell'operatore S corrispondente.

fig. 2

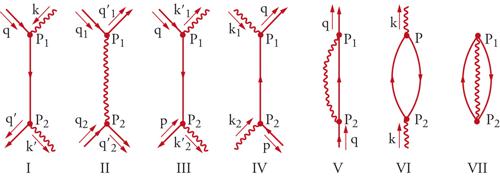
La fig. 2 rappresenta i termini del secondo ordine (n=2) della serie perturbativa della matrice S. Il primo diagramma (I) descrive l'interazione tra un elettrone e un fotone, cioè l'effetto Compton. Le linee ondulate rappresentano un fotone, le linee continue gli elettroni e i positroni. Il simbolo k indica il quadrivettore energia-quantità di moto del fotone, mentre q e p sono i quadrivettori energia-quantità di moto rispettivamente dell'elettrone e del positrone; le frecce associate indicano creazione se puntano lontano dal vertice, distruzione se dirette verso il vertice. I tratti che uniscono i due vertici rappresentano particelle virtuali, ossia particelle che, pur fornendo un'utile schematizzazione dell'operatore S e contribuendo al risultato del calcolo, sono prive di una realtà fisica ben definita e non sono osservabili.

Il secondo diagramma (II) rappresenta l'interazione elettrone-elettrone; il terzo (III) la produzione di coppie di fotoni a causa dell'annichilazione di una coppia elettrone-positrone; il quarto (IV) la produzione di una coppia elettrone-positrone attraverso l'interazione fotone-fotone; il quinto (V) il processo di interazione di un elettrone (o di un positrone) con il campo di radiazione originato dalla carica stessa, ossia l'interazione di un elettrone con il proprio campo di radiazione. Il sesto diagramma (VI) descrive la creazione e la distruzione di una coppia virtuale di elettroni e positroni da parte di un fotone. L'ultimo diagramma (VII) rappresenta la creazione e la successiva distruzione di una coppia virtuale di elettroni e positroni da parte di un fotone anch'esso in uno stato virtuale, ossia in uno stato in cui la quantità di moto, l'energia e la massa del fotone (m_γ=0) non soddisfano le ben note relazioni della relatività. I diagrammi (VI) e (VII) descrivono processi che coinvolgono una coppia virtuale elettrone-positrone; il processo del diagramma (VII) ha luogo nel vuoto, il che implica che coppie virtuali di elettroni e positroni permettono che il vuoto si polarizzi.

I diagrammi (V), (VI) e (VII) sono responsabili delle ben note divergenze in elettrodinamica quantistica. L'eliminazione di tali divergenze si ottiene con la rinormalizzazione della massa m e della carica e dei quanti del campo di Dirac. La procedura in ciascuno dei due casi consiste nell'effettuare una sottrazione tra due quantità infinite e nell'imporre che tale differenza sia uguale, rispettivamente, al valore della massa e della carica elettrica determinato sperimentalmente. La nube di fotoni virtuali (V) aumenta l'energia di un elettrone e ciò si può interpretare, secondo la relatività, come un aumento della massa, dal valore m proprio dell'elettrone libero al valore sperimentale m_sp. La massa sperimentale è quindi m_sp=m+m_em, somma della massa m di un elettrone fittizio e della massa m_em che rappresenta l'azione della nube di fotoni associata al campo elettromagnetico originato dalla carica stessa dell'elettrone. Perché risultino soppresse le divergenze provenienti da m_em, si attribuisce il valore −∞ alla massa m dell'elettrone fittizio e si assegna a m_sp il valore sperimentale.

Una procedura analoga si applica ai diagrammi (VI) e (VII), responsabili della comparsa di divergenze per la carica elettrica. Sia e la carica elettrica di un elettrone libero (quindi fittizio) e sia e₁ una correzione dovuta agli effetti virtuali rappresentati dai diagrammi (VI) e (VII). Alle cariche e ed e₁ si attribuiscono valori infiniti di segno opposto e si impone che la loro somma sia uguale alla carica sperimentale dell'elettrone, cioè e+e₁=e_sp. Una conseguenza importante della teoria della rinormalizzazione è che una particella carica può emettere e assorbire fotoni anche in assenza di un campo elettromagnetico esterno, dando così origine alle cosiddette fluttuazioni del vuoto. Esse hanno importanti conseguenze sperimentali, tra cui l'emissione spontanea della radiazione da parte di un atomo eccitato, lo spostamento dei livelli energetici dell'atomo d'idrogeno (Lamb shift) e l'esistenza di correzioni radiative per il momento magnetico dell'elettrone e del muone.

Verifiche sperimentali dell'elettrodinamica quantistica

La formulazione attuale della teoria dell'elettrodinamica quantistica non è definitiva, poiché le divergenze a cui dà luogo si eliminano ricorrendo a un procedimento ad hoc nella teoria della rinormalizzazione, ed è importante perciò verificare le predizioni della teoria. Le precisioni raggiunte in tali esperimenti sono tra le più alte ottenute in fisica. Le quantità misurate, quali le masse, la costante di struttura fine, la struttura iperfine degli atomi, i momenti magnetici, sono espresse in funzione di costanti fondamentali, in modo da costruire con queste ultime un intreccio di correlazioni. Le verifiche condotte in laboratorio si possono dividere in due classi: esperimenti molto precisi e di bassa energia, che riguardano la fisica atomica e la misurazione dei momenti magnetici dei leptoni e che permettono di confrontare i risultati sperimentali con le previsioni teoriche, verificando le correzioni radiative di ordine superiore al primo e la tecnica della rinormalizzazione. Vi sono inoltre esperimenti di alta energia, che, indagando distanze dell'ordine di 10⁻¹⁸ m e mettendo alla prova le previsioni della QED in situazioni in cui la quantità di moto trasferita durante l'interazione tra leptoni (elettroni o muoni) è la più grande possibile, mostrano come le equazioni di Maxwell, quantizzate mediante correnti di Dirac di elettroni e muoni, siano verificate con una precisione di oltre una parte su mille.

Il Lamb shift del muone

fig. 3

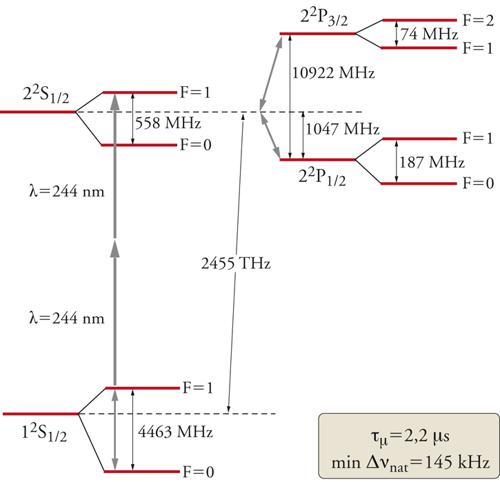
Il muonio è un 'atomo' in cui un elettrone è legato a un muone di carica elettrica positiva. Si tratta di un sistema simile all'atomo di idrogeno, in cui il protone è sostituito da un muone positivo. Possiede caratteristiche ideali per condurre verifiche sulle previsioni dell'elettrodinamica quantistica, in quanto il muone, come l'elettrone, non presenta alcuna struttura interna, laddove la struttura del protone rende impossibile spiegare gli esperimenti in termini della sola QED. Nell'interpretare la struttura iperfine del livello fondamentale dell'atomo di idrogeno, per esempio, vi è un'incertezza di una parte su un milione, sebbene la precisione della relativa misura sia maggiore per sei ordini di grandezza: ciò è dovuto alla minore precisione nella misurazione della polarizzazione del protone e del suo momento magnetico. L'interazione del muonio, invece, è di natura esclusivamente elettromagnetica, cosicché i livelli di energia possono essere calcolati mediante la sola QED, tenendo comunque conto dei contributi che provengono dal bosone intermedio neutro Z⁰ e dall'interazione forte che polarizza il vuoto. Nella fig. 3 sono rappresentati i livelli di energia del muonio negli stati n=1 e n=2. Il muonio può formarsi nello stato fondamentale 1S e le transizioni da uno stato a un altro sono indotte mediante le microonde oppure i laser. A titolo di esempio, riportiamo il valore sperimentale della frequenza di transizione 1S-2S:

[8] Δν_1S−2S (sp) = 2 455 528 941,0 (9,8) MHz

da confrontarsi con il valore teorico:

[9] Δν_1S−2S (sp) = 2 455 528 935,4 (1,4) MHz.

Da questi valori si deduce il rapporto tra la massa del muone positivo e dell'elettrone:

[10] formula.

I momenti magnetici dell'elettrone e del muone

Il rapporto giromagnetico g dell'elettrone (o del muone) è definito dalla seguente relazione:

[11] formula

dove μ è il momento magnetico di dipolo, e è la carica elettrica, m è la massa e s è lo spin, o momento della quantità di moto intrinseco, del leptone (elettrone o muone). Il numero adimensionale g rappresenta una proprietà fondamentale della particella e delle sue interazioni. Nel caso di una sfera carica in rotazione, la meccanica classica prevede g=1. Dal punto di vista quantistico, l'equazione [11] stabilisce una relazione tra gli operatori μ e s, e g misura la deviazione del momento magnetico della particella dal valore determinato classicamente. Il valore sperimentale g del protone è 5,586, mentre per l'elettrone e il muone si ha g=2,002. Sebbene il rapporto giromagnetico g del protone non possa essere calcolato nell'ambito della QED, poiché vi è in tal caso il contributo delle correnti cariche dei quark che costituiscono la complessa struttura del nucleone, quello dell'elettrone e del muone può essere calcolato con precisione, come conseguenza del fatto che i leptoni carichi sono dotati di una struttura semplice. In altre parole, per il protone il rapporto giromagnetico riflette la dinamica interna, descritta mediante la cromodinamica, mentre per i leptoni è il risultato dell'interazione tra la carica elettrica e il campo di radiazione.

La teoria quantistica di Dirac predice per l'elettrone (e il muone) il valore g=2. All'inizio del 1947, John Nafe, Edward Nelson e Isidor Rabi condussero accurate misurazioni della struttura iperfine di idrogeno e di deuterio, che si rivelarono tuttavia in disaccordo con la teoria. Gregory Breit suggerì allora che la discrepanza tra i risultati sperimentali e i calcoli sarebbe scomparsa se si fosse ammesso un valore di g che differiva da 2 (g≠2) per circa l'1 ‰. Schwinger calcolò che la deviazione dal valore g=2 era dovuta a una correzione radiativa del primo ordine in α, vale a dire all'emissione di un fotone virtuale e all'assorbimento dello stesso da parte dell'elettrone che interagisce con il campo magnetico esterno. Il risultato di Schwinger è:

[12] formula.

Il valore misurato da Polykarp Kusch e Henry Foley nel dicembre del 1947 era in accordo con il calcolo di Schwinger. Il risultato sperimentale è:

[13] g = 2(1+ 0,00119(5)).

con un errore di 25 ppm.

Considerazioni teoriche

Il momento magnetico dell'elettrone (o del muone) si può scrivere, tenendo conto che g è lievemente diverso da 2, come

[14] μ = − 2(1+a)μ₀ s

dove a=(g−2)/2 indica la cosiddetta anomalia del momento magnetico. In elettrodinamica quantistica l'anomalia è espressa in serie di potenze della costante di struttura fine:

[15] formula.

I segni + e − indicano che l'anomalia si riferisce rispettivamente a positroni ed elettroni (oppure a muoni positivi e negativi); il teorema CPT (dove C indica l'operatore coniugazione di carica, P la parità e T l'operatore inversione temporale) prevede che le due anomalie coincidano. I coefficienti A_n non dipendono dalla massa del leptone, mentre quelli B_n vi dipendono.

L'anomalia dell'elettrone

Il valore teorico dell'anomalia del momento magnetico dell'elettrone è:

[16] a_e (teo)= 1 159 652 140 (5,3)(4,1)(27,1)∙10⁻¹².

Per calcolare a_e si è fatto uso della costante α, misurata per il tramite dell'effetto Hall. Nella [16] il primo e il secondo numero in parentesi indicano l'incertezza rispettivamente nel calcolo dei termini A₃ e A₄, il terzo numero indica l'incertezza che proviene dall'errore della misura di α. Il calcolo dell'anomalia è al quarto ordine in α e il risultato teorico è in accordo (entro 1,7 deviazioni standard) con la misura sperimentale, che è:

[17] a_e− = 1 159 652 188,4 (4,3)∙10⁻¹².

[18] a_e+ = 1 159 652 187,9 (4,3)∙10⁻¹².

Il confronto tra la [17] e la [18] permette una valida verifica del teorema CPT. I contributi alla polarizzazione del vuoto dovuti alla coppia muone-antimuone, agli adroni e alle interazioni elettrodeboli sono di un ordine di grandezza inferiore rispetto al livello di incertezza della [16].

Le misurazioni di a_e± sono state effettuate ricorrendo a due metodi differenti; in entrambi l'elettrone è sottoposto all'azione di un campo magnetico statico, che interagisce con il momento magnetico dell'elettrone. In un caso si misura la precessione del momento magnetico rispetto al momento della quantità di moto, nell'altro si induce una transizione tra due livelli energetici dell'elettrone sottoposto al campo magnetico. Un risultato preliminare riportato da Brian Odom nella propria tesi di dottorato all'Università di Harvard nell'ottobre 2004 è:

[19] a_e− = 1 159 652 180 8,6(5,7)∙10⁻¹³ (0,5 ppb).

Questo risultato tiene conto non solamente delle interazioni tra elettroni e fotoni, ma anche dei contributi che sono apportati alla polarizzazione del vuoto da coppie virtuali di muoni positivi e negativi e da adroni. Il contributo delle coppie virtuali di muoni-antimuoni è pari a a_e=27,21∙10⁻¹³, quello delle coppie di adroni è a_e=16,42∙10⁻¹³, con una incertezza (27)∙10⁻¹³. Per un confronto tra la teoria e i risultati sperimentali si rende necessaria una misurazione più precisa della costante di struttura fine α.

Il momento magnetico anomalo del muone

Le correzioni radiative comportano che anche il rapporto giromagnetico del muone sia diverso dal valore 2 previsto dalla teoria di Dirac. Tre esperimenti di precisione progressivamente crescente sono stati realizzati presso il CERN (Centro Europeo per la Ricerca Nucleare) di Ginevra. A distanza di circa vent'anni dall'ultimo dei tre (durato dal 1971 al 1978), un nuovo esperimento è stato condotto allo AGS (Alternating Gradient Synchrotron) di Brookhaven, negli Stati Uniti, sfruttando lo stesso principio ma ricorrendo a una tecnologia più aggiornata e migliorando di almeno un fattore 10 la precisione rispetto al CERN. La misurazione del momento magnetico anomalo del muone è importante perché permette di verificare se la QED predica il corretto valore dell'anomalia al secondo ordine nello sviluppo perturbativo in α e consente di valutare i contributi al momento magnetico del muone provenienti dalla teoria elettrodebole e dalle interazioni tra adroni. Il terzo degli esperimenti effettuati al CERN ha evidenziato il contributo delle interazioni forti alla polarizzazione del vuoto, mentre con la sensibilità raggiunta nell'esperimento di Brookhaven si possono evidenziare le correzioni virtuali dovute all'interazione debole. Il valore teorico del rapporto giromagnetico del muone previsto dalla QED, tenuto anche conto delle correzioni dovute alle interazioni deboli e adroniche, è in accordo entro 2,7 deviazioni standard con quello sperimentale. Le misure dei rapporti giromagnetici del muone e dell'elettrone, insieme a quelle della costante di Rydberg, della velocità della luce e della frequenza del maser di idrogeno, sono tra le più precise in fisica.

Verifiche sperimentali della QED ad alte energie

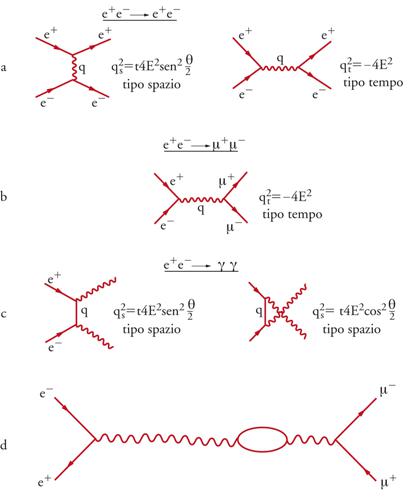
Gli esperimenti condotti negli anelli di collisione (collider) e⁺e⁻ oppure e⁻e⁻ coinvolgono reazioni con alta quantità di moto trasferita. Il capostipite degli anelli di collisione e⁺e⁻ fu AdA, una macchina relativamente modesta ma innovativa, costruita a Frascati nel 1960 su progetto di Bruno Touschek. Il sistema di riferimento privilegiato si rivela quello del centro di massa, in cui il quadrivettore energia-quantità di moto di una particella può contribuire per intero alla creazione di nuovi stati fisici. Gli esperimenti presso gli anelli di collisione (e⁺e⁻) e (e⁻e⁻) hanno verificato le previsioni della QED a distanze dell'ordine di 10⁻¹⁸ m, stabilendo che le equazioni di Maxwell quantizzate e la corrente di Dirac forniscono risultati corretti. Gli anelli di collisione del tipo LEP (Large electron-positron collider) sono strumenti possenti, atti a fornire una notevole statistica per lo studio di nuove particelle. I processi fisici che sono stati studiati alle alte energie sono:

e⁺e⁻ → e⁺e⁻ (diffusione Bahaba)

e⁺e⁻ → μ⁺μ⁻ (produzione di coppie di muoni)

e⁺e⁻ → γγ (annichilazione elettrone-positrone in coppie di fotoni).

fig. 4

Nella fig. 4 sono rappresentati tre diagrammi di Feynman al primo ordine nella costante di struttura fine, che descrivono alcune reazioni misurate con crescente precisione e a energie sempre più elevate; nella figura sono anche indicati i q² di genere spazio e di genere tempo nel centro di massa del sistema. Le sezioni d'urto differenziali misurate sono confrontate con quelle calcolate teoricamente, mediante l'introduzione dei cosiddetti fattori di forma: un'eventuale violazione della QED potrebbe manifestarsi per grandi valori della quantità di moto associata al propagatore del fotone, del muone o dell'elettrone, oppure ai vertici muone-fotone o elettrone-fotone; propagatori e vertici possono essere moltiplicati per fattori di forma che stabiliscono un limite per il quadrimpulso trasferito, in corrispondenza del quale la QED potrebbe perdere validità. Si tratta di un modello dalla valenza eminentemente pratica, che permette di confrontare risultati di differenti esperimenti, ma non va dimenticato che le situazioni fisiche cui si riferiscono sono tra loro ben diverse. I risultati appena descritti si possono esprimere introducendo una lunghezza fondamentale, che descrive la non località delle interazioni tra leptoni e fotoni: l₀≃ℏℏ/Λc≤5∙10⁻¹⁶ cm, dove Λ indica un 'taglio', che dagli esperimenti condotti presso l'elettrosincrotrone Desy in Germania risulta dell'ordine di 500 GeV.

L'elettrodinamica quantistica è una teoria verificata con notevole precisione, che descrive l'interazione della carica elettrica con il campo elettromagnetico ed è il modello di riferimento per la costruzione di moderne teorie di campo. Nonostante i successi riportati, si ritiene che il processo che è alla base della QED costituisca una questione non ancora risolta: la rinormalizzazione appare come una teoria troppo complicata per descrivere un fenomeno fisico fondamentale quale l'interazione tra la carica elettrica e il campo elettromagnetico, e d'altra parte sarebbe opportuno avere una formulazione teorica da cui fossero escluse le divergenze. La possibilità di raggiungere energie sempre più elevate aiuterà, forse, a comprendere sempre meglio l'interazione tra la carica elettrica e il campo elettromagnetico. Gli esperimenti realizzati mediante gli anelli di collisione e⁺e⁻, sia al Single linear collider (SLC) a Stanford (Stati Uniti), sia al LEP e al CERN (Ginevra) hanno raggiunto energie tali da consentire la produzione dei bosoni vettoriali pesanti Z⁰ e W^±, permettendo la verifica del Modello Standard della teoria elettrodebole con una precisione superiore a una parte su diecimila. Il LEP, in particolare, raggiungendo una energia di 200 GeV nel centro di massa per l'interazione e⁺e⁻, ha messo in evidenza i contributi delle correzioni radiative alla produzione dei bosoni vettoriali e ha mostrato come l'elettrodinamica quantistica e la teoria delle interazioni deboli si unifichino nella teoria elettrodebole intorno ai 100 GeV.

Bibliografia

Bethe, Salpeter 1957: Bethe, Hans A. - Salpeter, Edwin E., Quantum mechanics of one- and two-electron atoms, Berlin, Springer, 1957.

Brown, Gabrielse 1986: Brown, Lowell S. - Gabrielse, Gerald, Geonium theory: physics of a single electron or ion in a Penning trap, "Review of modern physics", 58, 1986, pp. 233-311.

Combley, Picasso 1974: Combley, Fred - Picasso, Emilio, The muon (g-2) precession experiments: past, present and future, "Physics reports", 14, 1974, pp. 1-58.

Dirac 1959: Dirac, Paul A.M., I principi della meccanica quantistica, Torino, Boringhieri, 1959 (ed. orig.: The principles of quantum mechanics, Oxford, Clarendon, 1939).

Farley, Picasso 1990: Farley, Francis J.M. - Picasso, Emilio, The muon (g-2) experiments, in: Quantum electrodynamics, edited by Toichiro Kinoshita, Singapore, World Scientific, 1990, pp. 474-553.

Farley, Semertzidis 2004: Farley, Francis J.M. - Semertzidis, Yannis K., The 47 years of muon g-2, "Progress in particle and nuclear physics", 52, 2004, pp. 1-83.

Kinoshita 1990: Kinoshita, Toichiro, Theory of the anomalous magnetic moment of the electron. Numerical approach, in: Quantum electrodynamics, edited by Toichiro Kinoshita, Singapore, World Scientific, 1990, pp. 218-314.

Martyn 1990: Martyn, H.U., Test of QED by high energy electron-positron collisions, in: Quantum electrodynamics, edited by Toichiro Kinoshita, Singapore, World Scientific, 1990, pp 92-156.

Mehra, Rechenberg 1987-2001: Mehra, Jagdish - Rechenberg, Helmut, The historical development of quantum theory, New York, Springer, 1987-2001, 6 v.

Pipkin 1990: Pipkin, Francis M., Lamb shift measurements, in: Quantum electrodynamics, edited by Toichiro Kinoshita, Singapore, World Scientific, 1990, pp. 696-773.

Schiff 1952: Schiff, Leonard I., Meccanica quantistica, Torino, Edizioni Scientifiche Einaudi, 1952, pp. 473-558 (ed. orig.: Quantum mechanics, McGraw-Hill, New York, 1949).

Van Dyck 1990: van Dyck, Robert S. jr, Anomalous magnetic moment of single electrons and positrons: experiment, in: Quantum electrodynamics, edited by Toichiro Kinoshita, Singapore, World Scientific, 1990, pp. 322-382.