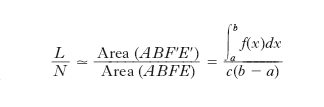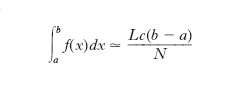montecarlo, metodo
Metodo numerico basato su procedimenti probabilistici, usato in statistica per la risoluzione di problemi di varia natura, che presentano difficoltà analitiche non altrimenti o difficilmente superabili. Prende nome dal casinò di Monte Carlo, simbolo del gioco d’azzardo per antonomasia.
Generalità
Concettualmente il metodo si basa sulla possibilità di eseguire, utilizzando numeri estratti a caso (numeri casuali), un campionamento di una distribuzione di probabilità assegnata, F(X); ossia sulla possibilità di generare una sequenza di eventi X1, X2, ..., Xn, ..., distribuiti secondo la F(X). In pratica, invece di servirsi di un campione di numeri effettivamente estratti a caso, si ricorre a una sequenza di numeri ottenuti con un processo iterativo ben determinato; tali numeri vengono detti pseudo-casuali giacché, pur non essendo casuali, hanno proprietà statistiche analoghe a quelle dei veri numeri casuali. Al metodo m. sono riconducibili molti metodi di simulazione, che mirano alla determinazione dei parametri tipici dei fenomeni complessi a carattere aleatorio.
Una delle caratteristiche principali del metodo è che la soluzione ottenuta non è mai esatta, benché rigorosa in senso statistico. L’incertezza sulla soluzione è tanto minore quanto più grande è il campione statistico (o, in altri termini, l’investimento di tempo di calcolo). La convenienza o meno del metodo m. rispetto a tecniche alternative dipende soprattutto dal rapporto qualità/prezzo; in molti casi, soprattutto nello studio di sistemi (reali o artificiali) ad alta complessità, il metodo m., pur richiedendo un dispendio notevole di risorse, è l’unico in grado di offrire risposte affidabili.
Sviluppo del metodo
Il documento più antico che riferisce dell’uso di tecniche stocastiche per la soluzione di un integrale si può forse far risalire a Buffon, che nel 1777 descriveva l’esperimento seguente: se si getta un ago di lunghezza L su di un piano orizzontale su cui siano tracciate delle linee parallele a distanza d le une dalle altre (con d>L), qual è la probabilità P che l’ago intersechi una di queste linee? Buffon eseguì l’esperimento gettando più volte l’ago per determinare il valore di P. Inoltre dimostrò che la soluzione analitica del problema è P=2L/(πd). Alcuni anni più tardi, P.-S. Laplace suggerì che questo esperimento poteva essere utilizzato per stimare π, il che equivale a una determinazione m. di π, anche se non la più efficiente.
Il nome m. venne usato per la prima volta nel quadro delle ricerche condotte all’interno del progetto Manhattan sul trasporto di neutroni. Queste ricerche erano legate principalmente ai nomi di J.L. von Neumann, S.M. Ulam, N. Metropolis ed E. Fermi. Quest’ultimo aveva già precedentemente condotto alcuni esperimenti numerici (che potremmo oggi definire m.) sul modo in cui particelle neutre interagivano con la materia condensata.
A partire dalla fine degli anni 1940 si osservò un interesse sempre crescente verso le tecniche m., con la comparsa di numerosi articoli scientifici che descrivevano il metodo e le sue applicazioni ai campi del sapere più svariati, dalla meccanica statistica all’economia, dalla fisica nucleare alla matematica applicata. A questo sviluppo contribuirono sia i notevoli progressi nel campo della teoria delle probabilità e dei processi stocastici, sia l’introduzione dei primi elaboratori digitali. Fu comunque solo con l’avvento dei grandi elaboratori veloci (caratterizzati da alte velocità di elaborazione e grande memoria di massa) e con la messa a punto di tecniche di ottimizzazione delle procedure (rivolte alla minimizzazione degli errori statistici) che il metodo m. poté raggiungere i livelli di sviluppo e utilizzo attuali.
Applicazioni
Tra le applicazioni si possono ricordare: la risoluzione di problemi di analisi numerica, quali, per es., il calcolo di integrali definiti, la soluzione di equazioni alle differenze finite, differenziali, algebriche ecc.; lo studio dei sistemi modello, sviluppati nella teoria delle code, per descrivere la formazione e lo smaltimento delle code in sistemi di varia complessità, come le centraline telefoniche, i sistemi di calcolo ad alto parallelismo, gli aeroporti, le autostrade ecc.; la simulazione di fenomeni naturali di tipo stocastico, come il trasporto di carica in materiali semiconduttori e in dispositivi elettronici a semiconduttore, la crescita di cristalli, i fenomeni ottici nell’atmosfera, il trasporto di neutroni in una reazione nucleare ecc. Le tecniche m. sono molto usate anche nella fisica teorica (per studiare, per es., le teorie quantistiche di campo, i fenomeni critici e le transizioni di fase) e, in generale, in ogni campo d’indagine che debba trattare sistemi a molti gradi di libertà.
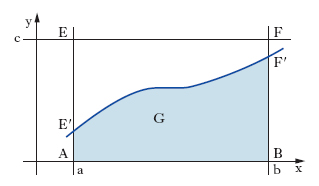
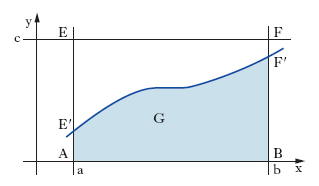
Come esempio di applicazione consideriamo il calcolo dell’integrale definito tra gli estremi a, b, di una funzione f(x) con 0<f(x)≤c. Considerata una coppia di numeri pseudo-casuali (Xi, Yj) indipendenti con a≤Xi≤b e 0<Yj≤c, sia Zi una variabile che assume il valore 1 se f(Xi)<Yj, e 0 altrimenti. Su N coppie di (Xi, Yj) il numero complessivo dei punti che cadono nella regione G indicata in fig. sarà:
Se N è sufficientemente grande, per la legge dei grandi numeri, sarà:
e quindi:
È possibile, poi, determinare la precisione in funzione del numero di coppie N di numeri pseudo-casuali e il numero N in funzione della precisione desiderata.