flesso
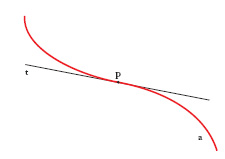
In matematica, si definisce f. ordinario di una curva piana un suo punto d’inflessione, cioè un punto P (v. fig.) nel quale la curva a attraversa la propria tangente t (mentre la curva sta tutta da una stessa banda rispetto alla tangente nelle vicinanze di un punto ordinario).
La tangente t alla curva in un f. ordinario si chiama tangente di f. e ha contatto generalmente tripunto con la curva stessa.
Si hanno poi i f. di ordine superiore quando più intimo è il contatto tra curva e tangente; non sempre, in essi, la curva è attraversata dalla tangente t di flesso. I f. di una curva algebrica piana di ordine n priva di singolarità coincidono con i punti d’intersezione della curva con la sua hessiana, e il loro numero è pertanto 3n(n-2) (➔ Plücker, Julius).
Più in generale, per una curva piana, regolare, di equazioni parametriche x=x(m), y=y(m), condizione necessaria perché un punto sia un f. è che in esso si abbia x′y″−y′x″=0, dove x′, y′, x″, y″ sono i valori delle derivate prime e seconde delle funzioni x(m), y(m), calcolate nel punto in esame. In particolare, se la curva è data dall’equazione cartesiana y=f(x), la condizione diviene: f″=0.