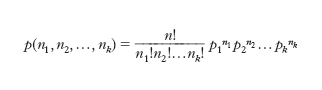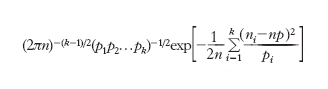multinomiale, distribuzione

Particolare tipo di distribuzione statistica. Precisamente, se da una popolazione, ossia da un insieme di unità con modalità x₁, x₂, ..., x_k e frequenze relative corrispondenti p₁, p₂, ..., p_k, si estrae ‘con ripetizione’ (ossia rimettendo via via nella popolazione le unità estratte) un campione di n unità, la probabilità di osservare n₁ unità della modalità x₁, n₂ unità della modalità x₂, ..., n_k unità della modalità x_k, dove n₁+n₂+... n_k=n è data dalla quantità:

Al variare della variabile k-pla (n₁, n₂, ..., n_k) si ha una distribuzione i cui termini sono dati dallo sviluppo del polinomio (p₁, p₂+...+p_k)ⁿ e che viene detta distribuzione multinominale. Si dimostra che, sotto condizioni poco restrittive, la probabilità p(n₁, n₂, ..., n_k), che male si presta ai calcoli per la presenza dei fattoriali, può essere approssimata soddisfacentemente dalla quantità:

Per k=2, la distribuzione si riduce a quella binomiale e la formula approssimata dà le ordinate della curva normale come media np e varianza npq, dove p=p₁, q=p₂=1−p₁.