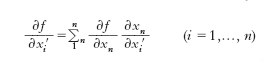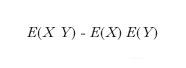covarianza

In matematica, legge di trasformazione per c., la legge secondo cui si trasformano, in ogni cambiamento di coordinate, le derivate prime di una funzione di punto in uno spazio a un qualunque numero di dimensioni. Se la funzione è f (x₁, x₂, ..., xn) e si effettua un cambiamento di coordinate dalle x₁, ..., xn alle x₁′,..., xn′, tale legge è espressa dalla relazione:

La legge di trasformazione per c. ha particolare importanza nel calcolo differenziale assoluto (in partic. per gli indici di c. ➔ tensore).

In statistica la c. tra due variabili X ed Y è un particolare tipo di legame che si valuta calcolando l’indice di c., definito da

dove con E si esprime il valore atteso (➔ probabilità). L’indice di c., diviso per σXσY (σ è la radice quadrata della varianza) dà il coefficiente di correlazione (➔ correlazione). Date n variabili X₁ ... Xn, si chiama poi matrice di c. (o di varianza e c.) la matrice quadrata di ordine n in cui il termine di riga i e di colonna j è dato dall’indice di c. tra Xi e Xj. Si definisce, infine, analisi della c. un procedimento dell’analisi statistica dei dati sperimentali (➔ varianza).