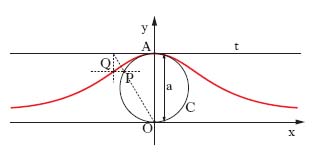
versiera

Enciclopedia on line

fig.

versiera In matematica, la cubica piana razionale, introdotta da G. Grandi, che si ottiene come segue (fig.): sia C una circonferenza, O, A, due suoi punti diametralmente opposti, t la tangente in A; considerato un punto P variabile su C, sia Q il punto d’incontro della parallella a t per P con la parallela alla retta OA per il punto d’incontro di t e della OP; al variare di P su C, Q descrive appunto la versiera. La tangente in O alla circonferenza è un asintoto, e il punto all’infinito in direzione ortogonale a questo è un punto cuspidale per la versiera. L’equazione cartesiana di tale curva è (a2+x2)y=a3, essendo a il diametro della circonferenza; l’area della regione compresa tra la v. e l’asintoto è quattro volte quella racchiusa dalla circonferenza.

Vedi anche
Guido Grandi Matematico (Cremona 1671 - Pisa 1742). Vestì l'abito dei camaldolesi e fu anche lettore di filosofia, e poi di teologia, a Firenze (1694-1700); quindi professore di filosofia (1700) e di matematica (1714) nell'università di Pisa. È conosciuto particolarmente per le opere di matematica nelle quali, tra ... perpendicolarità In geometria piana, relazione che sussiste tra rette che intersecandosi formano quattro angoli uguali. Nello spazio, la relazione di p. sussiste tra due piani se essi si intersecano formando quattro diedri uguali; si parla di p. anche tra due rette sghembe se l'una è parallela a una retta complanare ... diametro Matematica In una circonferenza o un cerchio, la lunghezza di un segmento, o il segmento stesso, che partendo da un punto della circonferenza passa per il centro e termina nel punto opposto della stessa; la lunghezza del d. d e della circonferenza c sono legate dalla relazione c=πd, dove π è il numero ...
Categorie
Tag
Altri risultati per versiera
  • Agnesi, versiera di
    Enciclopedia della Matematica (2013)
    Agnesi, versiera di curva algebrica piana del terzo ordine, definita come particolare luogo geometrico. Per la sua costruzione, si considera un punto H di una circonferenza di diametro OD e si indica con K l’intersezione della retta OH con la tangente in D alla circonferenza. Tracciate da H e K, rispettivamente, ...
  • versiera
    Dizionario delle Scienze Fisiche (1996)
    versièra [Der. di (seno)verso] [ALG] Cubica piana razionale di equazione cartesiana (a2+x2) y=a3, essendo a il diametro di una circonferenza (v. fig.); è anche detta versiera dell'Agnesi, dal nome di chi la studiò.
  • VERSIERA
    Enciclopedia Italiana (1937)
    Gino Loria . Dato un cerchio di diametro AC, su una semicorda BD a questo perpendicolare, si consideri il punto M tale che si abbia AB : BD = AC : BM; il luogo geometrico del punto M (v. fig.) è una curva considerata da G. Grandi 1671-1742), che la chiamò versoria; ordinariamente, ma a torto, è attribuita ...
Vocabolario
versièra¹
versiera1 versièra1 s. f. [aferesi dell’ant. avversiera, femm. di avversiero = avversario (eufemismo con cui viene spesso indicato il diavolo)], tosc. o letter. – 1. La moglie del diavolo, o in genere essere infernale immaginato di sesso...
versièra²
versiera2 versièra2 s. f. [der. di (seno)verso: v. verso1]. – In matematica, la cubica piana razionale avente per equazione (a2 + x2) y = a3, essendo a la lunghezza del diametro di una circonferenza; è detta anche v. dell’Agnesi, dal nome...