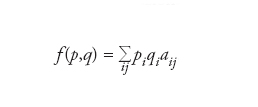utilità attesa

utilità attesa

In teoria dei giochi, le preferenze dei giocatori sugli esiti possibili si esprimono usualmente tramite funzioni di utilità. Nei giochi più semplici, quelli a due persone in cui gli esiti possibili sono la vittoria dell’uno o dell’altro, oppure il pareggio, si assume per es. convenzionalmente che la vittoria valga 1, il pareggio 0 e la sconfitta −1. È chiaro che ci sono giochi in cui non è possibile prevedere l’esito, sia pure fra giocatori perfettamente abili e razionali come quelli idealizzati dalla teoria. Basta pensare, per es., al gioco del pari e dispari, oppure alla morra cinese. D’altra parte, soprattutto nell’ipotesi di giocare ripetutamente lo stesso gioco con lo stesso avversario, è intuitivo pensare che esistano modi più o meno efficienti per giocare. Per es., nella morra cinese non giocare mai sasso sarebbe una mossa non ottimale, perché l’avversario, giocando sempre forbici, si garantisce almeno il pareggio. John von Neumann ha allora proposto di allargare il concetto di strategia: si tratta di considerare non solo le mosse possibili (strategie pure), ma anche le distribuzioni di probabilità sulle mosse stesse. A questo punto, si tratta di ricalcolare la funzione di utilità dei giocatori. La teoria della probabilità indica allora la strada per farlo: occorre considerare l’utilità attesa. Supponiamo di avere un gioco matrice in cui i pagamenti di un giocatore siano dati dai coefficienti a_ij, i=1,…m, j=1,…,n. Una coppia di strategie miste è data da (p,q), con p=(p₁,…,p_m), q=(p₁,…,p_n), p_i≥0, q_i≥0, ∑_ip_i=1 e ∑_jp_i=1. La funzione di utilità attesa del giocatore diventa in tal caso

L’idea può essere estesa ai giochi non necessariamente a somma zero.

→ Giochi, teoria dei