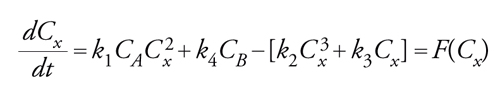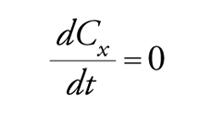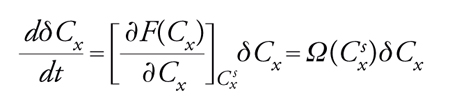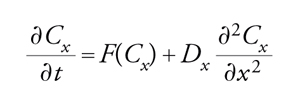Sistemi chimico-fisici: autoorganizzazione

Sistemi chimico-fisici: autoorganizzazione

In un sistema isolato, con energia costante, in assenza di scambi di materia e di energia con l'ambiente circostante, possono aver luogo fenomeni transitori fino al raggiungimento di uno stato di equilibrio in cui l'entropia è massima. In un sistema chiuso, caratterizzato dal fatto che può scambiare energia ma non materia con l'ambiente circostante, in condizioni di pressione e temperatura costanti, lo stato di equilibrio viene raggiunto quando è minima la funzione G detta energia libera di Gibbs. È comunque possibile impedire che i sistemi chimici e fisici raggiungano l'equilibrio, imponendo flussi di massa o di energia attraverso i loro confini. Un dispositivo relativamente facile da realizzare in laboratorio per conseguire tale scopo è illustrato nella fig. 1. Esso consiste in un recipiente di reazione, o reattore, sottoposto ad agitazione continua ed efficace (CSTR, Continuous stirred tank reactor), per cui le concentrazioni delle diverse specie nel suo interno si possono ritenere omogenee (viene impiegato in molti studi di cinetica chimica e di ingegneria chimica delle reazioni). I reagenti vengono pompati entro il CSTR attraverso i tubi che nella figura sono indicati come flussi di alimentazione; la reazione si svolge all'interno del reattore, mentre i prodotti e i reagenti che non hanno reagito escono attraverso lo scarico. Il reattore è circondato da una camicia d'acqua termostatata. Mediante tali dispositivi è possibile affrontare lo studio del comportamento di sistemi reagenti, la cui velocità di reazione dipende in modo non lineare dalle concentrazioni dei reagenti. Essi possono dare luogo a complesse e diverse tipologie che hanno risvegliato l'interesse di molti ricercatori.

Lo studio della velocità delle reazioni chimiche, ovvero della cinetica chimica, costituisce un vasto campo di indagine che comprende non solo l'esame dell'evoluzione nel tempo dei sistemi reagenti, ma anche il meccanismo attraverso il quale le reazioni stesse avvengono. E ciò sia dal punto di vista sperimentale, per quanto concerne le metodologie impiegate per analizzare tali fenomeni, sia teorico per quanto riguarda gli approcci concettuali utilizzati per approfondire la materia.

In questo quadro rivestono particolare importanza le reazioni autocatalitiche dove sono presenti processi di retroazione in virtù dei quali la velocità di un determinato stadio di reazione viene influenzata da una delle specie prodotte in uno degli stadi successivi. Un caso profondamente studiato è quello della reazione scoperta per caso nel 1958 dal chimico russo B. Belousov e approfondita successivamente da A. Zhabotinsky che avviene per interazione di un bromato alcalino con un sale di cerio e acido maleico. Si innesca un sistema ciclico di reazioni oscillanti che porta alla formazione di strati di colore diverso che si avvicendano nel tempo. Il meccanismo del processo è piuttosto complesso e comprende più di dieci stadi elementari, alcuni autocatalitici, che determinano una espressione matematica della velocità di reazione non lineare.

Negli ultimi cinquant'anni l'interesse verso le reazioni la cui velocità risulta espressa da relazioni matematiche non lineari è aumentato considerevolmente, soprattutto perché esse possono dare origine a una variegata e interessante tipologia di comportamenti. Questo fatto è testimoniato dal numero crescente di articoli comparsi nella letteratura scientifica di cui verrà data in questo articolo una breve rassegna.

Sistemi chimici con statistazionari multipli

Si consideri, per esempio, il semplice modello di Schlögl costituito da due reazioni elementari successive:

[1] A+2X⇄3X

[2] X⇄B.

Per i gas ideali e per le soluzioni ideali la velocità con la quale varia la concentrazione, C_x, della specie X è espressa dalla seguente equazione cinetica, derivata dalla legge dell'azione di massa:

[3] formula

ove k₁ e k₂ sono le costanti di velocità della reazione [1] e della sua inversa e analogamente k₃ e k₄ per la reazione [2], C_x, C_A e C_B sono le concentrazioni di X, A e B, rispettivamente. Questa equazione di velocità è non lineare per il fatto che vi appaiono potenze della concentrazione di X maggiori di uno. In questo caso la non linearità esercita una retroazione positiva (talvolta detta anche autocatalisi) sul primo stadio della reazione, poiché 2 molecole di X vengono trasformate in 3 molecole di X. Finché la variazione di X nel tempo è diversa da 0, si verificherà un rilassamento transitorio verso uno stato stazionario definito dalla condizione

[4] formula

che fornisce un'equazione algebrica cubica nella concentrazione di X per cui, in corrispondenza di certe scelte della pressione, del reagente A, del prodotto B e delle loro concentrazioni, potrebbero esistere 3 stati stazionari. La stabilità di ciascuno stato stazionario può essere determinata considerando la variazione temporale di una piccola deviazione

[5] δC_x=C_x−C^s_x

di C_x rispetto al suo valore nello stato stazionario, indicato con C^s_x. Poiché per C_x=C^s_x è dC_x/dt=0, attraverso uno sviluppo in serie di Taylor si ottiene:

[6] F(C_x)=0

[7] formula.

Si supponga che lo stato stazionario sia perturbato in modo tale da spostare il sistema da C^s_x a C_x=C^s_x+δC_x; in questo caso la variazione temporale della perturbazione δC_x è δC_x(t)=δC_x(t=0)exp[Ω(C^s_x)t]; pertanto, se Ω(C^s_x)〈0, il sistema è stabile, poiché la deviazione rispetto allo stato stazionario decade a 0. Al contrario, se Ω(C^s_x)>0, allora il sistema è instabile in quello stato stazionario, poiché la perturbazione rispetto allo stato stazionario cresce con il tempo. Date le concentrazioni di A e B e assegnati i valori delle costanti di velocità, si può risolvere l'equazione algebrica rispetto a C^s_x; un grafico dei valori così ottenuti è rappresentato nella fig. 2. Per certi valori di a e b, concentrazioni di A e B rispettivamente, indicati con ildeponente eq (equilibrio), il rapporto a_eq/b_eq diventa pari alla costante di equilibrio K della reazione. In corrispondenza di un certo campo di valori del rapporto a/b, esistono 3 rami di stati stazionari: i rami 1 e 3 sono stabili, mentre il ramo 2 è instabile. I punti indicati con a_m e b_m sono i cosiddetti punti di stabilità marginale. Se scegliamo il rapporto a/b in prossimità dell'equilibrio, allora un'analisi della stabilità lineare come quella eseguita in precedenza dimostra che nel caso di sistemi ideali, in cui le concentrazioni di equilibrio sono univocamente determinate, lo stato stazionario è unico e stabile.

Nelle prove sperimentali è possibile ottenere soltanto stati stazionari stabili; infatti, anche la minima perturbazione provoca un allontanamento crescente da uno stato stazionario instabile: il sistema abbandona lo stato stazionario instabile e si porta in uno stato stazionario stabile. Si supponga, quindi, che il ramo 1 degli stati stazionari stabili venga attraversato lentamente per valori crescenti di a/b: in corrispondenza del punto di stabilità marginale a_m si verifica allora una netta transizione verticale verso il ramo 3 degli stati stazionari stabili e il sistema si mantiene su questo ramo anche per ulteriori aumenti di a/b. Al decrescere di a/b, il sistema si mantiene sul ramo 3 degli stati stazionari stabili fino al raggiungimento del punto di stabilità marginale b_m, e a questo punto si verifica una netta transizione verticale fino al ramo 1 degli stati stazionari stabili. Questo tipo di transizione da un ramo degli stati stazionari stabili a un altro, in corrispondenza di posizioni differenti dei punti di stabilità marginale a_m e b_m, è un esempio di isteresi chimica. L'esistenza di una bistabilità (2 rami di stati stazionari stabili) rappresenta una sorta di commutatore chimico.

Esistono numerosi esempi di multistabilità degli stati stazionari nelle reazioni chimiche e biochimiche. Un esempio, riportato nella fig. 3, si riferisce alla reazione fra uno iodato e l'acido arsenioso e un altro all'idrolisi degli esteri catalizzata dall'enzima papaina. La dimostrazione sperimentale di bistabilità e di isteresi nei sistemi chimici fa sorgere alcune domande interessanti. Esistono criteri termodinamici che condizionano la stabilità di stati stazionari analoghi a quelli che condizionano sistemi all'equilibrio? Un altro problema da prendere in esame riguarda le fluttuazioni presenti in un sistema lontano dall'equilibrio, sia nel caso in cui sia vicino allo stato stazionario sia quando subisca una fluttuazione più ampia. In un sistema all'equilibrio vi sono relazioni tra una funzione termodinamica come l'entropia o l'energia libera di Gibbs e la probabilità di una fluttuazione termica spontanea. Esistono relazioni di questo tipo per sistemi in stati stazionari lontani dall'equilibrio?

È opportuno soffermarsi, però, su un esperimento che riguarda la stabilità relativa. Si consideri un sistema dotato di 2 stati stazionari, una parte del quale, dato un certo insieme di condizioni, si trova nello stato stazionario 1, e un'altra parte nello stato stazionario 2. Si supponga di poter realizzare un dispositivo sperimentale in virtù del quale si possano mantenere le parti del sistema nei loro rispettivi stati stazionari. Inizialmente esse sono separate, ma se la separazione viene rimossa, si può osservare che il sistema nello stato 1 si propaga e annulla il sistema nello stato 2, oppure esattamente il contrario, a seconda di quale sia lo stato più stabile. La presente descrizione dei sistemi cinetici viene detta macroscopica o deterministica e in essa l'equazione cinetica fornisce la dipendenza dal tempo della media macroscopica delle concentrazioni delle diverse specie.

Poiché, in realtà, sono presenti fluttuazioni termiche, è necessario tenere conto delle deviazioni rispetto alle medie. L'approccio abituale a questo tipo di studi è di tipo stocastico, impiega la master equation e fa uso di una funzione che esprime la probabilità P(X, t) che siano presenti molecole di X al tempo t. La descrizione stocastica dipendente dal tempo vale per processi transitori; a tempo infinito, quando il sistema si trova in uno stato stazionario, la distribuzione stazionaria è indipendente dal tempo. Per un sistema all'equilibrio, la distribuzione stazionaria è poissoniana, con un picco pronunciato in corrispondenza del valore più probabile della concentrazione che rappresenta la media macroscopica. Per sistemi bistabili, la probabilità di una distribuzione stazionaria stocastica è bimodale: un picco è situato in corrispondenza del più probabile valore macroscopico della concentrazione di uno degli stati stazionari stabili e l'altro picco in corrispondenza del valore della concentrazione macroscopica dell'altro stato stazionario stabile. L'altezza relativa dei due picchi, almeno nel limite termodinamico di un numero elevato di particelle (cioè di un sistema macroscopico), è una misura della stabilità relativa dei due stati stazionari.

Reazioni chimiche oscillanti e caotiche

Nelle reazioni chimiche oscillanti le concentrazioni delle specie chimiche variano periodicamente; queste specie possono essere indifferentemente reagenti, intermedi o prodotti di reazione. Le oscillazioni possono verificarsi in sistemi con 2 o più variabili. Anche in questo caso consideriamo un esempio semplice, cioè quello di una reazione chimica caratterizzata da 2 variabili: un substrato (reagente) S e un prodotto P; la reazione è catalizzata da un enzima E attraverso il semplice rapporto stechiometrico S+E→E+P. Il modello è un poco più semplice di quello dell'idrolisi degli esteri, in cui il substrato genera due prodotti, uno dei quali è costituito da protoni. La reazione viene catalizzata dall'enzima papaina, che si ionizza in due stadi

[8] E⇄E^′+P; E^′⇄E^″+P

ma nella quale solamente la forma E dell'enzima è attiva. Il sistema è confinato, per esempio, da una membrana, nel caso di una cellula, oppure all'interno di un CSTR, e le concentrazioni esterne del reagente S₀ e del prodotto P₀ sono mantenute costanti a valori tali che si svolga una reazione spontanea da S a P. In questo sistema le oscillazioni si verificano a causa della presenza di un meccanismo di controreazione.

Supponiamo che, a un certo istante, l'enzima si trovi prevalentemente nelle forme E^′ ed E^″: la reazione sarà lenta poiché la concentrazione della forma attiva dell'enzima E è bassa. Ma via via che la reazione si svolge, costantemente alimentata dal flusso di S₀, si ha la formazione del prodotto P, che può reagire oppure diffondere al di fuori della zona di reazione. Se le velocità delle reazioni precedenti sono elevate, allora la produzione di P sposta queste reazioni verso la produzione di concentrazioni più elevate di E, con un conseguente aumento della velocità di reazione dovuto alla catalisi da parte di E. Alla fine, la velocità di reazione sarà così elevata che il flusso di S₀ diviene insufficiente a mantenere la reazione. A questo punto le reazioni si spostano rapidamente in senso inverso, cosicché aumenta la concentrazione di P nella zona di reazione. Quindi si produrrà un rapido flusso di P fuori dal sistema, con un conseguente spostamento di E a E´ e a E´´, ritornando così alle condizioni iniziali, dopo variazioni significative delle concentrazioni di S, P ed E. Può allora iniziare un altro ciclo di oscillazioni che si susseguono fintantoché vengono mantenute le condizioni esterne.

Un esempio di reazione inorganica è quello della reazione clorito-ioduro, le cui oscillazioni temporali di alcune specie chimiche sono illustrate nella fig. 4. I meccanismi delle reazioni oscillanti possono essere abbastanza complessi per il fatto che sono costituiti da parecchi stadi elementari, in ciascuno dei quali avviene una reazione chimica attraverso una singola collisione tra reagenti. Sono state sviluppate metodologie specifiche che, attraverso la messa a punto di esperimenti, permettono di dedurre almeno la parte essenziale dei meccanismi di queste reazioni. Oltre alle variazioni periodiche delle concentrazioni di specie chimiche, se ne possono verificare diverse altre. Esistono vari tipi di attrattori periodici, caratterizzati o da una singola frequenza fondamentale, oppure da cicli limite con 2 o più frequenze fondamentali correlate razionalmente. Oscillazioni composte di vari tipi possono aver luogo in modo tale che, per esempio, le concentrazioni variano regolarmente con una grande ampiezza per un determinato periodo di tempo, al quale segue un intervallo di oscillazioni di piccola ampiezza. Un esempio interessante è costituito dalle oscillazioni improvvise nella reazione tra diossido di cloro e ioduro (fig. 5), simili ai fenomeni improvvisi che si osservano quando gli impulsi nervosi vengono trasmessi lungo un neurone. Una variazione oscillatoria non regolare delle concentrazioni in reazioni chimiche viene detta caos chimico.

Il moto caotico in sistemi fisici, meccanici, o idrodinamici e chimici, così come in molti altri campi della scienza, della medicina e delle scienze sociali, è stato oggetto di grande attenzione. Le equazioni che descrivono la cinetica chimica sono deterministiche, cioè, date le concentrazioni delle specie chimiche a un certo istante, le soluzioni delle equazioni cinetiche differenziali determinano in maniera completa le concentrazioni delle specie in ogni istante futuro. Per i sistemi caotici, però, la precisione necessaria per ottenere tali soluzioni aumenta esponenzialmente con il tempo. Due sistemi, infinitamente vicini nello spazio delle concentrazioni a un certo istante iniziale, divergono esponenzialmente al crescere del tempo. I sistemi caotici hanno comunque un attrattore stabile, verso il quale le traiettorie decadono dopo un periodo transitorio di rilassamento. Il moto in direzione di quell'attrattore non è un anello chiuso, come in un ciclo limite; un attrattore caotico è una superficie di dimensione frattale maggiore di 2. La traiettoria caotica è più complessa di quella oscillante, ma in realtà mostra una regolarità che smentisce l'immagine comunemente associata al termine caos. L'analisi della presenza del caos richiede parecchie prove severe che solitamente, perché siano efficaci, esigono un gran numero di misurazioni. Le pretese di aver scoperto un sistema caotico spesso non sono sostenute da prove concrete.

Altri tipi di sistemi reagenti

Le reazioni esaminate finora sono omogenee, perché hanno luogo in un'unica fase, quale una soluzione gassosa oppure liquida. Le reazioni eterogenee si svolgono all'interfaccia tra 2 o più fasi. Un esempio è rappresentato dall'ossidazione catalitica del monossido di carbonio su una superficie di platino che agisce da catalizzatore. La miscela gassosa di CO, O₂ e del prodotto CO₂ costituisce una fase, mentre il platino solido con i reagenti e i prodotti assorbiti è la seconda fase. Tutti i diversi tipi di reazioni non lineari, stati stazionari multipli, oscillazioni, oscillazioni composte e caos sono stati osservati anche in sistemi eterogenei. Gli esempi precedenti si riferivano a reazioni chimiche condotte a temperatura costante, cioè ai cosiddetti sistemi isotermi. La temperatura, tuttavia, può essere una variabile nei sistemi reattivi non lineari. Si consideri l'ossidazione di un composto organico, come l'acetaldeide, e si conduca la reazione in un CSTR termostatato a una certa temperatura T₀, per esempio di 250 °C.

In queste condizioni si svolge un'ossidazione a fiamma fredda, nella quale sono stati osservati stati stazionari multipli e oscillazioni di vario tipo sia delle specie chimiche sia della temperatura. Via via che i reagenti chimici O₂ e CH₃CHO entrano nel reattore, i due componenti gassosi reagiscono dando luogo a un processo di combustione esotermico: viene liberato calore e la temperatura cresce. All'aumentare della temperatura, la velocità di reazione cresce a sua volta, finché diventa così alta da esaurire tutti i reagenti presenti nel CSTR. Allora, la velocità di combustione decresce, i prodotti della reazione abbandonano il CSTR e il processo appena descritto si ripete. Infine, osserviamo che una reazione chimica condotta in un sistema chiuso che interagisce con la luce potrebbe dar vita a una multistabilità rispetto sia alle concentrazioni sia alla temperatura (fig. 6). La luce può interagire con reazioni chimiche anche per dar vita a oscillazioni e altre variazioni temporali in condizioni sia isotermiche sia non isotermiche.

Strutture spaziali in sistemi reagenti

In un sistema reagente ben agitato, le concentrazioni delle specie chimiche sono funzioni del tempo negli stati transitori, indipendenti dal tempo negli stati stazionari e dipendenti dal tempo in maniera periodica in presenza di attrattori del tipo dei cicli limite. Consideriamo ora il caso di concentrazioni di specie chimiche che dipendono sia dal tempo sia dallo spazio. Abbiamo già visto un caso, discusso in relazione agli esperimenti sulla stabilità relativa, in cui il fronte di uno stato stazionario più stabile si sposta verso uno stato stazionario meno stabile in sistemi che, in date condizioni, presentano stati stazionari multipli. Per descrivere lo spostamento del fronte ‒ che è costituito da una variazione di concentrazione nello spazio, in una certa direzione ‒ è necessario prendere in considerazione le equazioni di diffusione con reazione. Per esempio, per il modello di Schlögl descritto dalle reazioni [1] e [2], l'equazione di diffusione con reazione in una dimensione spaziale, z, ha la forma:

[9] formula

dove C_x è la concentrazione della specie X e D_x è il coefficiente di diffusione di X nella reazione.

Oltre alla propagazione del fronte, in sistemi oscillanti ed eccitabili sono stati osservati molti altri fenomeni dipendenti dal tempo e dallo spazio, quali onde chimiche, pulsazioni e fronti. Se un sistema eccitabile ha un solo stato stazionario, in corrispondenza del quale si verifica una perturbazione di una certa specie che supera un dato valore limite, si osservano ampie variazioni delle concentrazioni di tutte le specie variabili prima che si ripristini lo stato stazionario. La fig. 7 mostra la propagazione di un'onda innescata dalla reazione oscillante di Belousov-Zhabotinsky in uno stato stazionario eccitabile. L'ampiezza e la struttura del fronte della variazione di concentrazione (di Fe²⁺, misurata tramite spettroscopia di assorbimento-trasmissione) sono invarianti, poiché i 2 ripidi gradienti di concentrazione si propagano nello spazio: 1 a sinistra e 1 a destra.

Via via che i fronti si propagano, si ha un aumento di concentrazione causato dalla diffusione delle specie chimiche determinata dal brusco gradiente di concentrazione; allora il flusso entrante di materia scatena l'eccitazione della regione che si trova immediatamente prima del fronte. Ne risulta una consistente variazione delle concentrazioni delle specie reagenti prima del ritorno allo stato stazionario eccitabile e tale variazione determina la creazione di un marcato gradiente di concentrazione nella nuova regione, e pertanto causa la propagazione del fronte. Per la soluzione delle equazioni differenziali a derivate parziali corrispondenti alle reazioni con diffusione, vengono usati vari tipi di approssimazioni, che spesso sono ricondotte alle integrazioni numeriche ricavate mediante computer. L'interpretazione dei risultati ottenuti fruisce in larga misura della teoria delle biforcazioni. Le disomogeneità spaziali che si stabiliscono in sistemi lontani dall'equilibrio sono note come strutture di Turing. Un esempio di modello di Turing quasi bidimensionale è illustrato nella fig. 8 ed è stato ottenuto nelle reazioni clorito-ioduro e acido malonico.

Chimica della corrente alternata

Considereremo ora le modalità di funzionamento dei dispositivi di trasformazione dell'energia chimica e dell'energia biologica, quali possono essere, per esempio, le batterie, le pompe a protoni e i processi che avvengono durante la fotosintesi. Si consideri una reazione chimica che si svolge in una batteria: le semicelle della reazione generano una differenza di potenziale V, in corrispondenza di un certo carico sulla batteria con una forza controelettromotrice applicata E_a. La batteria produce una potenza pari a E_aI, dove I è l'intensità della corrente, (V−E_a)I è la potenza dissipata e, in condizioni stazionarie, tutte queste quantità sono costanti. Nel caso di una pompa a protoni, la potenza prodotta è pari alla differenza di potenziale tra i due lati della membrana, moltiplicata per l'intensità della corrente di protoni: la potenza assorbita è data dalla velocità d'idrolisi dell'adenosintrifosfato (ATP), moltiplicata per la variazione di energia libera di Gibbs di quell'idrolisi, e la dissipazione è pari alla differenza tra queste due quantità.

Nel funzionamento in condizioni stazionarie di una pompa a protoni, tutte queste quantità sono costanti. Nel caso di sistemi non lineari possono verificarsi stati dinamici che danno vita a oscillazioni delle concentrazioni dei prodotti intermedi, caos, oppure a uno stato stazionario, che viene chiamato 'fuoco', in cui una perturbazione decade in modo oscillatorio nello stesso stato. Si confronti l'efficienza termodinamica di una pompa a protoni (ed esistono prove sperimentali che alcune di esse si trovano in un fuoco stabile oppure in uno stato oscillante) nel caso di due diversi modi di alimentazione: una concentrazione costante oppure una concentrazione oscillante di ATP, rispettivamente. Un'analisi teorica mostra che l'efficienza, definita come il rapporto tra la potenza prodotta dalla pompa e quella immessa, può cambiare nel caso in cui l'alimentazione avvenga con una concentrazione oscillante di ATP, in relazione sia alla frequenza sia all'ampiezza delle oscillazioni di concentrazione di ATP. In condizioni oscillanti per l'ATP, il rapporto di efficienza mostra variazioni significative, in particolar modo in corrispondenza della metà e del doppio della frequenza propria del fuoco stabile, rispetto a quello che si otterrebbe in corrispondenza di un'alimentazione stazionaria di ATP alla stessa velocità complessiva di consumo del carburante, cioè dell'ATP.

Nel caso in cui si abbia un'immissione costante di ossigeno nel sistema, è possibile osservare oscillazioni di NADH (Nicotinamide adenine dinucleotide) e dell'ossigeno insoluzione. La reazione avviene e si mantiene lontano dall'equilibrio, un processo che, da un punto di vista termodinamico, è analogo a ciò che accade in una pompa biochimica, che stabilisce e mantiene un gradiente diconcentrazione ai due lati di una membrana. La variazione di energia libera di Gibbs può essere calcolata sulla base delle concentrazioni dei reagenti e dei prodotti (la concentrazione di NADH sommata a quella del NAD⁺ è costante), mentre la velocità di reazione può essere calcolata sulla base delle variazioni nel tempo delle concentrazioni dei reagenti. In questi sistemi nasce un nuovo concetto, quello di spostamento di fase tra la variazione dell'energia libera di Gibbs e la velocità di reazione; questa quantità non si osserva nel caso di cinetiche ordinarie che si svolgono in condizioni stazionarie oppure in una situazione di rilassamento monotono verso l'equilibrio.

La variazione di energia libera di Gibbs di una reazione ‒ per esempio in una pompa a protoni per il trasferimento di un protone da un potenziale chimico basso a uno più alto ‒ è proporzionale alla differenza di potenziale ai due lati della membrana, secondo quanto stabilito dall'equazione di Nernst. La velocità di pompaggio dei protoni attraverso la membrana si identifica con una corrente e l'energia prodotta dalla membrana è il prodotto del voltaggio per la corrente, ovvero l'energia libera di Gibbs che corrisponde a quel voltaggio, moltiplicata per la velocità di una pompa a protoni. Per una certa energia immessa, quella prodotta potrebbe essere alterata nei sistemi non lineari attraverso periodiche variazioni esterne delle condizioni, come, per esempio, una concentrazione variabile, anziché costante, di ATP.

Esiste pertanto la possibilità di variare l'efficienza, le concentrazioni nello stato stazionario, la dissipazione e la produzione di energia in sistemi non lineari di reazioni chimiche mediante perturbazioni delle condizioni esterne, come le concentrazioni dei reagenti. La comparsa di reazioni oscillanti in sistemi viventi potrebbe essere stata favorita dai vantaggi evolutivi rappresentati dalle variazioni di efficienza e di concentrazione nelle specie al mutare delle condizioni esterne. Nei sistemi in stato stazionario, con un decadimento non oscillante verso questo stato (nodo stabile), le efficienze, così come le altre grandezze citate, diminuiscono se le condizioni esterne, anziché essere costanti, variano. La capacità di cambiare la concentrazione media nello stato stazionario, senza variare l'immissione media di carburante, consente ai sistemi biologici di adattarsi a richieste variabili, anche in presenza di gradienti di concentrazione fissi e senza mutare radicalmente la quantità di carburante necessario. Il sistema, quindi, può adattarsi velocemente a una variazione della concentrazione necessaria a formare un determinato prodotto biologico senza cambiare la quantità media di carburante consumata.

Funzioni logiche e calcolatori ottenuti mediante cinetiche chimiche macroscopiche

Si consideri un meccanismo di reazione astratto (fig. 9) in cui A_j e B_j sono, per esempio, la forma attiva e quella inattiva di un enzima, come accade in molti meccanismi di reazioni biochimiche. Se si opera in condizioni lontane dall'equilibrio, allora la concentrazione stazionaria, poniamo di A_j, si sposta nettamente da un valore basso a un valore elevato via via che varia la concentrazione dell'enzima C_j. Questo tipo di variazione ‒ che può verificarsi solo se il sistema di reazione è lontano dall'equilibrio ‒ è analogo a quello che si riscontra in un neurone, il quale può essere attivo, allorché c'è passaggio di segnale, oppure inattivo, quando non passa alcun segnale. Pertanto, meccanismi di reazione di questo tipo sono detti neuroni chimici. L'accoppiamento di neuroni chimici può aver luogo attraverso connessioni sia di natura eccitatoria che inibitoria stabilite attraverso un coenzima, E_ij. Considerando connessioni di questo tipo tra due neuroni chimici e un terzo neurone, possiamo costruire delle porte logiche (AND, OR, NOR e altre); per esempio, in una porta AND la concentrazione di A nel neurone efferente risulterà elevata se, e solo se, lo sarà anche nei neuroni afferenti. Con porte logiche chimiche costruite sulla base di cinetiche macroscopiche è possibile progettare un decodificatore binario e un sommatore binario; la loro combinazione costituisce una macchina a stati finiti, nota anche come calcolatore universale di Turing, che può effettuare qualunque calcolo. Il calcolatore di Turing viene completato con nastri di ingresso e di uscita, detti 'cataste'; questi apparecchi possono essere costruiti anche usando neuroni chimici.

In una macchina parallela a rete neuronale, costituita da neuroni chimici accoppiati in maniera inibitoria, gli stati stazionari del sistema chimico vengono determinati da forze di accoppiamento tra neuroni scelte in precedenza. In corrispondenza di una certa condizione iniziale, per esempio un modello vicino a uno degli stati stazionari, il sistema riconosce il modello preselezionato più vicino, avvicinandosi allo stato stazionario di quel modello. Questo approccio costituisce l'attuazione chimica delle reti neuronali. Reattori ad agitazione continua, tra i quali è possibile scambio di massa, con una reazione chimica bistabile in ciascuno di essi (cioè due possibili stati stazionari stabili), possono servire come congegni per il riconoscimento di modelli. I due reattori sono connessi da tubi per il trasferimento di materia e i coefficienti della velocità di trasferimento vengono determinati attraverso l'applicazione di una regola di Hebb, derivata dai modelli che devono essere riconosciuti dal sistema. L'attuazione di funzioni di calcolo attraverso cinetiche macroscopiche può essere utile per molti scopi. Uno, in particolare, riguarda il comportamento dei sistemi viventi, incluso il cervello umano. Qualunque sia il meccanismo con il quale opera, esso può essere soltanto di natura chimica, basato essenzialmente su caratteristiche molecolari come, per esempio, le diverse configurazioni di una proteina, oppure su cinetiche macroscopiche. Gli studi descritti, quindi, aprono la possibilità di realizzare le funzioni di calcolo sulla base di trasformazioni chimiche descritte con cinetiche macroscopiche.

Bibliografia

Bergé 1986: Bergé, Pierre - Pomeau, Yves - Vidal, Christian, Order within chaos, New York, Wiley, 1986.

Borderie 1992: Borderie, Bernard e altri, Nonlinear dynamics, multiple steady states, and oscillations in photochemistry, "Journal of physical chemistry", 96, 1992, pp. 2953-2961.

Caplan 1973: Caplan, S. Roy - Naparstek, Arthur - Zabusky, Norman J., Chemical oscillations in a membrane, "Nature", 245, 1973, pp. 364-366.

Chevalier 1993: Chevalier, Tim - Schreiber, Igor - Ross, John, Towards a systematic determination of complex reaction mechanism, "Journal of physical chemistry", 97, 1993, pp. 6776-6787.

Chu 1993: Chu, Xiaolin e altri, Thermodynamic and stochastic theory of reaction-diffusion systems with multiple stationary states, "Journal of chemical physics", 99, 1993, pp. 3444-3454.

Cross, Hohenberg 1993: Cross, Michael C. - Hohenberg, Pierre C., Pattern formation outside of equilibrium, "Reviews of modern physics", 65, 1993, pp. 855-1112.

De Kepper 1990: de Kepper, Patrick - Boissonade, Jacques - Epstein, Irving R., Chlorite-iodide reaction: a versatile system for the study of nonlinear dynamical behavior, "Journal of physical chemistry", 94, 1990, pp. 6525-6536.

Dolnik, Epstein 1993: Dolnik, Milos - Epstein, Irving R., A coupled chemical burster: the chlorine dioxide-iodide reaction in two flow reactors, "Journal of chemical physics", 98, 1993, pp. 1149-1155.

Field, Burger 1985: Oscillations and traveling waves in chemical systems, edited by Richard J. Field, Maria Burger, New York, Wiley, 1985.

Foerster 1993: Foerster, Petra - Zhang, Yi-Xue - Ross, John, Experiments on relative stability in the bistable multivariable bromate-ferroin reaction, "Journal of physical chemistry", 97, 1993, pp. 4708-4713.

Gardiner 1994: Gardiner, Crispin W., Handbook of stochastic methods, 2. ed., Berlin-New York, Springer, 1994.

Gilbert 1972: Gilbert, Robert G. e altri, Interaction of sound with gas phase reactions, "Journal of chemical physics", 57, 1972, pp. 2672-2679.

Glansdorff, Prigogine 1971: Glansdorff, Peter - Prigogine, Ilya, Thermodynamic theory of structure, stability and fluctuations, New York, Wiley Interscience, 1971.

Glass, Mackey 1988: Glass, Leon - Mackey, Michael C., From clocks to chaos, Princeton, Princeton University Press, 1988.

Gray 1981: Gray, Peter, Oscillatory ignitions and cool flames accompanying the non-isothermal oxidation of acetaldehyde in a well stirred flow reactor, "Proceedings of the Royal Society of London A", 384, 1981, pp. 313-339.

Gray, Scott 1981: Gray, Peter - Scott, Stephen K., Chemical oscillations and instabilities: non-linear chemical kinetics, Oxford, Clarendon, 1990.

Harding, Ross 1990: Harding, Robert H. - Ross, John, Experimental measurement of the relative stability of two stationary states in optically bistable ZnSe interference filters, "Journal of chemical physics", 92, 1990, pp. 3579-3589.

Hjelmfelt 1991: Hjelmfelt, Allen - Ross, John - Weinberger, Edward D., Chemical implementation of neural networks and Turing machines, "Proceedings of the National Academy of Sciences USA", 88, 1991, pp. 10983-10987.

Hjelmfelt 1992: Hjelmfelt, Allen - Ross, John - Weinberger, Edward D., Chemical implementation of finite-state machines, "Proceedings of the National Academy of Sciences USA", 89, 1992, pp. 383-387.

Hjelmfelt, Ross 1994: Hjelmfelt, Allen - Ross, John, Pattern recognition, chaos, and multiplicity in neural networks of excitable systems, "Proceedings of the National Academy of Sciences USA", 91, 1994, pp. 63-67.

Hynne 1993: Hynne, Finn - Møller, T. - Sørensen, Preben G., Complete optimization of models of the Belousov-Zhabotinsky reaction at a Hopf bifurcation, "Journal of chemical physics", 98, 1993, pp. 219-230.

Kapral 1992: Kapral, Raymond - Lawniczak, Anna - Masiar, Paul, Reactive dynamics in a multispecies lattice-gas automaton, "Journal of chemical physics", 96, 1992, pp. 2762-2776.

Krischer 1992: Krischer, Katharina - Eiswirth, Markus - Ertl, Georg, Periodic perturbations of the oscillatory CO oxidation on Pt (110): model calculations, "Journal of chemical physics", 97, 1992, pp. 307-319.

Krischer 1993: Krischer, Katharina e altri, A hierarchy of trans-itions to mixed mode oscillations in an electrochemical system, "Physica D: nonlinear phenomena", 62, 1993, pp. 123-133.

Lazar, Ross 1990: Lazar, James G. - Ross, John, Experiments on the effects of external periodic variation of constraints on the thermodynamics of an oscillatory system, "Journal of chemical physics", 92, 1990, pp. 3579-3589.

Lengyel, Epstein 1993: Lengyel, Imre - Epstein, Irving R., Turing structures in simple chemical reactions, "Accounts of chemical research", 36, 1993, pp. 235-240.

Li, Ross 1991: Li, Rong-Sang - Ross, John, Chemical instabilities in closed systems with illumination, "Journal of physical chemistry", 95, 1991, pp. 2426-2430.

Luo, Epstein 1990: Luo, Yi - Epstein, Irving R., Feedback analysis for chemical oscillators, "Advances in chemical physics", 79, 1990, pp. 269-299.

Marek, Schreiber 1991: Marek, Milos - Schreiber, Igor, Cha-otic behaviour of deterministic dissipative systems, Cambridge (Mass.), Cambridge University Press, 1991.

Nitzan 1974: Nitzan, Abraham - Ortoleva, Peter J. - Ross, John, Nucleation in systems with multiple stationary states, in: Physical chemistry of oscillatory phenomena, London, Chemical Society/Faraday Division, 1974, pp. 241-253.

Noyes 1990: Noyes, Richard M., The current state of chemical oscillators, "Reaction kinetics and catalysis letters", 42, 1990, pp. 169-180.

Okamoto 1987: Okamoto, Mikizoh - Sakai, Tatsuo - Hayashi, Katsuaki, Switching mechanism of a cyclic enzyme system: role as a "chemical diode", "BioSystems", 21, 1987, pp. 1-11.

Ortoleva 1992: Ortoleva, Peter J., Nonlinear chemical waves, Chichester-New York, Wiley, 1992.

Pugh 1986: Pugh, Spenser- Schell, Mark - Ross, John, Effects of two periodic perturbations on the oscillatory combustion of acetaldehyde, "Journal of chemical physics", 85, 1986, pp. 868-878.

Ross 1988: Ross, John - Müller, Stefan C. - Vidal, Christian, Chemical waves, "Science", 240, 1988, pp. 460-465.

Ross, Schell 1987: Ross, John - Schell, Mark, Thermodynamic efficiency in nonlinear biochemical reactions, "Annual review of biophysics and biophysical chemistry", 16, 1987, pp. 401-422.

Sander 1992: Sander, Leonard M. - Imbihl, Ronald - Ertl, Gerhard, Kinetic oscillations in catalytic CO oxidation on a cylindrical Pt single crystal surface, "Journal of chemical physics", 98, 1992, pp. 5193-5204.

Schneider, Muenster 1991: Schneider, Friedemann W. - Muenster, Arno F., Chemical oscillations, chaos, and fluctuations in flow reactors, "Journal of physical chemistry", 95, 1991, pp. 2130-2138.

Steinbock 1993: Steinbock, Oliver - Zykov, Victor - Müller, Stefan C., Control of spiral-wave dynamics in active media by periodic modulation of excitability, "Nature", 366, 1993, pp. 322-324.

Tsujimoto 1991: Tsujimoto, Kim K. - Hjelmfelt, Allen - Ross, John, Measurements and calculations of oscillations and phase relations in the driven gas-phase combustion of acetaldehyde, "Journal of chemical physics", 95, 1991, pp. 3113-3223.

Tyson 1975: Tyson, John J., Classification of instabilities in chemical reaction systems, "Journal of chemical physics", 62, 1975, pp. 1010-1015.

Van Kampen 1992: van Kampen, Nicolaas G., Stochastic pro-cesses in physics and chemistry, Amsterdam, North-Holland, 1992.

Vidal, Lemarchand 1988 : Vidal, Christian - Lemarchand, Hervé, La réaction créatrice. Dynamique des systèmes chimiques, Paris, Hermann, 1988.

Vlad, Ross 1994: Vlad, Marcel O. - Ross, John, Fluctuation-dissipation relations for chemical systems far from equilib-rium, "Journal of chemical physics", 100, 1994, pp. 7268-7278.

Winfree 1973: Winfree, Arthur T., Scroll-shaped waves of chemical activity in three dimensions, "Science", 181, 1973, pp. 937-939.

Wood 1985: Wood, Peggy M. - Ross, John, A quantitative study of chemical waves in the Belousov-Zhabotinsky reaction, "Journal of chemical physics", 82, 1985, pp. 1924-1936.

Zimmerman 1984: Zimmerman, Elisabeth C. - Schell, Mark - Ross, John, Stabilization of unstable states and oscillatoryphenomena in an illuminated thermochemical system: theory and experiment, "Journal of chemical physics", 81, 1984, pp. 1327-1336.