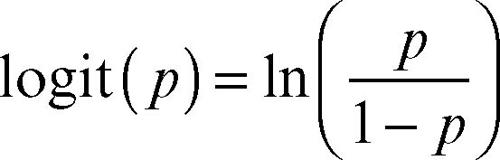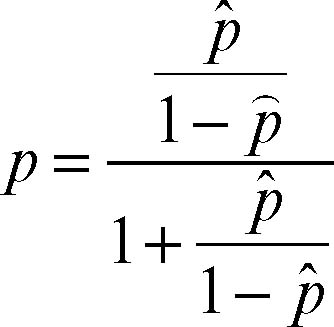regressione lineare

regressione lineare

regressione lineare in statistica, processo di determinazione di una funzione lineare che approssimi al meglio la relazione tra una variabile dipendente Y, di tipo quantitativo, e una o più variabili esplicative X₁, ..., X_k, anch’esse di tipo quantitativo. Nella sua espressione generale si cerca quindi una funzione del tipo Y = β₀ + β₁X₁+ ... + β_kX_k, dove β₀, ... β_k sono coefficienti reali da determinare. Nella regressione semplice si considera una sola variabile esplicativa e la funzione da determinare è del tipo Y = ƒ(X) che perciò, se la regressione è lineare, assume la forma Y = β₀ + β₁X. Indicando con (x_i, y_i) le osservazioni campionarie relative ai caratteri X e Y e con (x_i, ƒ(x_i)) le corrispondenti coppie di valori del modello matematico funzionale, la determinazione dei parametri β₀ e β₁ può essere effettuata con diversi metodi: si può ricorrere a metodi di → interpolazione oppure al metodo dei → minimi quadrati. Si ottiene così, per ogni osservazione campionaria, la funzione lineare y_i = β₀ + β₁x_i + ε_i, in cui ε_i è l’errore.

Nella regressione lineare semplice si assumono (oltre all’ipotesi di linearità) alcune altre ipotesi semplificatrici:

• ipotesi di non sistematicità degli errori, e che quindi la media E degli errori relativi ai singoli dati sia nulla: E(ε_i) = 0;

• ipotesi di omoschedasticità, che cioè la varianza dell’errore sia costante al variare delle osservazioni: Var (ε_i) = σ²;

• ipotesi di covarianza nulla per errori relativi a osservazioni campionarie diverse: Cov(ε_i, ε_j) = 0 per i ≠ j.

Per valutare l’affidabilità del modello si utilizzano gli opportuni indici di → scostamento.

Regressione lineare nel caso di variabile dipendente dicotomica

Se la variabile dipendente Y è dicotomica, può cioè assumere soltanto due valori, 0 o 1, «vero» o «falso», «successo» o «insuccesso», allora se ne determina la probabilità di successo P(Y) = p. Per fare ciò, si considera il rapporto tra la sua probabilità e la probabilità dell’evento complementare

detto, in statistica, anche odds. Tale valore varia tra 0 e ∞ e di esso si considera il logaritmo. Si definisce perciò la seguente funzione detta logit (da logistic unit), che è l’inversa della funzione di ripartizione collegata a una distribuzione logistica:

A essa si applica il modello di regressione lineare

in cui β₀, β₁, ..., β_k sono coefficienti da determinare. Tale modello fornisce un valore logit (p̂) nell’intervallo (−∞, +∞) e, effettuando la trasformazione inversa

si ottiene il valore p ∈ (0, 1) cercato.

Analogo al modello logit è il modello probit (da probability unit), sempre per variabili dicotomiche. In tale quadro si utilizza il modello della → distribuzione normale e si considera quindi la funzione inversa della funzione di ripartizione Φ(x) della variabile normale. Si definisce quindi

e successivamente, come nel modello logit, a esso si applica il modello della regressione lineare; infine, si opera la trasformazione inversa.