nonio
Strumento per la misurazione di frazioni delle divisioni di una scala graduata, rettilinea o circolare (si hanno in corrispondenza n. rettilinei e circolari); sono dotati di n. molti apparecchi e strumenti di misura (calibri a corsoio, goniometri, micrometri ecc.). Inventore del n. attuale è ritenuto P. Vernier (da cui deriva l’altra denominazione di verniero), che lo costruì nel 1631.
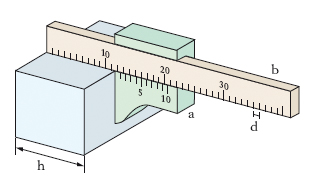
Un n. rettilineo (o lineare) consiste (v. fig.) in un corsoio mobile a, affiancato alla scala principale b (le cui tacche sono a distanza d tra loro); sul n. c’è una scala divisa in n parti uguali e lunga complessivamente (n−1) divisioni della scala principale (in fig., n=10). Quando si deve misurare una lunghezza è raro che essa abbia termine esattamente su una tacca della scala principale e perciò si deve valutare la frazione di divisione da aggiungere. Per far ciò, si fa scorrere il n. in modo che il suo zero coincida con il termine h dell’oggetto di cui si vuole misurare la lunghezza e si osserva se esiste una tacca del n. che coincide con una della scala principale; se ciò avviene per la m-ma tacca del n., la frazione di divisione da aggiungere è md/n.
I n. circolari sono fondati sullo stesso principio, salvo che tanto la scala principale quanto il n. sono circolari.