logit, modello

logit, modello

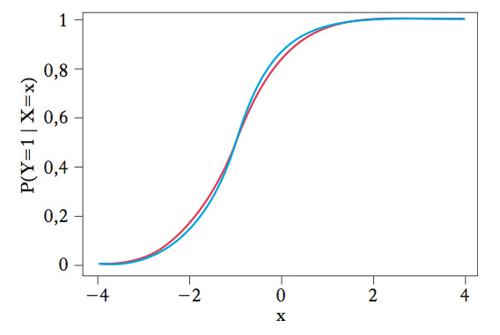
Modello di regressione non lineare (➔ regressione, modelli e stimatori di) disegnato specificamente per variabili dipendenti binarie. Se la variabile dipendente Y è binaria, ossia assume soltanto due valori (per es. maschio=0, femmina=1), un modello di regressione per Y è un modello per la probabilità che Y sia uguale a 1 (condizionatamente a un regressore X o a un insieme di regressori). Una specificazione non lineare del modello, costruita in modo tale che i valori predetti, della variabile dipendente, siano sempre compresi tra 0 e 1, è in questo caso più adeguata di una lineare, che potrebbe produrre valori predetti negativi o superiori a 1 per la probabilità π(x)=P(Y=1∣X=x). In particolare, nel modello l. la probabilità è specificata tramite una funzione logistica: π(x)=e^α+βX∕(1+e^α+βX). Una particolarità della specificazione l. consiste nel fatto che essa comporta la linearità (➔) di una trasformazione della distribuzione di probabilità di Y (condizionata a X), chiamata ‘logaritmo degli odds’, log(π(x)∕(1−π(x)) tale funzione è lineare e uguale a α+βX. Un altro modello di regressione usato frequentemente per trattare variabili dipendenti binarie è il modello probit (➔ probit, modello), che specifica la probabilità π(x) tramite la funzione di ripartizione gaussiana (➔ gaussiana, distribuzione). La figura 1 mostra i grafici della funzione logistica e della funzione di ripartizione gaussiana al confronto per α=0, β=1. La distribuzione logistica è stata standardizzata in modo da avere varianza unitaria.