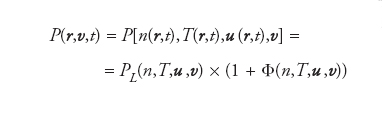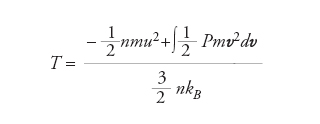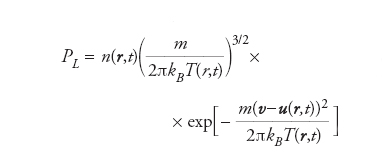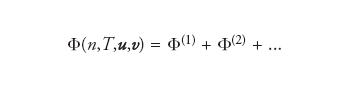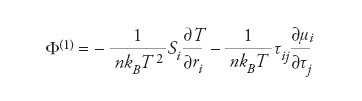metodo di Chapman-Enskog

metodo di Chapman-Enskog

Procedura ispirata da un’idea di David Hilbert, che consiste nel cercare una soluzione dell’equazione di Boltzmann assumendo che la dipendenza spaziale sia determinata solo dai ‘campi idrodinamici’:

formula [1]

dove n=∫Pdv è il campo di densità, u=(1/n)∫vPdv è il campo vettoriale di velocità macroscopico e

formula [2]

è il campo di temperatura. La soluzione di ordine zero P_Λ(n,T,u,v) è l’equilibrio locale

formula [3]

Il termine perturbativo Φ viene cercato nella forma di un’espansione in gradienti di ordine crescente rispetto ai campi macroscopici n,u,T:

formula [4]

dove Φ⁽¹⁾ è lineare nelle prime derivate spaziali dei campi, Φ⁽²⁾ è quadratico nelle prime derivate e lineare nelle seconde derivate, e così via. Queste derivate sono moltiplicate da coefficienti (legati ai cosiddetti coefficienti del trasporto dell’idrodinamica) a loro volta funzioni di n,u,T. Ricordiamo che l’equilibrio locale [3], inserito nell’equazione di Boltzmann, annulla in ogni punto l’integrale di collisione: da qui è possibile ricavare, proiettando l’equazione di Boltzmann su 1, v e v², le equazioni di Euler per l’evoluzione di n,u,T ovvero l’idrodinamica senza dissipazione. Il passo successivo della procedura di CE consiste nel sostituire nell’equazione di Boltzmann la soluzione [1] in cui l’espansione [4] è troncata al primo ordine: qui si devono trascurare i termini non lineari in Φ⁽¹⁾, quelli non lineari nelle prime derivate spaziali e quelli di qualunque ordine nelle derivate spaziali di ordine superiore al primo. Così facendo, e usando le equazioni di ordine zero per esprimere le derivate temporali dei campi, si ottiene un’espressione per Φ⁽¹⁾ del tipo

formula [5]

dove S_ι e τ_ιξ sono coefficienti determinati dalla stessa equazione di Boltzmann. Il troncamento dell’espansione al primo ordine risulterà tanto più buono, tanto più piccolo è il rapporto ℓ/ℒ (numero di Knudsen), dove ℓ è il cammino libero medio e ℒ una lunghezza idrodinamica caratteristica. La determinazione di ognuno dei coefficienti S_ι e τ_ιξ richiede la soluzione di un’equazione integrale piuttosto complicata, che non può essere affrontata in questa sede. Basti sapere che da S_ι e τ_ιξ si ottengono i coefficenti del trasporto, fondamentali per l’idrodinamica, in particolare la viscosità di bulk e la conducibilità termica. Nelle equazioni di conservazione del momento e dell’energia, ottenute proiettando l’equazione di Boltzmann su mv e su mv²/2, appaiono infatti i flussi dissipativi: una volta nota la soluzione al primo ordine P_Λ(1+Φ⁽¹⁾), è sufficiente inserirla nell’espressione di questi flussi, ottenendo dei termini proporzionali ai gradienti spaziali dei campi: il flusso di calore risulta proporzionali al gradiente di temperatura (legge di Fourier), mentre i flussi di momento risultano proporzionale ai gradienti del campo di velocità (cosiddetta legge di Newton).

→ Materiali granulari