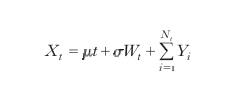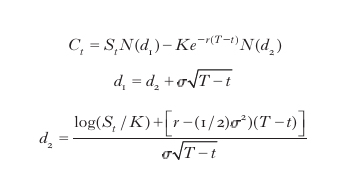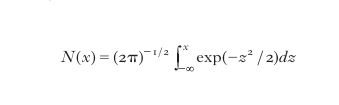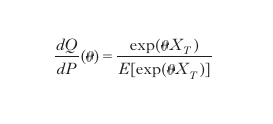Matematica finanziaria

Matematica finanziaria

Nel corso degli ultimi anni la matematica finanziaria si è notevolmente ampliata nei contenuti e negli strumenti d'analisi. La motivazione di ciò è riconducibile al riconoscimento del ruolo centrale dell'incertezza in tutti gli aspetti economici e finanziari. La visione stocastica della realtà finanziaria ha portato all'introduzione di un nuovo concetto di rischio, alla riformulazione di vecchi problemi in termini stocastici e all'adozione sistematica dei metodi statistici e della probabilità, in contrapposizione con la tradizionale teoria deterministica. Se lo strumento è quello dell'analisi stocastica, dal punto di vista dei contenuti, i nuovi sviluppi si possono dividere in alcune aree principali: valutazione e arbitraggio, gestione dei portafogli finanziari, ingegneria finanziaria.

Un problema centrale della moderna teoria finanziaria consiste nel determinare i prezzi delle attività finanziarie. Il principio guida è quello di non arbitraggio: in mercati sufficientemente concorrenziali, portafogli con flussi di cassa simili devono avere prezzi simili. Deviazioni sistematiche da un tale principio darebbero luogo a illimitate opportunità di guadagno contro ogni evidenza empirica.

A ogni attività finanziaria si può associare un tasso atteso e una variabilità di rendimento (o varianza). Questi sono gli elementi fondanti della teoria microeconomica delle scelte di portafoglio fondata da H.M. Markowitz (1952). In generale, gli investitori richiedono un maggior rendimento a fronte di una maggiore rischiosità. L'intuizione è che portafogli opportunamente diversificati consentono una rilevante riduzione del rischio senza dover rinunciare alla redditività. Se il portafoglio contiene attività e passività, si parla di asset & liability management (ALM) e si considerano tra gli obiettivi della gestione molteplici rischi da minimizzare (variabilità dei prezzi dei titoli, duration, inflazione, rischio di cambio e d'insolvenza ecc.).

Una delle aree più attive riguarda la costruzione di nuovi prodotti rivolti all'industria finanziaria e anche agli operatori economici, finalizzati a particolari problemi sia di finanziamento sia di copertura dei rischi.

La modellizzazione finanziaria oltre il moto browniano

Sviluppi importanti nel campo della finanza e della matematica applicata si sono avuti con l'adozione di processi stocastici con salti nell'analisi delle fluttuazioni dei mercati finanziari. Nel panorama dei processi stocastici utilizzati per modellizzare e analizzare i fenomeni aleatori che si osservano in ambito finanziario ed economico, indubbiamente il moto browniano occupa una posizione di rilievo. Un moto browniano è un processo stocastico, ovvero una famiglia di variabili casuali W_t dipendenti dal tempo t, avente incrementi indipendenti e stazionari che seguono una distribuzione di probabilità gaussiana.

Lo studio del moto browniano ha visto notevoli sviluppi e molte applicazioni alla finanza fin da quando L. Bachelier in Théorie de la spéculation (1900) propose di modellizzare il prezzo S_t dei titoli quotati alla Borsa di Parigi secondo l'equazione:

S_t = S_∘+ σW_t  [1]

in cui σ è un coefficiente reale positivo, detto volatilità. La versione moltiplicativa del modello di Bachelier ha condotto al più noto modello di Black-Scholes, in cui S_t segue un moto browniano geometrico:

S_t = S_{∘exp(μt +} σW_{t )}  [2]

essendo μ un coefficiente reale, detto drift. Una proprietà importante del moto browniano è la continuità delle sue traiettorie (t → W_t) come funzioni del tempo. Questo fatto consente una distinzione tra le traiettorie del processo [2] e quelle osservate per le quotazioni reali di un titolo: queste ultime presentano infatti un maggior numero di repentine variazioni, che si manifestano come discontinuità (salti) delle traiettorie. Le differenze diventano più evidenti se si esegue un'analisi delle quotazioni infragiornaliere, analizzando gli incrementi del logaritmo del prezzo, che rappresentano le grandezze rilevanti per un investitore: r_t(Δ)=ln(S_t+Δ)−ln(S_t), dove Δ esprime una scala di tempo variabile da pochi secondi fino a diversi giorni. Data la necessità di disporre di informazioni e dati finanziari con una sempre maggior frequenza, le scale di tempo rilevanti nelle applicazioni sono diventate tali da non poter trascurare il fenomeno descritto in precedenza. Il modello [2] non è il solo modello a tempo continuo: modelli basati su diffusioni di Markov non lineari, nei quali la volatilità può dipendere sia dal prezzo sia dal tempo attraverso una funzione di volatilità locale, σ=σ(S_t, t), sono stati proposti da B. Dupire (1994), E. Derman e I. Kani (1994). Un'altra possibilità viene fornita da modelli a volatilità stocastica σ_τ, nei quali il prezzo St è componente di un processo stocastico a due dimensioni (S_t, σ_τ).

Questi modelli presentano proprietà statistiche più flessibili del modello [2] e condividono con il moto browniano la continuità delle traiettorie. Tuttavia, assumendo che il prezzo segua una traiettoria continua, si trascura l'elevata variabilità rilevabile nelle quotazioni reali, nella quale è concentrata la maggior parte del rischio connesso all'attività finanziaria. Altri elementi a sostegno della discontinuità dei prezzi derivano da un'analisi empirica dei rendimenti. La loro distribuzione presenta il fenomeno delle heavy tails, cioè un'elevata probabilità che si verifichino ampi movimenti del prezzo. Infatti si osserva che la densità di probabilità dei rendimenti f(r) tende a zero secondo un indice di decadimento α al tendere di |r| all'infinito: f(r)∼c/ⅠrⅠ^1+α. L'autocorrelazione lineare tra i rendimenti risulta molto piccola; inoltre si può riscontrare il fenomeno del volatility clustering, per cui ampie (o piccole) variazioni di prezzo sono seguite da ampie (o, rispettivamente, piccole) variazioni di segno opposto. Questi e altri fatti evidenziano una significativa deviazione dall'ipotesi di normalità dei rendimenti.

Studi di carattere empirico hanno condotto a proporre nuovi modelli parametrici per la distribuzione di probabilità dei rendimenti, r_t(Δ), come la distribuzione t-Student, le distribuzioni α-stabili e iperboliche e le distribuzioni inverse gaussiane (Barndorff-Nielsen 1998). La presenza di salti nei prezzi e la necessità di catturare le evidenze empiriche hanno portato a introdurre un'estensione del modello [2] in cui l'esponente è sostituito da un più generale processo stocastico, detto di Lévy, cioè un processo stocastico X_t, con t≥0, a tempo continuo, avente incrementi indipendenti e stazionari, stocasticamente continuo. Un elemento caratterizzante di ogni processo di Lévy è quello del numero atteso di salti ν(dx), di ampiezza dx, a unità di tempo, espresso attraverso la misura ν. I modelli finanziari con salti studiati in letteratura possono essere divisi in due categorie principali: modelli di diffusione- salto e modelli ad attività infinita.

Modelli di diffusione-salto. - L'evoluzione normale dei prezzi è basata su un processo di diffusione il cui andamento è interrotto da salti che rappresentano eventi rari, dovuti a particolari accadimenti che si rilevano nel mercato finanziario e che avvengono a intervalli di tempo aleatori. Un modello di questo tipo ha la forma:

formula [

3]

in cui N_t è un processo di Poisson che conta i salti di X_t e le Y_i (i=1,2,3,…) sono variabili aleatorie indipendenti e identicamente distribuite che rappresentano le ampiezze dei salti. Per es., nel modello di Merton i salti Y_i seguono una distribuzione gaussiana. Data la semplicità della loro struttura dinamica, questi processi di prezzo sono stati utilizzati per costruire efficienti procedure Monte Carlo per valutare complesse opzioni finanziarie.

Modelli ad attività infinita. - In questa categoria si trovano modelli aventi un numero infinito di salti in ogni intervallo di tempo. Questa classe contiene esempi di modelli in grado di descrivere in modo più realistico i prezzi per varie scale temporali (Δ). Uno di questi modelli si ottiene subordinando un moto browniano con un processo di Lévy L_t, detto subordinatore, le cui traiettorie sono crescenti. Il modello prende la forma seguente:

X_t = μL_t + σW(L_t).  [4]

Il subordinatore ha il significato del tasso di informazione proveniente dal mercato nel tempo. Appartiene a questa classe il modello variance gamma, uno dei principali modelli introdotti nella recente letteratura finanziaria.

La valutazione di strumenti finanziari nei modelli con salti

La principale motivazione per l'introduzione di sofisticati modelli stocastici a tempo continuo in finanza è stata quella di sviluppare metodi efficienti per valutare i derivati finanziari (derivatives o contingent claims), il cui valore dipende dal prezzo del titolo su cui essi sono scritti. Tra i più diffusi strumenti derivati, quotati nelleBorse di tutto il mondo, si trovano le opzioni. Un'opzione è un contratto che, nella forma più semplice, consiste nella cessione da parte di un venditore (writer) a un acquirente (buyer) del diritto di acquistare (opzione call) o di vendere (opzione put) una quantità di un certo strumento finanziario a un prezzo prefissato (d'esercizio) entro una certa data futura (opzione americana) o allo scadere di essa (opzione europea). Per comprendere il tipo di copertura realizzato dall'opzione, si osservi che se T è la data di scadenza, ST il prezzo in T del titolo su cui l'opzione è scritta, K il prezzo d'esercizio, i valori della call e della put alla data di scadenza saranno:

C_t = max(∘, S_T-K) P_t = max(∘, K - S_T). [5]

In particolare, se S_T>K la call si dice in-the-money e l'esercizio dell'opzione darà un ricavo di S_T −K, a fronte di un costo limitato, pari al prezzo dell'opzione. Se S_T〈K la call si dice out-of-the-money ed essa non sarà esercitata. Il contrario accade per un'opzione put. L'aggiunta di un'opzione put a un portafoglio costituito dall'azione su cui la put è scritta, assicura, a scadenza, un ricavo non inferiore a K (assicurazione di portafoglio), mentre la vendita allo scoperto di un'azione e l'acquisto di una call assicura a scadenza un esborso non superiore a K. L'acquisto di una call e la vendita di una put dà luogo a una posizione equivalente a un contratto a termine (futures). Risulta evidente la duplice caratteristica speculativa e assicurativa delle opzioni. Il metodo di costruzione di un portafoglio che replica i flussi di cassa di un altro titolo o portafoglio è stato utilizzato da F. Black e M. Scholes per determinare analiticamente il prezzo di una call di tipo europeo, in funzione del prezzo del titolo sottostante e della sua dinamica temporale. Specificamente, considerando un'evoluzione continua del tempo, sia C (t,T,K,S_t) il prezzo al tempo t di una call europea con scadenza T (>t) e prezzo d'esercizio K, scritta su un'azione di prezzo S_t. Si costruisca un portafoglio dato da un'unità dell'azione e dalla vendita scoperta di 1/Δ(t) unità della call, in cui Δ(t) è la derivata del prezzo C rispetto a S. Il portafoglio, aggiustato continuamente nella quantità della call, sarà protetto (hedged portfolio) dai movimenti del titolo azionario in quanto il suo valore V_t=S_t−C_t/Δ(t) ha derivata nulla rispetto a S_t. In assenza di altre fonti di incertezza oltre l'andamento di S_t, e in assenza di opportunità di arbitraggi non rischiosi, il tasso istantaneo di rendimento di V_t dovrà essere il tasso prevalente sui titoli privi di rischio r, ovvero dV_t/V_t=rdt. Tale condizione, assumendo che il prezzo S_t segua l'equazione [2], consente di ricavare una formula per il prezzo call:

con

formula [

6]

dove

è la funzione di distribuzione normale standard. Il prezzo della put europea si ottiene in base a considerazioni di non arbitraggio (put-call parity) da quello della call. La formula di Black e Scholes ha avuto una vastissima risonanza sia scientifica sia operativa. Data l'accresciuta volatilità dei mercati, le opzioni sono oggi largamente utilizzate tanto come strumenti di speculazione quanto come strumenti di copertura dai rischi di mercato, legati, per es., a oscillazioni nei cambi (currency options) oppure nei tassi d'interesse (cap floors, collars, swaptions), senza precludere all'investitore la possibilità di guadagnare nel caso di movimenti favorevoli del titolo sottostante. Nelle strategie di copertura, la derivata del prezzo call rispetto al prezzo del sottostante indica la proporzione da mantenere tra quantità acquistate (vendute) del titolo e quantità vendute (acquistate) dell'opzione affinché, per piccole variazioni di S, profitti e perdite si compensino e il portafoglio sia immunizzato (delta-hedging). Tale strategia non garantisce una copertura completa, tanto per approssimazioni nella formula [6] (o altre simili) quanto per gli errori di stima della volatilità σ. La disponibilità di mercati di opzioni semplici (plain vanilla) sempre più liquidi e la presenza di rischi non completamente eliminabili nell'attività di trading hanno portato a riconsiderare le metodologie di pricing ed hedging, inquadrando il problema della valutazione dei derivati finanziari in un contesto più generale rispetto al modello di Black-Scholes. La logica che guida la scelta di un modello di pricing si differenzia sostanzialmente da quella dei tradizionali modelli econometrici: un modello di pricing è uno strumento utilizzato per descrivere il valore delle opzioni quotate sui mercati, legando i prezzi sulla base di un'ipotesi di assenza di arbitraggio. Una delle conseguenze fondamentali di tale principio è che il prezzo di uno strumento finanziario si esprime come il valore atteso dei suoi flussi di cassa futuri, rispetto a un'appropriata misura di probabilità. Per illustrare questo aspetto, si consideri un mercato le cui possibili evoluzioni tra 0 e T sono descritte da uno spazio di probabilità (Ω, F, P), in cui F (σ-algebra) contiene tutte le informazioni riguardanti il comportamento dei prezzi, mentre P esprime la misura di probabilità in tale spazio. Sia F_t l'informazione generata dalla storia del prezzo dei titoli fino al tempo t (per cui F=F_T). In questo contesto, il valore alla scadenza T di un derivato finanziario (payoff) può essere rappresentato da una variabile aleatoria H_T definita al tempo T. Per es., il payoff di un'opzione call è H_T=max(0, S_T−K). Un modello di pricing definisce una legge che a ogni istante di tempo t (≤T) attribuisce un valore V_t(H_T) del derivato al tempo t. È possibile dimostrare che ogni regola di pricing consistente con ipotesi minimali tra le quali vi è quella di poter conoscere Vt(HT) disponendo soltanto dell'informazione fino al tempo t, e la condizione per cui V_t(H_T)≥0 se H_T≥0, deve verificare la seguente relazione per un'opportuna misura di probabilità Q:

V_t(H_T) = e^-r(T-t)E^Q[H_T|F_t]  [7]

dove E^Q[.|F_t] denota il valore atteso condizionale rispetto alla storia dei prezzi fino al tempo t, mentre r è il tasso prevalente sui titoli privi di rischio. Uno dei risultati portanti della moderna teoria finanziaria asserisce che un mercato finanziario, in cui i processi di prezzo verificano opportune condizioni, è consistente con il principio di non arbitraggio se - e solo se - esiste una misura di probabilità Q (equivalente a P) tale che valga la [7] e i prezzi attualizzati dei titoli nel mercato siano delle martingale rispetto a Q. Questo risultato stabilisce un'equivalenza tra il concetto finanziario di assenza di arbitraggio e la nozione di misura di martingala equivalente. La misura Q, che in termini finanziari è detta risk-neutral, è ottenibile da un'osservazione dei prezzi dei derivati al tempo t=0. Oltre alla nozione di non arbitraggio, vi è un altro importante concetto originariamente presente nel modello di Black-Scholes, quello di completezza. Secondo questa nozione, ogni contingent claim H ammette una strategia di investimento in grado di replicarne il valore. Mentre molti modelli di pricing di derivati verificano il principio di non arbitraggio, solo pochi sono modelli completi: i modelli a volatilità stocastica, di diffusione-salto e i modelli di Lévy esponenziali. L'impossibilità pratica di realizzare un hedging perfetto di un'opzione senza incorrere in rischi rende irrealistica l'ipotesi di completezza del mercato. A differenza dei modelli completi, in cui la misura Q è unica, nei modelli di Lévy esponenziali l'insieme delle misure risk-neutral risulta infinito; questo fatto fornisce ai modelli una notevole flessibilità nella loro applicazione. Infatti nei modelli completi, come il modello di Black-Scholes, i prezzi delle opzioni sono unicamente determinati e spesso non coincidono con i prezzi quotati sui mercati finanziari. Nei modelli di diffusione la misura Q è ottenuta cambiando il coefficiente di drift (μ) del processo di prezzo. Nei modelli con salti, questa tecnica di aggiustamento del drift non tiene conto della valutazione del rischio legato ai salti del prezzo. Un'ampia varietà di misure di martingala equivalenti si ottiene quindi alterando la distribuzione dei salti. Una trasformazione analoga a quella del drift nel moto browniano geometrico è quella indotta dalla trasformata di Esscher.: se X_t=ln(S_t) segue un processo di Lévy, la misura Q è definita dalla sua derivata (di Radon-Nikodym) rispetto alla misura P:

formula [

8]

per un opportuno numero reale θ. La trasformata di Esscher è usata per costruire misure risk-neutral in modelli di Lévy esponenziali (Satō 1999). L'impossibilità di realizzare una completa immunizzazione finanziaria nei mercati reali ha condotto a rivedere tale questione in maniera più realistica, approssimando un determinato payoff con una strategia di compravendita delle attività sottostanti e specificando un modo di misurare e minimizzare il rischio. Differenti modi di misurare il rischio conducono a diversi criteri di copertura: superhedging, massimizzazione dell'utilità ed hedging quadratico. Secondo questi metodi, il valore dell'opzione si divide in due componenti: il costo della strategia di immunizzazione e un premio per il rischio, richiesto dall'investitore a copertura del rischio residuo (non eliminabile). L'ampia letteratura nazionale e internazionale che si va accumulando su questi aspetti e la continua nascita di riviste di m. f., finanza stocastica e finanza quantitativa testimoniano un grande interesse per la materia e importanti prospettive di sviluppo lungo le direzioni indicate.

bibliografia

R. Merton, Option pricing when underlying stock returns are discontinuous, in Journal of financial economics, 1976, 3, pp. 125-44.

O. Barndorff-Nielsen, Processes of normal inverse gaussian type, in Finance and stochastics, 1997, 2, pp. 41-68.

F. Delbaen, W. Schachermayer, The fundamental theorem of asset pricing for unbounded stochastic processes, in Mathematische Annalen, 1998, 312, pp. 215-50.

K. Satō, Lévy processes and infinitely divisible distributions, Cambridge 1999.

D. Madan, Financial modelling with discontinuous price processes. Lévy processes-theory and applications, Boston 2001.

R. Cont, P. Tankov, Financial modelling with jump processes, London 2004.