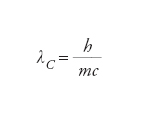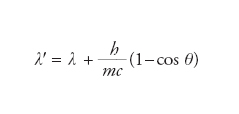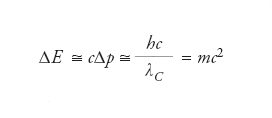lunghezza d'onda Compton

lunghezza d’onda Compton

La costante di Planck h e la velocità della luce nel vuoto c consentono di associare a una particella di massa m una grandezza caratteristica, detta lunghezza d’onda Compton λ_C e definita come

Il nome trae origine dal fatto che questo parametro determina lo spostamento Compton della lunghezza d’onda λ per luce incidente idealmente su particelle libere, secondo la relazione

dove λ′ denota la lunghezza d’onda della luce diffusa a un angolo θ rispetto alla direzione di incidenza. La verifica sperimentale di questa relazione è ritenuta giustamente uno dei capisaldi della fisica del Novecento, in quanto ha reso possibile associare un impulso di intensità h/λ ai fotoni, le particelle responsabili della radiazione luminosa di cui Planck ed Einstein avevano già identificato l’energia, pari a hc/λ. Per un nucleo di idrogeno, per es., λ_C≅2×10⁻¹⁶m, circa un quinto del suo raggio caratteristico, mentre per un elettrone λ_C≅4×10⁻¹⁴m. La lunghezza d’onda Compton λ_C ha un ruolo centrale nello studio di fenomeni all’interfaccia tra relatività speciale e meccanica quantistica, e in particolare nella descrizione delle forze tra particelle. È un risultato di valenza generale che queste forze sono mediate da scambi di altre particelle in modo tale che, se m è la loro massa, i loro effetti divengono trascurabili a distanze maggiori della loro lunghezza d’onda Compton λ_C. Il fotone, per es., è ritenuto di massa nulla proprio in quanto il raggio d’azione delle forze elettromagnetiche è illimitato, mentre i bosoni W e Z che mediano le interazioni deboli sono massivi e producono effetti che sono direttamente avvertibili solo a distanze non superiori alle dimensioni tipiche di un nucleo atomico. La lunghezza d’onda Compton λ_C identifica inoltre la minima localizzazione spaziale possibile per una particella di massa m. Se infatti si tentasse di effettuare una misura di posizione con incertezza inferiore a λ_C, le fluttuazioni quantistiche dell’impulso e quindi dell’energia finirebbero in generale per disintegrarla, coerentemente con il principio di indeterminazione, in base al quale

Pertanto un oggetto si comporta in modo essenzialmesnte ‘quantistico’ se la sua estensione spaziale è molto minore della corrispondente λ_C, o viceversa in modo essenzialmente ‘classico’ se la sua estensione spaziale è molto superiore a λ_C. La prima situazione si realizza per le particelle elementari del Modello Standard, mentre l’altra è tipica dei solitoni presenti in alcune sue estensioni.

→ Stringhe, teoria delle