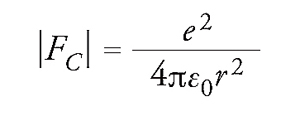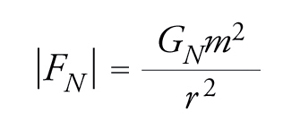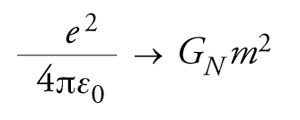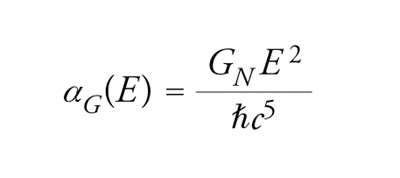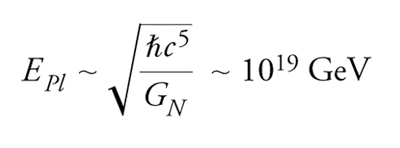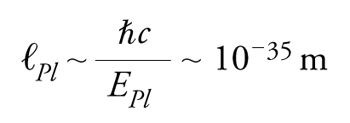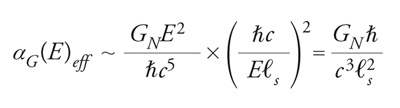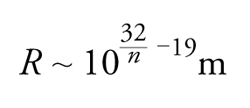Stringhe, teoria delle
Stringhe, teoria delle
La descrizione delle particelle elementari è stata un obiettivo centrale della fisica almeno a partire dalla fine del XIX sec., con la scoperta dell'elettrone. Il nucleo atomico fu scoperto analizzando processi d'urto, lo strumento principe per lo studio delle interazioni delle particelle elementari, il cui ruolo è fondamentale dal punto di vista sia sperimentale sia teorico. La meccanica quantistica ha introdotto in questa descrizione alcune radicali novità, assegnando alle particelle proprietà ondulatorie oltre che corpuscolari. A partire dalla fine degli anni Venti del XX sec., si è inoltre presentata l'esigenza di armonizzare in modo sistematico questi nuovi principî con la relatività speciale. Ne è scaturita la teoria quantistica dei campi, che associa le particelle a quanti di energia dei campi d'onda corrispondenti rendendo manifesta l'assoluta identità di tutte le particelle di uno stesso tipo. Dagli anni Trenta si è quindi cercato a più riprese di giungere a una teoria di 'tutte' le particelle elementari: esperimenti a energie sempre più elevate hanno mostrato che alle poche particelle che compongono la materia ordinaria, vale a dire elettroni, protoni e neutroni, se ne aggiungono moltissime altre, la maggior parte delle quali è instabile, con tempi di disintegrazione spontanea al più di qualche milionesimo di secondo.
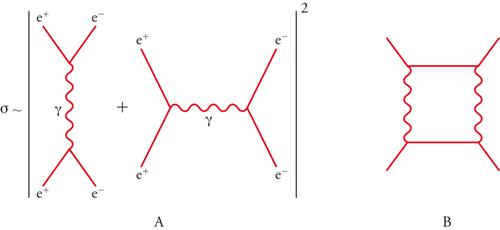
La descrizione in termini di campi assegna alle particelle un limitato numero di attributi, tra i quali la massa, lo spin e uno o più tipi di carica. Le stesse interazioni tra particelle, inoltre, sono indotte da scambi di altre particelle: per esempio, l'ordinaria repulsione coulombiana tra due elettroni può essere considerata il risultato di uno scambio di fotoni. Questa rappresentazione è alla base della tecnica assai suggestiva dei diagrammi di Feynman, che consente di collegare le probabilità di reazione, note come sezioni d'urto, a processi elementari nei quali le particelle reagenti generano altre particelle in stati intermedi. Alla somma dei diagrammi relativi a un certo processo la teoria associa un'ampiezza di probabilità, vale a dire un numero complesso il cui modulo al quadrato determina essenzialmente le sezioni d'urto. Con il proliferare delle particelle soggette alle interazioni forti, l'applicazione di tali metodi è risultata a lungo limitata, a causa dell'estrema intensità di queste forze nucleari. Negli anni Sessanta sono stati dedicati molti sforzi al problema di caratterizzare in termini generali le sezioni d'urto, o più precisamente la matrice S, una collezione delle corrispondenti ampiezze di probabilità. La teoria delle stringhe ha avuto origine proprio in questo ambito, quando appariva impossibile il ricorso alla teoria quantistica dei campi e ai corrispondenti diagrammi di Feynman per le interazioni forti.
Interpretazione in termini di corde vibranti
Nel 1968 il fisico teorico Gabriele Veneziano, cercando esempi concreti di matrici S, riconobbe una sorprendente relazione tra la descrizione matematica di un processo d'urto tra due particelle e l'integrale euleriano, una nota funzione di due variabili complesse definita, per Re(s)>0 e Re(t)>0, nel modo seguente
[1] B(s,t) = ∫01x s −1(1−x)t −1 dx.
Nella corrispondenza identificata da Veneziano, le variabili s e t nella [1] caratterizzano rispettivamente le energie delle particelle coinvolte nell'urto e gli angoli di impatto. In generale, i diagrammi di Feynman dipendono da queste grandezze, ma non manifestano individualmente alcuna simmetria per lo scambio di esse, là dove la peculiarità della funzione B è proprio la sua simmetria per lo scambio delle due variabili s e t, detta in questo contesto dualità planare. B(s,t) possiede inoltre infiniti poli, per s,t=0,−1,−2,…, nell'intorno dei quali si comporta essenzialmente come la funzione 1/z in prossimità dell'origine z=0. Singolarità di questo tipo sono caratteristiche dei contributi di ordine più basso, senza loop o ad albero, come i due diagrammi a sinistra nella fig. 2, i cui stati intermedi coinvolgono altrettanti tipi di particelle, ma una alla volta, e segnalano appunto il loro scambio. Fu quindi presto chiaro che l'ampiezza di Veneziano aveva origine da una teoria molto più complessa di quelle precedentemente note, con infiniti tipi di particelle tutte bosoniche e di masse e spin crescenti.
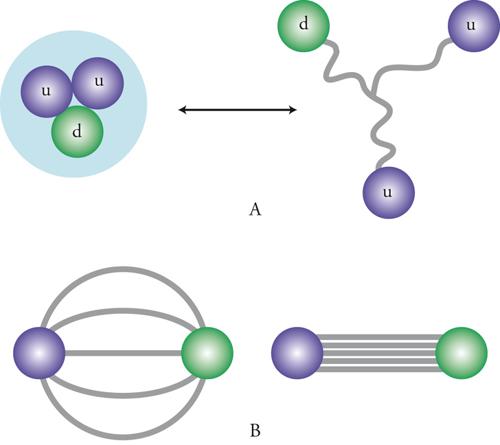
Poco dopo il lavoro di Veneziano, Joel Shapiro e Miguel Virasoro ottennero una generalizzazione di B(s,t), anch'essa con infiniti poli, che dipende simultaneamente e in modo totalmente simmetrico da tre variabili associate al processo d'urto, proprietà questa detta dualità non planare. Nei due anni successivi, diversi gruppi di ricercatori riuscirono a costruire altri tipi di ampiezze, ad albero e con loop. Per alcuni anni le simmetrie di tali ampiezze giustificarono il nome di modelli duali per la nuova teoria e le sue generalizzazioni, e lo sviluppo di questo formalismo deve molto a fisici italiani quali Daniele Amati, Sergio Fubini e Paolo Di Vecchia. L'interpretazione di questi risultati divenne più chiara nel 1970, grazie ai contributi di Yoichiro Nambu, Holger B. Nielsen e Leonard Susskind. Questi studiosi osservarono che le sorprendenti proprietà delle nuove ampiezze sono naturali per diagrammi di Feynman nei quali le linee descritte da particelle siano sostituite da tubi (descritti da stringhe chiuse) o da nastri (descritti da stringhe aperte), suggerendo che l'ampiezza di Veneziano e le sue generalizzazioni descrivessero in realtà un fenomeno del tutto nuovo: gli urti di stringhe.
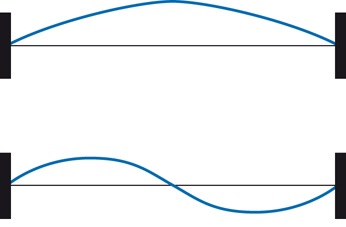
Le stringhe, o corde, si presentano in due forme topologicamente diverse ‒ chiuse e aperte ‒ e le infinite singolarità delle ampiezze di Veneziano e Shapiro-Virasoro sono una manifestazione degli infiniti tipi di eccitazioni per esse possibili. Una corda vibrante ideale, infatti, può essere descritta come un'infinità di oscillatori tra loro accoppiati e, conseguentemente, può vibrare su un'infinità di toni puri o modi normali; le frequenze caratteristiche wn sono associate alle masse mn∼wn di infinite particelle che corrispondono a tali modi normali. Le corde, chiuse o aperte, sono caratterizzate da una scala di lunghezza ℓs e appaiono essenzialmente puntiformi a distanze r≫ℓs. In modo analogo, il principio di indeterminazione della meccanica quantistica collega queste scale di distanza a energie E≪ℏc/ℓs, alle quali soltanto le particelle più leggere associate a una corda sono efficaci nei processi d'urto. In altri termini, le differenze tra una teoria di corde e una corrispondente teoria di particelle per i primi toni puri (la teoria effettiva di bassa energia) si manifestano soltanto a distanze r≤ℓs e, quindi, solamente a energie sufficientemente elevate.
Problemi con le applicazioni alla fisica adronica
L'analogia con le corde vibranti è, in realtà, parziale. La corda nella fig. 3 infatti ha soltanto toni puri di frequenze wn>0, ai quali corrisponderebbero particelle di masse mn>0 in grado di trasmettere forze avvertibili unicamente a distanze inferiori alle corrispondenti lunghezze Compton ℏ/mnc. Nei primi anni Settanta del secolo scorso si comprese che la teoria delle stringhe, invece, descrive inevitabilmente anche particelle di massa nulla, in grado, come i fotoni, di trasmettere forze a lungo raggio. Si trattava di un problema spinoso relativamente alle interazioni forti, che sono a corto raggio e svaniscono a distanze r∼10−15 m. Fatta eccezione per questa difficoltà, i modelli duali sembravano applicarsi in modo naturale agli adroni, i quali comprendono il protone, il neutrone e moltissime altre particelle instabili che, soggette alle interazioni forti, presentano una sorprendente regolarità nella distribuzione delle masse e degli spin. Nel piano (massa)2-spin, gli adroni si dispongono su traiettorie di Regge rettilinee che si prestano a una descrizione in termini di eccitazioni di stringhe con ℓs∼10−15 m, distanza che corrisponde, per le masse, a una scala di centinaia di MeV/c2 (o, equivalentemente, a una scala di centinaia di MeV per le energie di riposo). Ma questa scelta aveva una conseguenza inattesa: la formula di Veneziano e le sue generalizzazioni predicevano infatti un rapidissimo decremento delle sezioni d'urto con l'energia, tanto che esse sarebbero dovute svanire già a pochi GeV. In altri termini, la teoria sembrava indicare la scomparsa delle interazioni adroniche a energie di poco superiori all'energia di riposo del protone, ovvero a scale di distanza di poco inferiori a 10−16 m.
Questo risultato era però in completo disaccordo con i dati che i grandi acceleratori avevano fornito a partire dalla fine degli anni Sessanta: gli urti con elettroni evidenziavano infatti la presenza di oggetti puntiformi nel protone, mentre le corrispondenti sezioni d'urto non erano affatto rapidamente decrescenti con l'energia. I componenti puntiformi furono presto identificati con i quark, la cui esistenza era stata ipotizzata negli anni Sessanta da Murray Gell-Mann e George Zweig per riproporre, nell'ambito degli adroni, l'analogo del ruolo svolto dagli elettroni per la tavola di Mendeleev delle specie atomiche: per la prima volta i quark trovavano un ruolo dinamico in esperimenti d'urto. Un altro motivo di imbarazzo si presentò quando un'analisi più dettagliata dei diagrammi di stringa, dovuta a Claud Lovelace, rivelò che perché la teoria fosse coerente erano richieste venticinque dimensioni spaziali, in luogo delle tre dell'esperienza quotidiana. Infine, si comprese ben presto che la particella coinvolta nel processo d'urto di Veneziano ha una massa descritta da un numero immaginario. Particelle di questo tipo prendono il nome di tachioni e sono considerate un sintomo dell'instabilità del sistema che le descrive, proprio come le frequenze immaginarie indicano, negli ordinari sistemi macroscopici, l'instabilità di una configurazione di equilibrio. Tutto questo, unitamente al progresso sostanziale nella formulazione del Modello Standard delle interazioni elettrodeboli e forti delle particelle note, contribuì a distogliere per diversi anni l'attenzione della maggior parte dei fisici da questa teoria misteriosa e complessa, apparentemente incapace di rivestire un ruolo adeguato nella descrizione della natura.
Reinterpretazione come teoria della gravità
Esistono fondati motivi per ritenere che il Modello Standard non sia una teoria completa; tra questi, l'apparente incompatibilità delle sue equazioni con la relatività generale, che descrive in modo mirabile il Sistema solare, le stelle e le galassie che compongono l'Universo visibile e rappresenta la base tecnica e concettuale per la comprensione dell'evoluzione cosmologica. Tali difficoltà possono essere intuite confrontando tra loro l'intensità della forza coulombiana tra due particelle in quiete di massa m con cariche elettriche ±e,
[2] formula
dove −e è la carica dell'elettrone, e quella dell'attrazione newtoniana,
[3] formula
dove GN è la costante di gravitazione universale pari a 6,67×10−11 Nm2kg−2. L'analogia formale tra queste due espressioni, la seconda delle quali può ottenersi dalla prima per mezzo della sostituzione
[4] formula
riflette una profonda, seppur parziale, analogia tra i due tipi di interazioni. Entrambe possono essere infatti associate allo scambio di bosoni di massa nulla in grado di trasmettere forze a lungo raggio: il fotone e il gravitone, di spin, rispettivamente, uno e due. Si noti però che, mentre le proprietà sia ondulatorie sia corpuscolari della luce sono state evidenziate da tempo, non esiste ancora una prova sperimentale diretta dell'esistenza delle onde gravitazionali o dei gravitoni, anche se è possibile imputare questa lacuna all'estrema debolezza della forza gravitazionale in condizioni ordinarie.
L'intensità delle interazioni elettromagnetiche tra particelle elementari è determinata dalla costante di struttura fine α=e2/(4πε0ℏc)≃1/137; l'analogia tra i due tipi di forze, unitamente alla sostanziale equivalenza relativistica tra massa ed energia, suggerisce che l'intensità delle interazioni gravitazionali sia determinata da una corrispondente funzione di struttura fine
[5] formula
che cresce quadraticamente con l'energia. Alle scale di energia tipiche della fisica atomica, le forze gravitazionali in gioco (inferiori a quelle coulombiane di un fattore 10−40) sono assolutamente irrilevanti, ma divengono addirittura dominanti per energie superiori all'energia di Planck
[6] formula
o, equivalentemente, a distanze inferiori alla lunghezza di Planck
[7] formula.
Anche se ℓPl è inferiore di molti ordini di grandezza rispetto alle scale di distanza attualmente esplorabili, il comportamento della funzione αG(E) ha conseguenze drammatiche sui diagrammi con loop. I processi intermedi possono infatti coinvolgere gravitoni di energia arbitrariamente elevata (per es. nel loop della fig. 2), rendendo di fatto vano il calcolo delle corrispondenti sezioni d'urto. Ma se ℓs∼10−35 m, la teoria delle stringhe è in grado di offrire a questo problema una soluzione inattesa, proposta nel 1974 da Joel Scherk, John H. Schwarz e Tamiaki Yoneya. Le ampiezze di Veneziano e Shapiro-Virasoro avevano ben presto rivelato che le eccitazioni delle stringhe aperte includono almeno un fotone e, in generale, campi di Yang-Mills, mentre quelle delle stringhe chiuse includono sempre un gravitone, le cui mutue interazioni a distanze r≫ℓs sono descritte appunto dalla teoria di Yang-Mills e dalla relatività generale.
Scherk, Schwarz e Yoneya proposero quindi di riconsiderare i modelli duali non come modelli degli adroni ma come base di una teoria della gravità e delle altre forze fondamentali che fosse in grado di eludere i problemi derivanti dalla relatività generale ad altissime energie. La loro efficacia in questo contesto si può intuire notando che soltanto piccole frazioni delle stringhe partecipano attivamente agli urti ad alte energie, dando luogo a un'effettiva riduzione di αG(E): la sola energia rilevante è di fatto la frazione di E che il principio di indeterminazione associa alla regione di interazione, e quindi vale la relazione
[8] formula.
In questo modo, ad alte energie la gravità si comporta come le interazioni elettromagnetiche, la cui intensità è determinata dalla costante di struttura fine, in quanto la crescita di αG(E) con l'energia si arresta alla scala di Planck.
Nella seconda metà degli anni Settanta, tra i pochi fisici rimasti a studiarne le proprietà, era pertanto diffusa la convinzione che la teoria delle stringhe potesse garantire una descrizione coerente di tutte le interazioni fondamentali delle particelle elementari. Il legame proposto tra la teoria delle stringhe e la gravità consentiva il ricorso a un meccanismo di compattificazione analogo a quello proposto da Theodor F.E. Kaluza e Oskar B. Klein negli anni Venti, che, nell'ambito della relatività generale, consente di mettere in relazione l'Universo con ulteriori dimensioni microscopiche. La loro esistenza non può essere rilevata sperimentalmente con particelle di energie troppo basse: le onde associate a queste ultime non potrebbero penetrarvi, così come le onde radio non riescono a penetrare in una galleria la cui sezione sia di dimensioni inferiori alla loro lunghezza d'onda.
Supergravità e superstringhe
Le particelle elementari comprendono vari fermioni: le tre generazioni di quark e leptoni presenti nel Modello Standard. Non deve quindi sorprendere che si sia resa presto necessaria un'estensione del modello di Veneziano e della corrispondente stringa bosonica, che includesse nella descrizione le particelle fermioniche. Tale stringa fermionica (o NSR), introdotta nel 1970 da André Neveu, Pierre Ramond e Schwarz, richiede un Universo con nove dimensioni spaziali e la sua formulazione matematica presentò per diversi anni una caratteristica piuttosto bizzarra, in quanto sembrava prevedere che alcune particelle violassero il principio di esclusione di Pauli. Questa difficoltà fu superata per la prima volta nel 1977 da Ferdinando Gliozzi, Joel Scherk e David I. Olive, che restrinsero lo spazio degli stati ammissibili della stringa NSR in modo tale che tutti i suoi fermioni fossero soggetti al principio di Pauli. Questa proiezione, detta GSO dalle iniziali dei tre studiosi, è uno dei più importanti contributi alla teoria delle stringhe; essa era stata motivata in origine dal tentativo di evidenziare una supersimmetria, stabilendo così una corrispondenza tra le particelle bosoniche e fermioniche del modello NSR ed eliminando allo stesso tempo tutti i possibili tachioni. La supersimmetria è una simmetria in grado di collegare tra loro particelle bosoniche e particelle fermioniche; nelle sue realizzazioni più semplici implica l'esistenza, apparentemente non realizzata in natura, di bosoni e fermioni di uguale massa. Per esempio, il Modello Standard non possiede questa simmetria perché contiene molte particelle fermioniche e, oltre ai dodici bosoni di gauge di SU(2)×U(1)×SU(3), soltanto una particella bosonica, peraltro non ancora osservata: il bosone di Higgs. Nel 1974 Julius Wess e Bruno Zumino proposero il primo modello concreto con supersimmetria e nel 1976 Sergio Ferrara, Daniel Z. Freedman e Peter van Nieuwenhuizen formularono un'elegante estensione della relatività generale, nota come supergravità. In questo caso la supersimmetria determina anche le interazioni del gravitone con un'altra particella di spin 3/2, il gravitino.
La stessa proiezione GSO era nata in realtà da un tentativo di collegare la stringa NSR a un modello simile definito in dieci dimensioni (una temporale e nove spaziali), noto come supergravità di tipo I. Al risultato così ottenuto, detto comunemente superstringa di tipo I e caratterizzato dalla presenza simultanea di stringhe aperte e chiuse, si aggiunsero negli anni successivi altri due modelli, definiti in dieci dimensioni: le superstringhe IIA e IIB, contenenti soltanto stringhe chiuse e collegate a corrispondenti supergravità, dette anch'esse IIA e IIB. La supersimmetria garantisce la stabilità di tali superstringhe, tutte prive di tachioni. Una supergravità in undici dimensioni (il tempo e le dieci spaziali) in grado di generare in qualche modo tutte le altre fu proposta infine nel 1978 da Eugene Cremmer, Bernard L. Julia e Scherk. La sua esistenza apparve per molti anni inspiegabile perché, a differenza dei tre modelli I, IIA e IIB in dieci dimensioni che descrivono eccitazioni di bassa energia di corrispondenti superstringhe, la struttura di questa teoria indicava chiaramente l'assenza di un legame diretto di questo tipo.
Meccanismo di Green-Schwarz e stringa eterotica
La corretta definizione di una teoria risiede in un certo numero di condizioni di coerenza, legate alla richiesta che le simmetrie responsabili delle interazioni non diano luogo ad anomalie e siano perciò compatibili con la meccanica quantistica. Verso la metà degli anni Ottanta del secolo scorso era ormai chiaro che sia la supergravità IIA sia la stringa corrispondente non presentano questo tipo di problema e Luis Alvarez-Gaumé ed Edward Witten dimostrarono che lo stesso avviene per la supergravità IIB e per la superstringa corrispondente. Poiché incompatibilità di questo tipo non possono presentarsi direttamente in un numero dispari di dimensioni, anche la supergravità in undici dimensioni ne è chiaramente esente, ma bisognava ancora considerare la teoria di tipo I, che, anzi, a prima vista sembrava soffrirne. Nel 1984 Michael B. Green e Schwarz, in uno dei più importanti contributi alla teoria delle stringhe, mostrarono invece che la superstringa di tipo I è sorprendentemente priva di anomalie grazie a un meccanismo del tutto nuovo per la loro cancellazione. Ciò provocò un'esplosione di interesse, tanto che ancora oggi alcuni enfaticamente associano l'anno 1984 alla prima rivoluzione delle superstringhe.
In realtà, il risultato da essi ottenuto selezionava due possibili supergravità di tipo I, con campi di Yang-Mills associati a matrici corrispondenti ai gruppi SO(32) e E8×E8 (E8 è il più grande dei gruppi eccezionali della classificazione di Élie Cartan), ma Neil Marcus e chi scrive avevano già mostrato da tempo l'impossibilità di associare questi gruppi eccezionali direttamente a stringhe aperte e quindi alla superstringa di tipo I. La stringa eterotica, proposta nei mesi successivi da David J. Gross, Jeffrey A. Harvey, Emil Martinec e Ryan Rohm, consentì di realizzare entrambe le possibilità utilizzando solamente stringhe chiuse. Si chiamerà per brevità HO la stringa eterotica con gruppo di gauge SO(32) e HE quella con gruppo di gauge E8×E8. La superstringa di tipo I, in un certo senso la più ricca e profonda perché l'unica a contenere stringhe sia chiuse sia aperte, fu quindi abbandonata dai più. Per diversi anni intensi sforzi furono dedicati al tentativo di collegare al Modello Standard la stringa eterotica HE, che al tempo appariva particolarmente promettente.
Nell'interpretare la teoria delle stringhe come base per unificare la gravità con le altre interazioni fondamentali, è necessario anzitutto collegarla alla nostra percezione di un Universo con tre dimensioni spaziali e questo è possibile grazie al meccanismo di Kaluza e Klein. L'Universo potrebbe infatti contenere alcune dimensioni che si sono cristallizzate su scale microscopiche nei primi istanti dell'espansione cosmologica, ma sia la relatività generale sia la teoria delle stringhe non sono apparentemente in grado di fornirci ragioni sul perché questo sia avvenuto. In relatività generale, infatti, non esiste un concetto generale di energia associato allo spazio-tempo che consenta di ordinare diverse scelte non equivalenti, per esempio con numeri differenti di dimensioni spaziali macroscopiche; l'attuale comprensione della teoria delle stringhe non consente di superare questa cruciale difficoltà dei meccanismi di compattificazione. Dare un senso di necessità alla scelta di un Universo con tre dimensioni spaziali macroscopiche è forse la sfida più importante che dovrà essere affrontata nei prossimi anni, ma è comunque possibile esplorarne le conseguenze nella teoria delle stringhe, chiarendo al contempo le sue potenzialità.
Queste ricerche hanno seguito due linee ben distinte, collegate rispettivamente alla supergravità di bassa energia e alla teoria completa. Nel primo caso, Phillip Candelas, Gary T. Horowitz, Andrew Strominger e Witten hanno mostrato già nel 1985 che ampie classi di soluzioni delle equazioni della supergravità, note come spazi di Calabi-Yau, producono universi con tre dimensioni spaziali macroscopiche che esibiscono diverse caratteristiche del Modello Standard. Caratteristiche simili sono poi emerse anche da soluzioni complete della teoria delle stringhe, disponibili però soltanto per spazi interni particolarmente semplici (orbifolds) introdotti in questo contesto da Lance Dixon, Jeffrey A. Harvey, Cumrun Vafa e Witten. Lo sviluppo di questi metodi ha permesso di esplorare con successo ampie classi di modelli con tre dimensioni spaziali macroscopiche, grazie principalmente ai contributi di Kumar S. Narain, Ignatios Antoniadis, Costas Bachas, Costas Kounnas, Hikaru Kawai, David Lewellen, Henry S.-H. Tye, Wolfgang Lerche, Dieter Lust e Bert Schellekens. In tal modo è stato anche possibile giungere ad alcune conclusioni generali: nelle stringhe eterotiche HE e HO, la descrizione della gravità con il corretto valore di GN richiede inevitabilmente che ℓs∼ℓPl∼10−35 m, rendendo le eccitazioni di stringa inaccessibili. Gli attuali acceleratori esplorano infatti distanze d∼10−18 m e non è possibile concepire alcuna tecnologia che fornisca informazioni dirette su scale dell'ordine della lunghezza di Planck.
Brane e orientifolds
Il comportamento delle teorie con stringhe aperte, che è andato delineandosi a partire dalla fine degli anni Ottanta del Novecento, ha suscitato notevoli sorprese, suggerendo anche scenari nei quali alcune conseguenze della teoria potrebbero manifestarsi già nella prossima generazione di acceleratori. Tra la fine degli anni Ottanta e l'inizio degli anni Novanta, lo studio della supergravità aveva già evidenziato che i toni puri delle stringhe non esauriscono le particelle corrispondenti. Questo tipo di situazione si realizza anche in altre teorie ben più semplici, nelle quali le usuali particelle sono accompagnate da altre molto massive, dette solitoni, sorprendentemente stabili perché dotate di cariche che, conservandosi, ne impediscono la disintegrazione. Un esempio notevole è il monopolo di 't Hooft-Polyakov, una particella molto massiva dotata di carica magnetica presente in alcune estensioni del Modello Standard. Anche se a tutt'oggi nessun monopolo magnetico è stato osservato, da anni ci si dedica con tenacia a ricerche di questo tipo in diversi laboratori.
I vari modelli della teoria delle stringhe ammettono diversi tipi di solitoni, che sono oggetti estesi: non semplicemente stringhe, ma piuttosto membrane generalizzate, con vari numeri p di dimensioni spaziali, dette comunemente p-brane. Il loro studio ha coinvolto molti ricercatori, tra i quali Eric Bergshoeff, Curtis Callan, Michael J. Duff, Harvey, Chris Pope, Soo-Joung Rey, Ergin Sezgin, Strominger e Paul K. Townsend. Uno sviluppo collegato, anche se ottenuto con metodi diversi, ha evidenziato la natura del modello di tipo I con stringhe aperte e chiuse, che può essere visto come il risultato di un anomalo meccanismo di Kaluza e Klein operante nel modello IIB di sole stringhe chiuse. Questa costruzione, detta orientifold, proposta nel 1987 da chi scrive e analizzata nel decennio successivo presso l'Università di Roma Tor Vergata anche da Massimo Bianchi, Gianfranco Pradisi, Yassen S. Stanev e Carlo Angelantonj, unifica le teorie I e IIB riducendo a quattro i tipi di superstringhe. Verso la metà degli anni Novanta, Joseph Polchinski, traendo spunto da precedenti contributi di Jin Dai, Robert G. Leigh e Green e procedendo in modo indipendente, ha associato gli estremi delle stringhe aperte a ulteriori tipi di solitoni, detti Dp-brane, sui quali essi sono di fatto confinati, e ha anche identificato le cariche che garantiscono la loro stabilità. Un osservatore che vivesse in una generica p-brana percepirebbe la presenza di particelle di spin zero associate alle sue vibrazioni nello spazio ambiente, ma le Dp-brane possono dar luogo a una simile percezione di fotoni, bosoni W e gluoni. In realtà, un'opportuna collezione di Dp-brane con p≥3 potrebbe ospitare tutti i tipi di particelle del Modello standard ed essere essa stessa l'intero Universo accessibile alle interazioni deboli, forti ed elettromagnetiche.
In scenari di questo tipo, noti come brane worlds, la costante di Newton GN sarebbe il risultato di una media sulle ulteriori dimensioni accessibili alla sola forza di gravità. Non è possibile escludere che queste ulteriori dimensioni siano sorprendentemente grandi, perché una serie di difficoltà tecniche rende impossibile, allo stato attuale, esplorare la forza di gravità a distanze inferiori a 10−4 m. In altri termini, come proposto alla fine degli anni Novanta da Antoniadis, Nima A. Hamed, Savas Dimopoulos e Georgi Dvali, non soltanto l'Universo potrebbe essere una collezione di brane che fluttua in un bagno di gravità, ma alcune dimensioni spaziali esterne alle brane dove sono confinati i campi di gauge e la materia, direttamente accessibili soltanto alla gravità, potrebbero anche essere macroscopiche. In analogia con le onde radio cui ci si è riferiti in precedenza, in questo scenario la galleria delle dimensioni aggiuntive sarebbe ampia e capiente, ma i nostri generatori non sarebbero in grado di introdurvi onde a causa dell'estrema debolezza della forza gravitazionale tra particelle elementari per energie inferiori alla scala di Planck. Un semplice argomento di analisi dimensionale suggerito dalla relatività generale mostra che, in questi scenari, n ulteriori dimensioni circolari di raggio R potrebbero occultare una scala fondamentale MPl,n in 3+n dimensioni spaziali di 1000 GeV soltanto, evidenziando invece una scala di Planck effettiva MPl∼1019 GeV già se
[9] formula
una possibilità non esclusa se n≥2, vale a dire se fossero presenti almeno due ulteriori dimensioni macroscopiche. La prossima generazione di acceleratori sarà in grado di fornire utili indicazioni in tal senso, ma è opportuno ricordare che l'attuale comprensione della teoria delle stringhe non esclude altri scenari meno interessanti dal punto di vista sperimentale, con valori più alti di MPl,n, nei quali questi effetti sarebbero fuori dalla portata dei prossimi esperimenti.
Dualità e M teoria
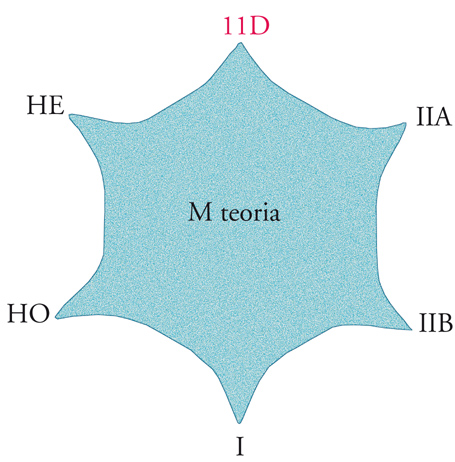
L'esistenza dei vari solitoni e delle loro eccitazioni, lungi dall'essere una complicazione, semplifica la teoria delle stringhe perché rende le cinque superstringhe IIA, IIB, I, HE e HO tra loro equivalenti, compensando di fatto le differenze esistenti tra i loro toni puri. L'unificazione di questi modelli è un risultato di valore concettuale straordinario, ottenuto verso la metà degli anni Novanta del Novecento con contributi sostanziali di vari autori, tra i quali Duff, Anna Maria Font, Lust, Luis E. Ibáñez, Fernando Quevedo, Townsend e Chris M. Hull, ma dovuto principalmente alla profonda sintesi operata da Witten. Al momento non ci sono argomenti ugualmente convincenti che colleghino le cinque superstringhe con la stringa bosonica, sebbene da tempo esistano interessanti suggerimenti in tal senso, e quindi il procedimento di unificazione non può considerarsi del tutto concluso.
La teoria delle stringhe finì comunque per stupire nuovamente gli addetti ai lavori quando Townsend e Witten riuscirono a collegare i cinque modelli in dieci dimensioni, ormai non equivalenti, alla supergravità in undici dimensioni. A fronte di questi sviluppi, si è dunque giunti a una situazione in qualche modo paradossale. Da una parte, l'equivalenza sostanziale tra le cinque superstringhe giustifica la convinzione di aver identificato indirettamente una teoria unica, detta comunemente M teoria, in grado di fornire una descrizione esauriente delle interazioni fondamentali sulla base di pochi principî essenziali. Dall'altra parte, tali equivalenze inducono almeno a una certa cautela, in quanto il vertice 11D nella fig. 4 non corrisponde a un modello di stringhe. La situazione ricorda quella vissuta dai padri della fisica moderna all'inizio del secolo scorso, quando le tecniche di calcolo disponibili consentivano già di descrivere accuratamente gli spettri atomici ma mancavano ancora i principî della meccanica quantistica. In altri termini, è possibile intravedere diversi elementi molto incoraggianti, ma ogni esperto del campo incontrerebbe oggi serie difficoltà nel definire i principî alla base della teoria delle stringhe.
Entropia dei buchi neri
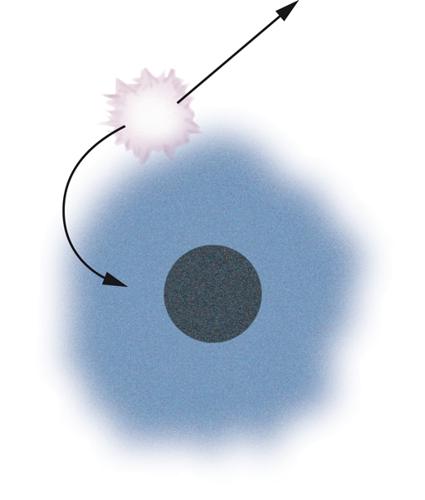
È stato comunque possibile esplorare alcune predizioni della teoria delle stringhe in altri ambiti, ottenendo risultati per molti versi inattesi. Una situazione di questo tipo è legata al problema dell'entropia dei buchi neri. Queste soluzioni classiche della relatività generale, simili per certi versi ai solitoni già descritti, sono caratterizzate da campi gravitazionali tanto intensi da isolare il loro interno dallo spazio circostante. Tutto cade in un buco nero, anche la luce, e quindi nessun tipo di segnale può uscire dal suo interno attraverso l'orizzonte che lo delimita. In realtà la meccanica quantistica modifica questo stato di cose, perché le fluttuazioni introdotte dal principio di indeterminazione consentono la dispersione attraverso l'orizzonte di uno spettro termico di radiazione, predetto nel 1974 da Stephen Hawking, e quindi anche l'evaporazione dei buchi neri per effetti quantistici (fig. 5). Questa emissione spontanea associa a un buco nero di massa M la temperatura di Hawking TH ∼1/M, e quindi, come inizialmente proposto da Jacob Bekenstein, un'entropia.
L'entropia è in generale una misura del disordine di un sistema: per esempio, in un gas essa dà conto del fatto che, anche fissando le grandezze macroscopiche rilevanti, ossia pressione, volume e temperatura, i moti microscopici delle molecole che contribuiscono a determinarle restano incontrollabili. In accordo con la formula di Boltzmann
[10] S = kB logW
dove kB = 1,38∙10−23 J/K è la costante di Boltzmann, l'entropia S misura quindi il numero W di microstati corrispondenti a un dato macrostato. Nella fisica dei buchi neri il problema consisteva appunto nell'identificare quali fossero i microstati responsabili dell'entropia, sulla cui natura la relatività generale non fornisce alcuna indicazione. Seguendo i contributi di Ashoke Sen, Vafa, Strominger e altri, per una classe di buchi neri resi particolarmente semplici dalla supersimmetria è stato possibile ottenere un risultato di grande valenza concettuale, identificando questi microstati con opportune eccitazioni di stringa nell'intorno dell'orizzonte e collegando quindi l'entropia di Bekenstein-Hawking ai principî della meccanica statistica.
La corrispondenza AdS/CFT
L'introduzione della cromodinamica quantistica (QCD, quantum chromodynamics) ha consentito di descrivere in modo molto efficiente gli urti tra quark ad alte energie, ma ha posto il problema di giustificare teoricamente il loro confinamento all'interno degli adroni. Anche se un'analisi quantitativa presenta enormi difficoltà, il fenomeno appare naturale (figg. 6A e 6B) se i quark sono legati tra loro da fasci di linee di forza compresse dalle interazioni forti della QCD in corde di spessore finito Δ≤10−15 m. Si è quindi tentato a lungo di derivare dalla QCD una teoria effettiva di queste stringhe 'spesse', ma un preciso legame tra le teorie di gauge e le stringhe è apparso a lungo elusivo, anche se nel limite di 't Hooft, ottenuto estendendo i tre colori della QCD a un numero N arbitrariamente grande, la teoria di Yang-Mills esibisce alcune chiare similitudini qualitative con le stringhe.
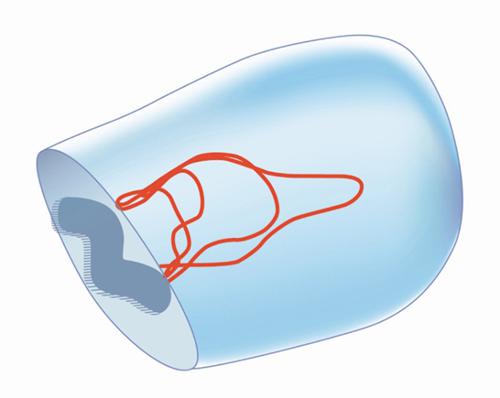
Nel 1997 Juan M. Maldacena ha proposto una sorprendente corrispondenza quantitativa di questo tipo tra la superstringa IIB in cinque dimensioni, su uno spazio-tempo curvo (AdS5×S5, il prodotto diretto di uno spazio di anti-de Sitter in 5 dimensioni e di una sfera in 5 dimensioni), e una teoria di Yang-Mills sul suo bordo, identificabile con l'usuale spazio di Minkowski in quattro dimensioni. Il legame risultante tra gravità e teorie di gauge riflette una profonda corrispondenza tra le stringhe chiuse, le cui eccitazioni di bassa energia includono i gravitoni, e le stringhe aperte, che hanno un simile legame con la teoria di Yang-Mills; il problema è in realtà molto complesso e la corrispondenza è pienamente sotto controllo solo in pochi casi di teorie con supersimmetria, che peraltro non esibiscono il fenomeno del confinamento. La corrispondenza è particolarmente semplice per la n=4 Yang-Mills, un esempio notevole di teoria supersimmetrica con invarianza conforme (CFT). È comunque possibile associarle un'immagine suggestiva e sostanzialmente corretta: le fluttuazioni di stringhe infinitamente sottili che dal bordo di AdS5 penetrano al suo interno fanno sì che, per un osservatore in grado di rilevare solo l'ombra che esse lasciano in media nel nostro spazio-tempo, queste sembrino possedere un effettivo spessore (fig. 7). In tal modo le corde di spessore finito della QCD possono essere collegate, seppure in modo indiretto, a quelle idealmente sottili della teoria delle stringhe, e la supergravità può fornire importanti indicazioni sul comportamento delle interazioni di Yang-Mills.
In conclusione, la teoria delle stringhe elimina il problema ultravioletto della relatività generale, diluendo l'energia delle particelle su oggetti estesi; le sue diverse manifestazioni sono riconducibili a un unico principio, detto M teoria, che però non è direttamente connessa alle sole stringhe ma piuttosto a diversi tipi di p-brane. Esiste quindi una notevole fiducia nelle prospettive di queste costruzioni, unitamente alla convinzione che non si sia ancora giunti a definirne pienamente i principî, il che rende la ricerca ancora più interessante. È bene mettere in evidenza che a tutt'oggi non esistono dati sperimentali che rendano imperativo il ricorso alla teoria delle stringhe, che resta pertanto un'elegante quanto ponderosa speculazione teorica. Le cause di questa situazione vanno ricercate in parte nella difficoltà di effettuare esperimenti convenzionali nella fisica delle particelle elementari (per es., per motivi tecnici legati alla costruzione di un nuovo acceleratore, sei o sette anni almeno separeranno gli ultimi esperimenti effettuati al CERN da quelli della prossima generazione) e in parte nelle difficoltà di carattere matematico che si incontrano nell'analizzare la teoria delle stringhe. Per esempio, gli sviluppi più promettenti sono basati sulla supersimmetria, che semplifica notevolmente le equazioni risultanti, eliminando però alcune caratteristiche che si presentano inevitabilmente in un confronto quantitativo con il Modello Standard.
In ogni caso, la ricchezza dei concetti coinvolti e il loro legame con profondi aspetti della matematica contemporanea rendono lo studio della teoria delle stringhe una delle più affascinanti sfide intellettuali che la fisica si sia trovata ad affrontare e che, indirettamente, ha già contribuito in modo sostanziale a una comprensione più profonda dei concetti alla base della teoria quantistica dei campi e dello stesso Modello Standard. È ragionevole prevedere che nei prossimi anni ricerche legate alla natura del vuoto, e in particolare ai criteri di scelta delle dimensioni aggiuntive, avranno un ruolo preminente nella teoria delle stringhe. In generale, le fluttuazioni quantistiche introdotte dal principio di indeterminazione conferiscono al vuoto un ruolo importante in meccanica quantistica; problemi di questo tipo si presentano anche nel Modello Standard, dove un condensato bosonico responsabile della natura a corto raggio delle interazioni deboli implica l'esistenza di una particella di spin zero e massa m∼120 GeV, il bosone di Higgs, l'anello mancante nella verifica delle predizioni teoriche.
Questo meccanismo di rottura spontanea di simmetria suggerisce la possibilità di comprendere in termini non troppo dissimili la natura delle eccitazioni massive delle stringhe, la cui scala caratteristica ℓs potrebbe anch'essa emergere da un opportuno condensato. Un altro problema ugualmente importante è legato alle energie di vuoto prodotte dalla formazione di condensati di questo tipo o dalla nucleazione di p-brane. Si tratta di fenomeni che ricordano in qualche modo la transizione liquido-vapore, ma in una teoria della gravità le energie risultanti curvano lo spazio-tempo, tipicamente in modo eccessivo in relazione alla dinamica cosmologica. Non è chiaro se e come la teoria delle stringhe potrà essere d'aiuto nella comprensione del problema della costante cosmologica, legato all'esiguità della curvatura media dell'Universo rilevata in cosmologia, e nemmeno, a un livello più strettamente tecnico, come essa potrà convivere con i meccanismi che la generano.
Bibliografia
Aharony 2000: Aharony, Ofor e altri, Large N field theories, string theory and gravity, "Physics reports", 323, 2000, pp. 183-386.
Alvarez 1989: Alvarez, Enrique, Quantum gravity. A pedagogical introduction to some recent results, "Review of modern physics", 61, 1989, pp. 561-604.
Angelantonj, Sagnotti 2002: Angelantonj, Carlo - Sagnotti, Augusto, Open strings, "Physics reports", 371, 2002, pp. 1-156.
Antoniadis 2001: Antoniadis, Ignatios, String and D-brane physics at low energy, CERN-TH/2001-065, 0023/IHP.
Bachas 1997: Bachas, Constantin P., Lectures on D-branes, in: High energy physics - theory, abstract, hep-th/9806199.
Coleman 1985: Coleman, Sidney, Aspects of symmetry, Cambridge, Cambridge University Press, 1985.
Dudas 2000: Dudas, Emilian, Theory and phenomenology of type I strings and M-theory, "Classical and quantum gravity", 17, 2000, pp. R41-R116.
Duff 1996: Duff, Michael J., M-theory (the theory formerly known as strings), "International journal of modern physics A", 11, 1996, pp. 5623-5642.
Green 1988: Green, Michael B. - Schwarz, John H. - Witten, Edward, Superstring theory, Cambridge, Cambridge University Press, 1988.
Greene 1999: Greene, Brian, The elegant universe, New York, Norton & Company, 1999.
Ibanez 2000: Ibanez, Luis E., The second string (phenomenology) revolution, "Classical and quantum gravity", 17, 2000, pp. 1117-1128.
Jacob 1974: Dual theory, edited by Maurice Jacob, Amsterdam-Oxford, North-Holland, 1974.
Johnson 2000: Johnson, Clifford, V., D-brane primer, in: High energy physics - theory, abstract, hep-th/007170.
Johnson 2002: Johnson, Clifford V., D-branes, Cambridge, Cambridge University Press, 2002.
Mandl, Shaw 1984: Mandl, Franz - Shaw, Graham, Quantum field theory, Chichester-New York, Wiley, 1984.
Olive 1996: Olive, David I., Exact electromagnetic duality, "Nuclear physics proceedings supplement", 45A, 1996, pp. 88-102; 46, 1996, pp. 1-15.
Polchinski 1996: Polchinski, Joseph - Chaudhuri, Shyamoli - Johnson, Clifford, Notes on D-branes, in: High energy physics - theory, abstract, hep-th/9602052.
Polchinski 1998: Polchinski, Joseph, String theory, Cambridge, Cambridge University Press, 1998.
Scherk 1975: Scherk, Joel, An introduction to the theory of dual models and strings, "Review of modern physics", 47, 1975, pp. 123-164.
Sen 1997: Sen, Ashoke, Unification of strings duality, "Nuclear physics proceedings supplement", 58, 1997, pp. 5-19.
Townsend 1997: Townsend, Paul K., Four lectures onM-theory, in: Proceedings of the 1996 ICTP summer school on high energy physics and cosmology, edited by Edi Gava e altri, Singapore-River Edge (N.J.), World Scientific, 1997.