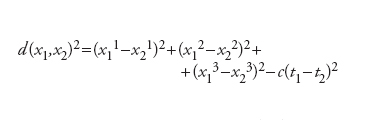invarianza di Lorentz
invarianza di Lorentz
Proprietà di certe quantità fisiche di non mutare (ovvero rimanere invarianti) per trasformazioni di Lorentz. Queste grandezze sono dette invarianti o scalari di Lorentz. Nella teoria della relatività ristretta l’invarianza di Lorentz è ottenuta formulando tutte le leggi fisiche in termini di scalari, vettori, tensori o spinori definiti sullo spazio di Minkowski. Quest’ultimo svolge in questo contesto il ruolo di spazio-tempo ed è dunque una varietà quadridimensionale (tre dimensioni spaziali più una temporale). Una trasformazione di Lorentz è allora una trasformazione affine che lasci invariata la distanza d(x1,x2) tra due eventi x1=(x11,x12, x13,t1) e x2=(x21,x22,x23,t2) nello spazio-tempo, distanza espressa dalla formula
dove c è la velocità della luce. Si noti che la quantità d(x1,x2)2 può anche assumere valori negativi: la metrica sullo spazio di Minkowski non è dunque definita positiva. Le trasformazioni di Lorentz formano un gruppo detto gruppo di Lorentz.
→ Astrofisica delle alte energie