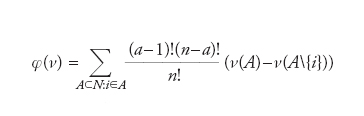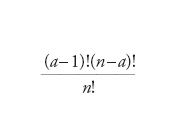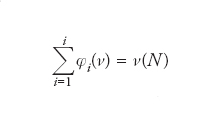indice di Shapley
indice di Shapley
Un gioco cooperativo a utilità trasferibile, in cui N={1,2,…,n} è l’insieme dei giocatori, è una funzione ν:P(N)→ℝ, tale che ν(∅)=0. Con P(N) si indica l’insieme dei sottoinsiemi di N, che rappresentano tutte le possibili coalizioni fra giocatori. La funzione ν invece, detta funzione caratteristica del gioco, indica il guadagno associato alle coalizioni (o anche un costo associato alle coalizioni). La teoria cooperativa è interessata a stabilire quanto debba essere assegnato a ogni singolo giocatore, sulla base delle informazioni contenute nella funzione ν. Si chiama soluzione del gioco cooperativo a N giocatori una funzione φ che mappa lo spazio dei giochi (che è isomorfo allo spazio euclideo a 2ν−1 dimensioni), nello spazio dei vettori n-dimensionali. Dire che φ(ν)=(x1,…,xν) significa che la soluzione assegna, nel gioco v, la quantità xι al giocatore i-esimo. La soluzione φ proposta da Shapley (detto anche indice di Shapley) è la seguente: indicando con φι la sua iesima componente abbiamo
dove a rappresenta il numero dei giocatori che formano la coalizione A. La quantità ν(A)−ν(A{i}) è il contributo marginale portato dal giocatore i alla coalizione A. L’indice di Shapley pesa i contributi marginali che il giocatore i porta a ogni coalizione in cui potrebbe entrare, con un coefficiente che ha una sua interpretazione probabilistica. Infatti la quantità
rappresenta la probabilità che il giocatore i entri a far parte della coalizione A se i giocatori si danno appuntamento in un certo posto, gli arrivi sono equiprobabili, e ogni giocatore si coalizza solo con i giocatori già presenti. L’indice di Shapley gode di notevoli proprietà. Tra queste, il fatto che assegna ai giocatori tutta la quantità disponibile ossia
non assegna nulla ai giocatori che non portano contributi alle coalizioni, assegna uguale utilità a giocatori che portano lo stesso contributo a tutte le coalizioni, e infine è una funzione lineare sullo spazio dei giochi, serve a caratterizzarlo completamente. Infatti è l’unica soluzione che gode delle proprietà precedenti sullo spazio dei giochi a utilità trasferibile. L’indice di Shapley non rappresenta soltanto un interessante concetto di soluzione, ma è particolarmente utile anche per valutare i rapporti di forza fra i giocatori in varie situazioni, come per es., gli azionisti in una società per azioni, o i partiti in un Parlamento, tutte situazioni modellizzabili come giochi cooperativi.