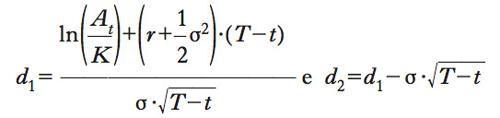Black-Scholes, formula di
Black-Scholes, formula di
Formula che consente di esprimere in modo sintetico il prezzo teorico di una ordinaria opzione di tipo europeo (➔ opzioni europee) su un’attività finanziaria, tipicamente un’azione, che non paga dividendi e il cui prezzo evolve nel tempo secondo un opportuno modello aleatorio.
La formula prende il nome dai due studiosi che la proposero (F. Black e M. Scholes, The pricing of options and corporate liabilities, «Journal of Political Economy», 1973, 81,3), ma fu indipendentemente ricavata anche da R. Merton (Theory of rational option pricing, «Bell Journal of Economics and Management Science», 1973, 4, 1). Questa primogenitura congiunta fruttò il premio Nobel 1997 per l’economia a Merton e a Scholes, ma non a Black, prematuramente scomparso. Considerata una pietra miliare della teoria della finanza, la formula ha avuto un formidabile impatto nella diffusione dei mercati dei derivati.
Bisogna premettere che un’opzione call (call option) dà al suo detentore il diritto, ma non l’obbligo, di comperare a un’epoca futura T il titolo (l’azione) sottostante pagando, non il prezzo corrente a quell’epoca, bensì un prezzo prefissato, detto prezzo di esercizio (o in gergo anglosassone strike, a indicare la fissità di tale posizione). La locuzione ‘prezzo di esercizio’ non va fraintesa; non si tratta di un prezzo di equilibrio di mercato ma di un parametro sostanzialmente esogeno, in quanto frutto di un libero accordo contrattuale tra le parti. Il prezzo di equilibrio è invece appunto il prezzo teorico dell’opzione. Nella formula di B.-S. esso viene espresso come differenza fra un opportuno aggiustamento del valore corrente del sottostante e il valore attuale del prezzo di esercizio, anch’esso aggiustato. Gli aggiustamenti si ottengono applicando coefficienti moltiplicativi ai rispettivi valori base. Indicando rispettivamente con Ct e At i valori correnti dell’opzione e del sottostante, con VK il valore attuale dello strike K e con N(d1) e N(d2) i rispettivi coefficienti moltiplicativi si ha: Ct=At‧N(d1)−VK‧N(d2). I coefficienti N(d) compresi fra 0 e 1 sono le probabilità che una distribuzione normale standard assuma determinazione inferiore a d. In dettaglio:
Nella formula compaiono 5 parametri (At, K, T−t, r, σ). I primi 3 sono contrattuali, gli altri sono il tasso istantaneo di interesse di mercato dell’attività non rischiosa e la volatilità del sottostante. L’ultimo parametro è anche l’unico non direttamente osservabile sul mercato e richiede procedure specifiche di stima. Le derivate parziali di Ct, rispetto ai parametri, dette greche dell’opzione (➔ opzioni, greche delle), esprimono la sensibilità del prezzo dell’opzione a piccole variazioni dei parametri stessi. La più importante, perché legata al rapporto di copertura, è la derivata parziale rispetto ad A, detta delta dell’opzione (➔ opzione). Il rapporto di copertura gioca un ruolo determinante nella derivazione della formula di Black-Scholes. Sfruttando sofisticati risultati di teoria della probabilità (➔ Ito, Kiyoshi), si può accertare che un portafoglio composto da una posizione lunga in delta unità del sottostante e una posizione corta in un’opzione call (➔ call option) è localmente non rischioso. In assenza di opportunità di arbitraggio, il rendimento locale di tale portafoglio deve pareggiare il rendimento locale dell’attività priva di rischio. Da questa eguaglianza consegue un’equazione differenziale alle derivate parziali, del secondo ordine, la cui soluzione, tenuto conto della condizione al contorno (valore a scadenza dell’opzione) è appunto la formula di Black-Scholes.