Crescita di strutture
Crescita di strutture
I concetti di legge di scala e di invarianza di scala rivestono un ruolo centrale nell'analisi di sistemi sempre più complessi, che si osservano nelle scienze fisiche ma anche in molti altri campi. A partire dalla struttura stessa dell'Universo a grande scala, passando per le complesse forme delle strutture biologiche, fino alle interazioni elementari tra i costituenti fondamentali della materia, tutti questi sistemi mostrano ben definite leggi di scala. Tali leggi descrivono come il sistema cambia sotto l'effetto di una trasformazione della scala delle lunghezze e questa proprietà rappresenta un elemento essenziale per la comprensione della complessità del sistema. Il metodo tradizionale della fisica è quello di considerare i sistemi più semplici e di studiarli in grande dettaglio. Questo approccio riduzionistico, così chiamato perché si focalizza sui 'mattoni' elementari che costituiscono la materia, si applica a un gran numero di situazioni e implica necessariamente l'esistenza di scale caratteristiche: la dimensione di un atomo, di una molecola o di un oggetto macroscopico.
Esistono però molti casi in cui la situazione è completamente diversa e la conoscenza dei singoli elementi non è sufficiente a caratterizzare la struttura nel suo insieme. Infatti, quando moltissimi elementi interagiscono tra loro in modo non lineare, possono dar luogo a strutture complesse le cui proprietà non possono essere ricondotte a quelle dei singoli costituenti. In questi casi è lecito pensare a una sorta di architettura della materia e della natura, che dipende in qualche modo dalle proprietà dei singoli elementi, ma poi si evolve in maniera indipendente da esse, dando luogo a strutture complesse con caratteristiche diverse da quelle dei singoli costituenti. Una di queste proprietà fondamentali è rappresentata appunto dalle leggi di scala, che caratterizzano il cambio delle proprietà del sistema al variare della scala. Per un sistema con una scala caratteristica, come un atomo, le leggi di scala non sono particolarmente interessanti.
In molti casi, però, osserviamo che le strutture naturali non sono affatto semplici, ma estremamente irregolari e questa irregolarità rappresenta una caratteristica intrinseca. In questi casi è necessario cambiare prospettiva rispetto ai metodi matematici tradizionali. Per questo motivo, nel considerare il problema della crescita di strutture, dovremo distinguere se si tratta di strutture regolari o con piccole irregolarità, come la crescita di un cristallo. Se invece consideriamo il problema di identificare i meccanismi microscopici che sono capaci di generare strutture complesse, allora è necessario considerare una prospettiva matematica e concettuale diversa. Anche i campi di applicazione possono essere i più svariati, perché, in generale, è possibile trovare strutture complesse in tutti quei sistemi costituiti da un gran numero di elementi che interagiscono in modo non lineare, e questo può spiegare l'intrinseca generalità di questa proprietà che ha cambiato il nostro modo di vedere sia i fenomeni naturali sia quelli sociali.
Modelli che generano strutture complesse
I modelli fisici che generano strutture complesse si possono dividere in due grandi categorie, quelli di equilibrio e quelli con una dinamica irreversibile. Nei modelli di equilibrio le strutture complesse hanno origine dalla competizione tra ordine e disordine, e avvengono soltanto in una particolare zona dei parametri del modello, la cosiddetta zona critica. I modelli irreversibili descrivono invece dei fenomeni di crescita in senso più appropriato e le strutture generate sono relativamente stabili rispetto ai parametri del modello. Di seguito elenchiamo i principali modelli.
Modello di Ising
Descrive spin con due posizioni (su o giù) definiti su un reticolo. L'interazione tra gli spin favorisce il loro allineamento, mentre la temperatura tende a rendere il sistema disordinato. Precisamente al punto critico, la competizione tra ordine e disordine genera dei cluster di spin correlati con proprietà di invarianza di scala. Questo modello fu introdotto nel lontano 1911 per il caso unidimensionale. Poi, negli anni Cinquanta, fu risolto esattamente il caso bidimensionale. Negli anni Settanta, il modello di Ising è diventato popolarissimo come metafora fondamentale di tutti i fenomeni critici e delle transizioni di fase continue (del secondo ordine). Tale modello ha avuto anche un ruolo essenziale nello sviluppo della teoria del gruppo di rinormalizzazione.
Percolazione
In questo modello i segmenti di un reticolo vengono occupati con un conduttore con probabilità p, altrimenti sono considerati isolanti. Per un valore critico di questa probabilità si sviluppa nel sistema un cluster conduttore infinito, con proprietà di invarianza di scala e definito da esponenti critici.
Caos deterministico
Questo modello consiste in una dinamica discretizzata non lineare che, in funzione di un parametro, si evolve da un attrattore semplice a situazioni più complesse, attraverso una serie di fenomeni di biforcazione. Per un valore critico di questo parametro l'attrattore ha proprietà frattali e viene definito 'strano'. Il modello del caos deterministico è spesso preso come esempio tipico dei fenomeni caotici.
Sistemi dinamici e turbolenti
Hanno origine principalmente dalle equazioni di Navier-Stokes e descrivono la turbolenza di un fluido. Le strutture complesse corrispondono alla distribuzione delle singolarità del campo delle velocità.
Sistemi vetrosi e vetri di spin
Questi sistemi sono intermedi tra quelli di equilibrio e di non equilibrio. Descrivono situazioni in cui c'è una competizione (frustrazione) tra diverse interazioni e sono caratterizzati dall'esistenza di moltissimi stati metastabili con energia libera simile. Questi stati mostrano proprietà complesse sia nello spazio fisico sia nello spazio delle fasi.
Sistemi granulari
Descrivono sistemi mesoscopici sottoposti a sollecitazioni che giocano un ruolo simile a quello della temperatura nei sistemi microscopici. Le loro proprietà possono essere simili a un fluido semplice o a un sistema vetroso, a seconda dei parametri considerati.
Percolazione invasiva
Considerato un reticolo, si assegna a ogni legame un valore fisso di resistenza (tra zero e uno). Il processo si evolve in modo irreversibile, invadendo il legame con resistenza minore tra quelli che sono intorno al suo perimetro. Sebbene la dinamica sia indubbiamente irreversibile, questo modello produce una struttura identica a quella della percolazione.
Modelli di polimeri e colloidi
Il più semplice modello di polimero è il random walk o cammino aleatorio. L'introduzione dell'effetto del volume escluso rende questo problema molto complesso, della stessa categoria del modello di Ising. Si possono avere situazioni di equilibrio o di crescita irreversibile a seconda della dinamica che si considera.
Modelli fisici di crescita frattale
I più interessanti e studiati sono quelli in cui la probabilità di crescita è lega-ta alla soluzione dell'equazione di Laplace intorno alla struttura. Permettono di descrivere un gran numero di strutture frattali.
Modelli di crescita di superfici irregolari
Se nei modelli laplaciani di crescita frattale si annulla l'effetto del laplaciano, si hanno strutture che sono internamente compatte. La superficie però rimane irregolare e mostra proprietà critiche e di scaling.
Modelli di tipo sandpile (pila di sabbia).
Questi modelli si focalizzano su come un sistema si può autoorganizzare in uno stato critico, in cui la risposta a una perturbazione può provocare valanghe di tutte le scale. Oltre a un'importanza concettuale, hanno diretta rilevanza per fenomeni come i terremoti e altri eventi estremi.
Network complessi
In questi modelli la complessità è nella struttura della topologia dei legami di un grafo. Anche qui le applicazioni sono moltissime e in svariati campi.
Modelli di instabilità gravitazionale
Questi modelli studiano le prime strutture che si sono formate nell'Universo a causa della gravità.
Dinamica fisica di crescita frattale e autoorganizzazione
Considerando che molte strutture in natura sono autosimili e complesse, è naturale domandarsi perché la natura produca questo tipo di strutture e quali sono i processi elementari alla base della loro formazione. Il primo modello fisico che genera spontaneamente strutture frattali è il DLA (Diffusion limited aggregation), formulato da Tom Witten e Len Sander nel 1981, che produce strutture complesse. Il modello è ispirato dall'osservazione che alcuni aggregati in fase gassosa (per es. il fumo) mostrano una struttura frattale. Si inizia con una particella fissa in un dato punto (centro) e si introduce a una determinata distanza R (abbastanza grande) una nuova particella, che esegue un moto browniano su un reticolo (diffusione). Quando questa particella arriva in un sito adiacente al centro, viene congelata in questa posizione e la struttura dell'aggregato si estende. Viene allora introdotta una nuova particella che raggiunge un altro sito adiacente al nuovo aggregato, e così via. L'iterazione di questo semplice algoritmo produce spontaneamente strutture di grande complessità con una dimensione frattale D=1,7 (per la crescita in un piano).
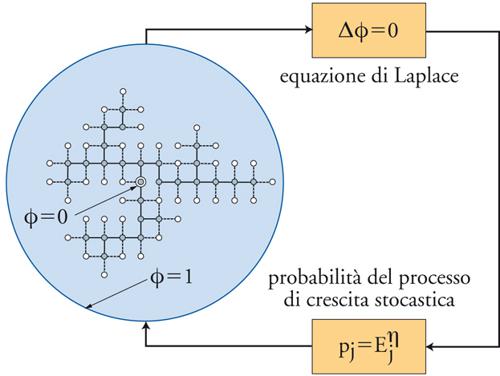
Successivamente, nel 1984, L. Niemeyer, L. Pietronero e H.J. Wiesmann introdussero il modello DBM (Dielectric breakdown model), ispirato dalle scariche nei gas (per es. i fulmini). Si assume che la struttura dove il collasso è già avvenuto sia equipotenziale. Partendo dall'equazione di Laplace, è possibile calcolare il campo elettrico locale per tutti i segmenti intorno alla struttura stessa. La probabilità di crescita per ogni segmento si assume proporzionale al campo elettrico locale. Un segmento viene selezionato in modo probabilistico e diventa parte della nuova struttura, come indicato nella fig. 3 . Il processo dinamico DBM, oltre a generare strutture di tipo DLA, ne chiarisce le proprietà matematiche in relazione alle equazioni alle derivate parziali. Questi frattali, detti frattali laplaciani, catturano le proprietà essenziali di vari fenomeni, come la deposizione elettrochimica, il breakdown dielettrico, le interfacce tra liquidi viscosi, la propagazione delle fratture e varie proprietà dei colloidi.
Un'interessante variante del DLA è il modello di aggregazione di tipo cluster-cluster, nel quale il processo di aggregazione inizia con molte particelle che seguono moti browniani e che possono aggregarsi in cluster di ogni dimensione, i quali si muovono anch'essi e si aggregano, e così via. Ogni cluster si rivela frattale con una dimensione inferiore rispetto al DLA. Inoltre, la distribuzione delle dimensioni dei cluster mostra un comportamento che segue una legge di potenza. Il modello cluster-cluster riesce a descrivere sistemi quali la polvere, il fumo e i colloidi.
Verso una comprensione teorica
I modelli discussi nel paragrafo precedente illustrano precise situazioni fisiche, che conducono alla generazione spontanea di strutture frattali in buon accordo con i risultati sperimentali. Tuttavia, per una comprensione teorica completa, è necessario identificare il ruolo dei diversi elementi dei modelli, la classificazione delle loro proprietà e possibilmente predire analiticamente il loro comportamento. Le differenze, rispetto alle transizioni di fase di equilibrio, sono che in questi modelli la dinamica è irreversibile e autoorganizzata. Un elemento cruciale è l'assenza di un principio ergodico, cioè l'impossibilità di sostituire una media sulla dinamica del sistema con una media sulle configurazioni statiche opportunamente pesate da un fattore tipo quello di Boltzmann. Quindi la fondamentale domanda di perché la natura produca strutture frattali, genera una problematica teorica di tipo nuovo, abbastanza diversa dal gruppo di rinormalizzazione che permette di spiegare i fenomeni critici usuali. Un tentativo di costruire una teoria fisica per i frattali autoorganizzati con dinamica irreversibile è costituito dal metodo della trasformazione a scala fissa. Questo approccio permette di capire l'origine dell'autoorganizzazione nella crescita frattale, in termini di un punto fisso attrattivo per la dinamica invariante di scala, e di calcolare analiticamente la dimensione frattale.
Strutture generate da instabilità gravitazionale
Un problema importante e molto studiato è quello delle strutture che si formano a causa dell'interazione gravitazionale. Questo problema è motivato dalle primissime strutture complesse che si sono formate nell'Universo e che oggi possiamo osservare in termini di galassie e ammassi di galassie. Queste strutture mostrano ben definite proprietà frattali, con dimensione D=2, che si estendono fino agli attuali limiti osservativi. Tali osservazioni appaiono in contraddizione con la notevole isotropia osservata nella radiazione di fondo. Il problema nasce dal fatto che, al tempo del disaccoppiamento tra radiazione e materia, cioè quando l'Universo era mille volte più piccolo, le proprietà della radiazione e della materia dovevano essere simili. Poiché la radiazione è rimasta grosso modo la stessa, l'idea è che le proprietà osservate oggi per la radiazione forniscono le condizioni iniziali per la distribuzione della materia al tempo del disaccoppiamento. In seguito, la materia, attraverso l'effetto della gravità, si sarebbe aggregata fino a formare le strutture frattali che oggi osserviamo.
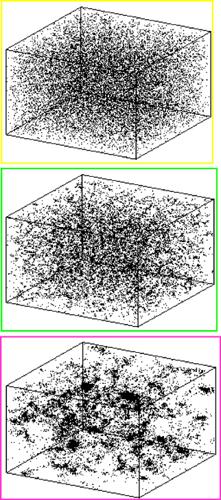
Il modello concettualmente più semplice suggerito da questa problematica è lo studio dell'aggregazione gravitazionale di un insieme di punti massivi, con una distribuzione iniziale casuale e condizioni periodiche al contorno. Il risultato di una simulazione di questo tipo, per una distribuzione di Poisson, è riportato nella fig. 5. Le strutture formate hanno delle similarità con quelle osservate, ma anche molte differenze. La più grave è che non sembra possibile generare strutture così estese come quelle osservate in un tempo realistico. Per superare questo problema si è cercato di introdurre condizioni iniziali particolari, insieme al concetto di materia oscura non barionica ed energia oscura repulsiva. Probabilmente i nuovi dati del progetto SDSS (Sloan digital sky survey), una campagna osservativa in grado di coprire un quarto di cielo e di fornire una mappa tridimensionale di circa un milione di galassie e quasar, offriranno importanti elementi di riflessione.
Dalla fisica alla biologia: strutture complesse evolutive
Una parte della biologia appare come un'affascinante palestra per lo studio dei sistemi complessi autoorganizzati oggetto di ricerca in fisica; rimangono tuttavia alcune specificità all'interno delle due discipline. La fisica cerca di semplificare e idealizzare sistemi e fenomeni, con l'obiettivo di formulare leggi generali; la biologia studia la realtà per come è e le sue domande sono rivolte alle strutture e ai processi degli organismi viventi. In questo senso biologia è una disciplina storica, dipende dalle leggi della fisica ma anche dall'enorme quantità di informazioni che si sono accumulate attraverso il meccanismo specifico dell'evoluzione avvenuta sulla Terra. Una delle caratteristiche principali dell'evoluzione biologica è di apprendere dall'esperienza; dunque, la biologia studia sistemi di tipo adattativo. Il punto cruciale è capire come strutture ben organizzate di tipo adattativo possano emergere spontaneamente dalla dinamica dissipativa di un sistema complesso. L'emergere di organismi viventi ordinati e ben organizzati può sembrare in contrasto con il secondo principio della termodinamica, secondo il quale un sistema evolve sempre verso uno stato con maggiore entropia (disordine); tuttavia questo principio si applica soltanto a sistemi isolati. La Terra è un sistema aperto, in quanto riceve continuamente energia dal Sole: tale flusso energetico produce ordine locale.
bibliografia
Bak 1987: Bak, Per - Tang, Chao - Wiesenfeld, Kurt, Self-organized criticality: an explaination of 1/f noise, "Physics review letters", 59, 1987, pp. 381-384.
Baryshev, Teerikorpi 2002: Baryshev, Yurij - Teerikorpi, Pekku, Discovery of cosmic fractals, Singapore-River Edge (N.J.), World Scientific, 2002.
Caldarelli 2006: Caldarelli, Guido, Scale-free networks, complex webs (www.pil.phys.uniroma1.it/~gcalda/book.html).
Cardy 1996: Cardy, John, Scaling and renormalization in statistical physics, Cambridge, Cambridge University Press, 1996.
Erdös, Rényi 1959: Erdös, Paul - Rényi, Alfred, On random graphs, "Publicationes mathematicae", 6, 1959, pp. 290-297.
Erzan 1995: Erzan, Ayse - Pietronero, Luciano - Vespignani, Alessandro, The fixed scale transformation approach to fractal growth, "Review of modern physics", 67, pp. 545-604.
Evertsz 1996: Fractal geometry and analysis, edited by Carl J.G. Evertsz, Hine-Otto Peitgen, Richard F. Voss, Singapore, World Scientific, 1996.
Gabrielli 2005: Gabrielli, Andrea e altri, Statistical physics for cosmic structures, Berlin-New York, Springer, 2005.
Gell-Mann 1994: Gell-Mann, Murray, The quark and the jaguar: adventures in the simple and the complex, New York, Freeman, 1994.
Huang 1987: Huang, Kerson, Statistical mechanics, 2. ed., New York-Chichester, Wiley, 1987.
Kadanoff 1990: Kadanoff, Leo P., Scaling and universality in statistical physics, "Physica A", 163, 1990, pp. 9-11.
Kadanoff 1993: Kadanoff, Leo P., From order to chaos, Singapore-London, World Scientific, 1993.
Kauffman 1993: Kauffman, Stuart A., The origins of order: self-organization and selection in evolution, New York, Oxford University Press, 1993.
Mandelbrot 1983: Mandelbrot, Benoît, The fractal geometry of nature, New York, Freeman, 1983.
Ong, Bhatt 2001: More is different, edited by N. Phuan Ong, Ravin N. Bhatt, Princeton, Princeton University Press, 2001.
Pastor Satorras, Vespignani 2004: Pastor Satorras, Romualdo - Vespignani, Alessandro, Evolution and structure of the internet: a statistical physics approach, Cambridge, Cambridge University Press, 2004.
Peebles 1993: Peebles, Phillip J.E., Principles of physical cosmology, Princeton, Princeton University Press, 1993.
Pietronero, Tosatti 1986: Fractals in physics, edited by Luciano Pietronero, Elio Tosatti, Amsterdam-New York, North-Holland, 1986.
Vicsek 1992: Vicsek, Tamás, Fractal growth phenomena, 2. ed., Singapore-London, World Scientific, 1992.
Wilson 1983: Wilson, Kenneth G., The renormalization group and critical phenomena, "Review of modern physics", 55, 1983, pp. 583-600.