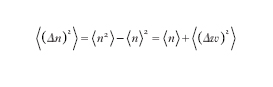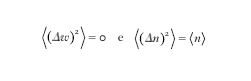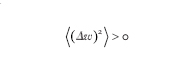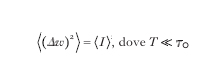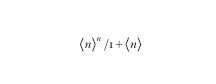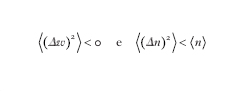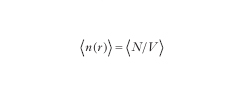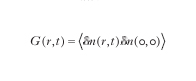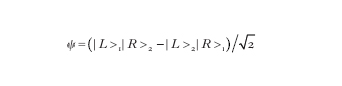COERENZA

Coerenza

Il concetto di coerenza è strettamente legato a quello delle correlazioni esistenti fra variabili che fluttuano statisticamente nel tempo e nello spazio. Inizialmente introdotto per spiegare i fenomeni classici di interferenza, ha poi trovato applicazione in numerosi altri eventi fisici e comincia a trovarne anche in altre discipline. In generale, supponendo di avere una variabile aleatoria associata a un qualunque fenomeno fisico, essa può essere descritta tramite la sua legge di distribuzione, che dà la probabilità che essa assuma un determinato valore in un determinato punto spazio-temporale. Questa legge permette di calcolare il valore medio e la varianza della variabile, grandezze molto spesso già sufficienti a descrivere il fenomeno.

A volte tuttavia non basta conoscere il comportamento statistico della variabile in un determinato punto spazio-temporale, ma è necessario determinare come cambia la variabile quando ci si allontani dal punto considerato. Questa informazione è fornita dalla cosiddetta funzione di correlazione Γ, che, normalizzata al suo valore massimo, varia fra uno e zero.

Nell'intervallo spazio-temporale in cui Γ=1, la grandezza varia nello stesso modo in tutti i punti. Laddove Γ=0 i valori della grandezza variano nei due punti in analisi in modo completamente indipendente. Naturalmente si passa dalla situazione di grandezza le cui fluttuazioni sono completamente correlate a quella in cui le fluttuazioni sono completamente scorrelate (indipendenti una dall'altra) attraverso tutta una serie di valori di Γ intermedi.

Il concetto può essere esteso anche ad altri campi. Nel sistema nervoso centrale la principale attività di un dato gruppo di neuroni è l'interazione con altri gruppi. I gruppi di neuroni (v. neurone) possono interagire fra loro anche a grandi distanze. Un gruppo può modulare la sua velocità di accensione o la sua sincronizzazione di oscillazione interna per influenzare un altro gruppo, e questo si pensa possa essere un meccanismo generale per regolare il flusso di informazione nel sistema nervoso. I gruppi di neuroni attivati oscillano tipicamente in bande di frequenza di poche decine di Hz e quindi possono subire fluttuazioni di eccitabilità temporalmente predicibili. La risposta di un gruppo di neuroni a un altro gruppo eccitatore si ha entro il tempo in cui le oscillazioni dei due gruppi sono fra loro correlate. È in tale direzione che si va muovendo la moderna scienza della comunicazione fra neuroni, usando il concetto di c. fra le loro oscillazioni.

La teoria della c. in ottica, introdotta nella seconda metà del 19° sec. e poi codificata da E. Wolf, è indispensabile per interpretare il formarsi delle frange d'interferenza in un interferometro. Affinché la luce proveniente da sorgenti diverse (per es., i due fori in un'esperienza di Young) possa dar luogo a tale fenomeno, è necessario che le fluttuazioni dei campi elettrici relativi alle due sorgenti siano correlate fra loro, in modo espresso dalla funzione di correlazione, che prende il nome di funzione di correlazione del prim'ordine e consente di determinare il tempo di c. della sorgente (legato alla sua larghezza spettrale) e l'area di coerenza. In un laser (v.) questa correlazione esiste fra tutti i punti della sezione del suo fascio; in una sorgente ordinaria la correlazione esiste solo fra punti che si trovano entro una zona limitata, detta area di coerenza.

Le fluttuazioni del campo elettromagnetico possono anche essere legate a quelle del numero di fotoni, come per primo indicò A. Einstein (1911). Dopo l'introduzione da parte di S.N. Bose ed Einstein (1924) della statistica che regola la radiazione in equilibrio termico, le fluttuazioni della radiazione furono prese in considerazione da diversi studiosi e, negli anni Quaranta del 20° sec., durante la guerra, lo sviluppo e l'applicazione dei rivelatori di radiazione divennero importanti nel campo delle onde radio per determinare il rumore nelle antenne.

Prima del 1950 l'interesse per le fluttuazioni delle radiazioni era largamente basato sulle inevitabili limitazioni che esse imponevano alla precisione delle misure di radiazione. Tra il 1952 e il 1956 R. Hanbury Brown e R.Q. Twiss, lavorando nel campo della radioastronomia, svilupparono una nuova tecnica interferometrica per la determinazione dei diametri angolari delle sorgenti radio in cui la misura delle fluttuazioni di radiazione giocava un nuovo ed essenziale ruolo; più tardi applicarono questa tecnica alle onde luminose (1956-57). Essi mostrarono che il grado di c. fra due punti in un campo di radiazione può essere ricavato dalle misure di correlazione dei segnali fluttuanti misurati in due antenne radio poste nei due punti. Non si misurava più la correlazione fra i valori del campo in due punti diversi, ma la correlazione fra i valori dell'intensità dei fasci luminosi. L'importanza del nuovo metodo è connessa alla circostanza che l'intensità di un'onda, essendo proporzionale al modulo quadrato del campo elettrico, non è influenzata dalle fluttuazioni di fase e quindi la misura delle correlazioni fra le fluttuazioni dell'intensità non è legata alle fluttuazioni di fase che vengono introdotte dalla turbolenza atmosferica. Tali risultati, facilmente accettati in ambito radio, se applicati alla radiazione luminosa e interpretati in termini di fotoni ponevano una serie di questioni.

R. Glauber (premio Nobel 2005 per la fisica per la sua teoria sugli stati coerenti), analizzando da un punto di vista quantistico il problema della c., pose nel 1963 le basi per la nascita dell'ottica quantistica, analizzando la rappresentazione quanto-meccanica nel campo, inquadrando i risultati di Hanbury Brown e Twiss nel giusto contesto e introducendo gli stati coerenti. Tali stati, già presi in considerazione da E. Schrodinger nel 1927 come soluzioni quantistiche dell'oscillatore armonico, furono e sono lo strumento di base per lo sviluppo della teoria quantistica della coerenza. Gli stati quantici sono quelli di minima incertezza e quindi sono adatti per la descrizione dei fenomeni cooperativi bosonici, come la c. ottica. Essi sono gli stati più vicini agli stati classici permessi dalla meccanica quantistica, poiché includono solo le fluttuazioni quantistiche del vuoto.

La trattazione del problema della rivelazione della radiazione su basi puramente quanto-meccaniche porta all'introduzione di una gerarchia di funzioni di correlazioni per il campo in punti spazio-temporali differenti, capaci di rappresentare esperimenti di coincidenza a n-fotoni. La prima di queste funzioni, perfettamente analoga alla funzione del prim'ordine classica, permette di discutere tutti gli esperimenti di c. ottica classica legati all'assorbimento del singolo fotone. La funzione immediatamente superiore, che in termini classici è rappresentata dalla correlazione fra le intensità in due punti spazio-temporali diversi, è legata all'assorbimento di due fotoni e spiega l'esperienza di Hanbury Brown e Twiss. Le altre funzioni di ordine superiore entrano in gioco in esperimenti in cui sono coinvolti più di due fotoni.

Il punto di partenza della trattazione di Glauber è costituito dal fatto che l'intensità di un fascio luminoso è misurata da dispositivi che assorbono fotoni emettendo elettroni per effetto fotoelettrico; quindi, contando i fotoelettroni, si possono determinare le proprietà statistiche del campo luminoso. Mentre gli esperimenti sulla c. del prim'ordine sono incapaci di distinguere fra stati della luce con distribuzioni spettrali identiche, ma con differenti distribuzioni nel numero di fotoni, nell'esperimento di Hanbury Brown e Twiss si considera la coincidenza fra due rivelatori quando uno di essi registra un fotone al tempo t e l'altro uno al tempo t+τ. Se il ritardo di tempo τ è minore del tempo di coerenza τ0 si può avere l'informazione sulla statistica dei fotoni del fascio. Il risultato dell'esperimento è che nel caso della luce di una sorgente ordinaria, per τ=0 si ha un tasso di conteggi doppio che per grandi ritardi, cioè i fotoni arrivano 'addensati' in paia (photon bunching effect) mentre in uno stato coerente (per es., per un laser ben stabilizzato) tale effetto non si presenta.

Questa trattazione quantistica mostra la possibilità dell'esistenza di nuovi campi con proprietà di c. che non trovano alcun analogo in una visione classica. Per apprezzare completamente questo nuovo aspetto della teoria della c. è opportuno considerare le leggi di distribuzione dei fotoni per i vari casi. La varianza del numero di fotoelettroni emessi (fotoni assorbiti se l'efficienza quantica è unitaria) è data dalla formula di Einstein

formula [

1]

dove il primo termine rappresenta la varianza di particelle (fotoni) che seguono la statistica di Poisson e il secondo le fluttuazioni d'onda generalizzate. Per campi coerenti

e cioè la statistica dei fotoni è poissoniana. I campi classici hanno

e sono detti superpoissoniani: per es., per il campo caotico di una sorgente naturale di intensità media ⟨I ⟩ si ha

è il tempo di rivelazione, e  ⟨(Δn)²⟩ = ⟨n ⟩(1+⟨n⟩) che corrisponde alla distribuzione di Bose-Einstein

Per campi quantistici che non hanno analogo classico può aversi

cioè una legge subpoissoniana. Campi puramente quantistici che non hanno analoghi classici possono presentare varie statistiche quantistiche e proprietà di correlazione come l'antibunching dei fotoni, in cui i fotoni tendono a non essere ammassati, una statistica subpoissoniana e lo squeezing (strizzamento) delle fluttuazioni della parte reale o immaginaria dell'ampiezza complessa del campo sotto il livello corrispondente alle fluttuazioni isotrope del vuoto. Glauber applicò la tecnica degli stati coerenti alla descrizione della c. quantica come un fenomeno cooperativo bosonico e, quindi, in tal modo si possono rappresentare anche la superconduttività e gli stati condensati di Bose-Einstein. Nel caso della condensazione di Bose-Einstein si ha l'esistenza di effetti di c. associati con la fase del parametro d'ordine; nel caso dei superfluidi e superconduttori l'effetto di c. è connesso alle interazioni. In un gas ideale classico, descritto completamente dalla sua temperatura e densità, la sola lunghezza caratteristica è la distanza media fra gli atomi o molecole (a temperatura ambiente e pressione atmosferica di circa 3 nm). La meccanica quantistica assegna, invece, una lunghezza di influenza di ogni atomo con il suo vicino:questa è data dalla lunghezza d'onda di de Broglie. Se si raffredda il gas a temperature sotto il milionesimo di kelvin, la lunghezza di de Broglie supera la distanza media fra gli atomi ed emergono correlazioni quantistiche che rendono tutti gli atomi della cella mutuamente vincolati e indistinguibili l'uno dall'altro; essi collassano in un singolo stato quantico chiamato condensato (condensazione di Bose-Einstein). Tale fenomeno ha luogo per tutte le particelle che sono bosoni, cioè a spin nullo o intero. In questo stato condensato è possibile ottenere interferenza e diffrazione tra fasci di atomi e per descrivere i vari fenomeni si applicano i concetti di c. e di stati coerenti usati in ottica. Si può parlare così, per es., anche di stati atomici squeezed.

Nel caso di fermioni (particelle con spin semiintero) non è possibile definire stati coerenti come quelli ottici a causa del principio di esclusione di Pauli, ma è possibile comunque svolgere considerazioni sull'esistenza di correlazioni nei parametri che descrivono le funzioni d'onda. Così, per es., la c. delle onde elettroniche può essere distrutta da processi di diffusione degli elettroni. Definendo una lunghezza di coerenza di fase (Λφ), che è possibile legare alla diffusività, e una lunghezza termica (ΛT) legata all'allargamento termico dei livelli d'energia degli elettroni, analoga alla lunghezza di c. della luce, se ΛT>Λφ il processo di diffusione anelastico è quello dominante nel distruggere la c. delle onde elettroniche. Analoghe considerazioni valgono per il campo fononico. L'importanza delle correlazioni può anche essere vista, nella forma più generale, considerando un qualunque mezzo materiale. La maggior parte dei sistemi in natura hanno interazioni su brevi distanze che possono produrre fenomeni cooperativi. Consideriamo un fluido confinato in un volume contenente N particelle. Le proprietà microscopiche possono essere descritte da una densità di probabilità di trovare le particelle in certe posizioni con certi valori della quantità di moto. La densità in un determinato punto n(r) è quindi una grandezza fluttuante di cui si può calcolare il valore medio in termini della precedente probabilità. In un sistema uniforme esso è indipendente dalla posizione e vale

Se consideriamo le fluttuazioni δn (r, t) = n(r, t) - ⟨n⟩ è possibile analizzare la funzione di correlazione dipendente dal tempo

In un fluido la funzione di correlazione densità è legata alla compressibilità isoterma e determina l'intensità della luce diffusa ed è fondamentale per descrivere le fluttuazioni nelle transizioni di fase e nei fenomeni critici.

Accenniamo, infine, al problema della sovrapposizione degli stati in meccanica quantistica e alla cosiddetta decoerenza degli stati. Einstein, Podolsky e Rosen (EPR) nel 1935 esaminarono le conclusioni a cui porta la meccanica quantistica per due particelle che abbiano interagito fra loro. In particolare, nel ragionamento di Einstein le particelle mostrerebbero correlazioni che sarebbero in contraddizione con il principio di indeterminazione di Heisenberg. E. Schrodinger nello stesso anno, in risposta alle osservazioni di EPR, introdusse la nozione di entanglement "ingarbugliamento" per descrivere tali correlazioni quantistiche, osservando che due particelle entangled devono essere viste come un tutt'uno e non come due entità separate. Recentemente, l'entanglement è stato osservato in diversi casi e si è mostrato che esso scompare a causa dell'interazione con il mondo esterno (decoerenza), per cui può essere visto come una proprietà di c. delle funzioni d'onda associate alle due particelle.

Per es., due fotoni possono essere entangled quando sono emessi in rapida successione da un atomo eccitato: se sono emessi quando l'elettrone decade in due transizioni successive a un livello inferiore e se gli stati iniziale e finale hanno entrambi momento angolare orbitale zero. In questo caso, se il primo fotone è, per es., polarizzato circolare sinistro e ha uno stato quantico ∣L⟩₁,allora il secondo fotone deve essere polarizzato circolare destro e avere uno stato quantico ∣R⟩₂ e viceversa. La funzione d'onda che descrive il fenomeno è la sovrapposizione coerente

formula [

2]

dove il segno meno riflette il fatto che lo stato finale ha spin zero. La funzione d'onda non è più il prodotto degli stati quantici dei due fotoni separatamente, ma una combinazione che può però essere distrutta dall'interazione con il mondo esterno annullando la c. dello stato. Nel caso in cui i due fotoni vengano lasciati viaggiare in due direzioni diverse, senza subire interazioni che possano distruggere lo stato anche quando siano separati da una grande distanza uno dall'altro, se misurandone uno lo si trova polarizzato circolare destro, l'altro deve essere polarizzato sinistro. L'essenza della [2] è tuttavia che entrambi i fotoni sono in una sovrapposizione dei due stati, fintantoché uno di essi non sia misurato. Il processo di misura è tale che fa collassare lo stato di uno dei due in una delle due polarizzazioni e automaticamente l'altro, a grandissima distanza dal primo, viene a trovarsi nell'altra polarizzazione.

Tale paradosso indusse Einstein a dichiarare che la meccanica quantistica non è una teoria completa. Tralasciando tale questione, numerosi esperimenti hanno mostrato che, qualora la sovrapposizione dei due stati resti coerente, si ha esattamente il comportamento che è stato descritto sopra.

Il problema di mantenere la c. della sovrapposizione è essenziale nello sviluppo dei computer quantistici.

bibliografia

M. Born, E. Wolf, Principles of optics, Oxford 1980, Cambridge 1997⁶; L. Mandel, E. Wolf, Optical coherence and quantum optics, Cambridge 1995.