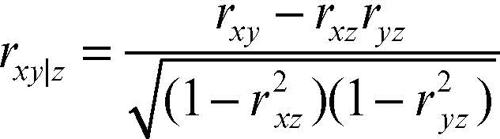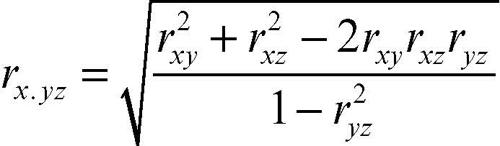correlazione, coefficiente di
correlazione, coefficiente di
correlazione, coefficiente di detto anche indice di correlazione lineare o indice di Bravais-Pearson, coefficiente che misura l’intensità della correlazione tra due variabili aleatorie o due caratteri statistici quantitativi X e Y, relativi alla stessa popolazione. È così calcolato:
dove σxy è la covarianza delle due variabili e σxσy è il prodotto dei loro scarti quadratici medi.
Il coefficiente di correlazione lineare varia da −1 a +1 (estremi compresi) e, in particolare:
• se r > 0 si parla di correlazione positiva, e se r è prossimo a 1 a valori “grandi” del primo carattere tendono a essere associati valori “grandi” del secondo carattere;
• se r < 0 si parla di correlazione negativa, e se r è prossimo a −1 a valori “grandi” del primo carattere tendono a essere associati valori “piccoli” del secondo carattere.
Se tale valore è vicino a ±1 si può dunque dire che tali caratteri sono associati o correlati: ciò non significa necessariamente che siano l’uno la causa dell’altro, perché potrebbe per esempio verificarsi che essi abbiano una concausa comune, ma nessuno dei due sia causa diretta dell’altro, oppure anche che non ci sia alcun legame logico.
Quando r è uguale a ±1, le due variabili X e Y sono dipendenti secondo una legge lineare. Poiché il coefficiente di correlazione è simmetrico rispetto alle due variabili, è necessario scegliere quale delle due variabili vada considerata dipendente rispetto all’altra. Se si considera Y come variabile dipendente, allora la legge lineare è del tipo Y = aX + b, dove a è positivo se r = 1, negativo se r = −1 (correlazione lineare perfetta). In caso di indipendenza lineare tra X e Y allora r = 0 e si dirà che vi è assenza di correlazione. Non è però vero il viceversa: se infatti r = 0 si può soltanto affermare che la covarianza di X e Y è nulla, ma ciò non assicura che le due variabili siano indipendenti; potrebbero per esempio essere correlate non linearmente, ma secondo una legge quadratica. Inoltre, a rigore, il coefficiente di correlazione è applicabile quando le due variabili hanno una distribuzione normale o, almeno, simmetrica e unimodale. Pertanto, per piccoli campioni, per i quali non si possono fare ipotesi di distribuzione parametrica standard, si utilizzano altri indicatori di correlazione, quali per esempio il coefficiente di → correlazione per ranghi.
Il coefficiente di correlazione è indipendente da trasformazioni lineari delle variabili e quindi rimane uguale se, anziché le variabili X e Y, si considerano variabili aX + b e cY +d (con a e c maggiori di 0); esso non dipende perciò dalle unità di misura utilizzate e, per esempio, il valore trovato fra temperatura ambientale e lunghezza di una sbarra è indipendente dal fatto che si misurino la temperatura in gradi Celsius o in gradi Fahrenheit e la lunghezza in metri o in pollici.
Coefficiente di correlazione parziale (o netta)
In alcune situazioni, la correlazione tra due variabili X e Y é influenzata dalla presenza di altre variabili. Per esempio, il peso e l’altezza di un gruppo di studenti, tra loro correlati, potrebbero essere a loro volta correlati alla loro età. Si costruisce perciò un coefficiente di correlazione parziale che consente di eliminare l’effetto di tale terza variabile (e la parzializzazione può agevolmente essere applicata a ulteriori variabili). Perciò, date tre variabili X, Y e Z, la correlazione tra X e Y viene tarata eliminando la correlazione fra X e Z e fra Y e Z e quindi considerando costante Z:
Nella formula rxy, rxz, ryz sono i coefficienti di correlazione lineare relativi, rispettivamente, alle coppie di variabili X e Y, X e Z e Y e Z.
Si può osservare che:
• se X e Y non sono correlate con Z, allora rxy|z = rxy, cioè il coefficiente di correlazione parziale coincide con il coefficiente di correlazione tra X e Y;
• se la correlazione di X o Y con Z è perfetta (e quindi rxz = ±1 oppure ryz = ±1), il denominatore si annulla e il coefficiente di correlazione parziale non è calcolabile.
Coefficiente di correlazione multipla
In alcune situazioni, date tre variabili X, Y, Z, la prima può essere considerata dipendente dalle altre due considerate come esplicatori simultanei. Per esempio la domanda di un determinato prodotto può essere correlata sia con il suo prezzo sia con il livello del reddito nazionale. Nell’ipotesi che le variabili siano correlate linearmente a due a due, il coefficiente di correlazione multipla è:
Nella formula i singoli valori di r sono relativi alle coppie di variabili indicate a pedice.