Ippia, trisettrice di
Ippia, trisettrice di
Ippia, trisettrice di detta anche quadratrice di Ippia o di Dinostrato, curva piana trascendente, di equazione cartesiana
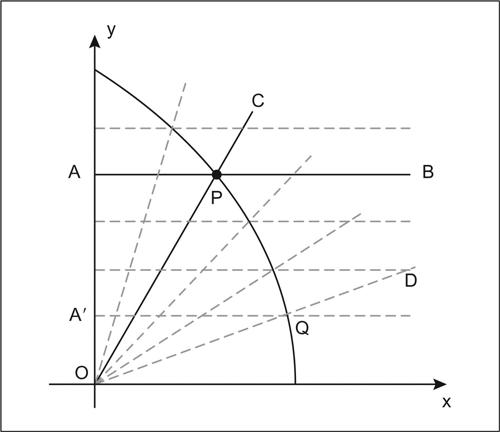
ottenuta come luogo dei punti di intersezione tra due segmenti di uguale lunghezza, che si muovono contemporaneamente, uno di moto rettilineo uniforme, parallelamente a sé stesso, l’altro di moto circolare uniforme intorno a un suo estremo. Nella figura, la trisettrice è descritta dal punto P, al variare delle posizioni dei segmenti AB e OC. Tale curva fu utilizzata da Ippia di Elea per la trisezione dell’angolo: per suddividere l’angolo DÔC (in figura) in tre angoli di uguale ampiezza si considerano i punti P e Q in cui OC e OD intersecano la trisettrice e le loro rispettive proiezioni A e A′ sull’asse y; dividendo in tre segmenti di uguale lunghezza il segmento AA′ e considerando i rispettivi punti sulla trisettrice si ottengono i tre angoli cercati. La curva fu successivamente usata da Dinostrato per la quadratura del cerchio (→ quadratura), da cui il nome di quadratrice.