trigonometria

trigonometria

Settore della matematica che, come spiega la radice greca del nome (trigonon «triangolo» e metron «misura»), analizza le relazioni fra gli elementi (angoli e lati) di un triangolo, basandosi sulle funzioni trigonometriche (seno, coseno, tangente e cotangente di un angolo).

Misura degli angoli

La misura di un qualsiasi angolo (e in particolare di quelli di un triangolo) può essere espressa in gradi o in radianti. Un grado è la 360^a parte dell’angolo giro ed è a sua volta suddiviso in primi (un sessantesimo di grado) e in secondi (un sessantesimo di primo). L’angolo piatto, metà del giro, ha dunque 180° e quello retto, un quarto del giro, 90° e in generale un angolo che misuri un n-esimo dell’angolo giro misura 360/n gradi.

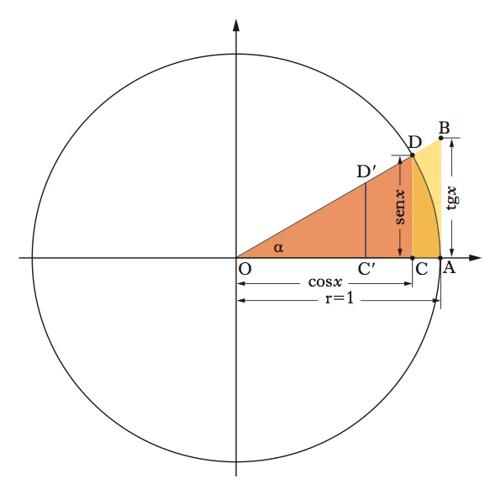
Meno nota, ma più maneggevole matematicamente la misura in radianti. Si consideri una retta orizzontale e, data un’unità di misura, si scelgano due punti su tale retta, O e A (alla destra di O, figura); sia r=1 la misura del segmento che congiunge i due punti; si costruisca ora una circonferenza con centro in O e raggio unitario e si immagini di percorrerla, partendo da A, in senso antiorario fino a un punto D tale che l’angolo α formato dai segmenti OA e OD sia inferiore a 180°. Ricordando che la lunghezza della circonferenza di raggio 1 è 2π, risulta che il rapporto fra la lunghezza x del cammino OD lungo la circonferenza e quella 2π della circonferenza è pari al rapporto α/360. Quindi x=2πα/360. Il puro numero x così definito è la misura in radianti dell’angolo la cui misura in gradi è α. Per es., la misura in radianti dell’angolo di 90° è x=π/2, quella dell’angolo di 45° è x=π/4, mentre è 1 la misura in radianti dell’angolo di 180/π°, circa 57°, 17 primi 20 secondi.

Funzioni trigonometriche

Indicando con C il punto ottenuto proiettando perpendicolarmente D sulla retta orizzontale si definiscono le seguenti funzioni trigonometriche: sinx (leggi seno di x)=lunghezza con segno del segmento DC (positiva se 0<x<π, negativa se π<x<2π, nulla se x=0, π, 2π); cosx (leggi coseno di x) = lunghezza con segno del segmento OC (positiva se 0<x<π/2, negativa se π/2<x<3π/2, di nuovo positiva se 3π/2<x<=2π, nulla se x=π/2, 3π/2); tgx (tangente di x)=senx/cosx (definita dove cosx diverso da 0); cotgx (cotangente di x)= cosx/senx=1/tgx.

Risoluzione dei triangoli rettangoli

Fissato l’angolo di misura α in gradi e x, supposto compreso fra 0 e π/2 in radianti, si costruisca il triangolo rettangolo OD′C′ scegliendo liberamente un punto D′ sul segmento OD e C′ dalla proiezione di D′ su OA. Si indichi con a,b,c, rispettivamente le lunghezze dell’ipotenusa, del cateto altezza e del cateto base del triangolo rettangolo D′OC′. I triangoli rettangoli DOC e D′OC′ sono simili e vale allora la OD′/OD=OC′/OC. Tenendo conto che OD =1 perché raggio della circonferenza e OC=cosx si ha: a=c/cosx ovvero c=a cosx. Vale quindi la regola che in un triangolo rettangolo un cateto è uguale al prodotto dell’ipotenusa per il coseno dell’angolo adiacente (formato dal cateto e dall’ipotenusa). Sempre per la similitudine deve valere anche la OD′/OD=D′C′/DC cioè a=b/senx, da cui b=a senx, per cui un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto (formato dall’altro cateto e dall’ipotenusa).

Per calcolare l’area di un triangolo del quale si conoscono la lunghezza della base b, quella a di uno degli altri due lati e il seno dell’angolo γ formato da tale lato e dalla base, si sfrutta il fatto che l’altezza h del triangolo è interpretabile come cateto del triangolo rettangolo di cui il lato di lunghezza a è ipotenusa; risulta dunque h=a senγ e quindi per banale applicazione della formula dell’area S di un triangolo S=bh/2=b a senγ/2.