Tartaglia, triangolo di

Tartaglia, triangolo di

Triangolo indefinito composto da numeri interi disposti secondo righe orizzontali di lunghezza crescente, noto sin dall’anno 1000 ai cinesi e ai persiani; in Europa il primo a studiarne le proprietà sembra sia stato l’algebrista bresciano N. Fontana, detto appunto Tartaglia per la sua balbuzie, anche se in molti Paesi il triangolo è associato al nome di B. Pascal.

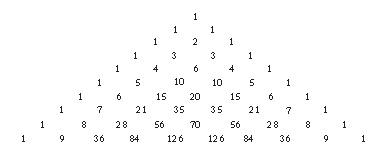
Al variare di n sui numeri naturali si possono considerare triangoli composti da n righe (v. fig.); la generica riga r-esima contiene esattamente r elementi (la prima riga un solo elemento, la seconda 2, la terza 3 e così via). Indichiamo con la notazione x(r,s) l’elemento s-esimo della riga r. Primo e ultimo elemento di ogni riga sono pari a 1; formalmente x(r,1)=x(r,r)=1 per ogni r. Per ogni s=2,…,r−1, gli elementi interni del triangolo soddisfano poi la x(r,s)=x(r−1,s−1)+x(r−1,s). Tale proprietà è suscettibile di interessanti interpretazioni collegate allo sviluppo del binomio (a+b)^r=Σ_s=0,…,r C_r,s a^r−sb^s, versione generale delle ben note formule del quadrato (a+b)²=a²+2ab+b², e del cubo di un binomio (a+b)³=a³+3a²b+3ab²+b³. Risulta infatti che la sequenza ordinata (a partire da s=0 e fino a r) dei coefficienti C_r,s della potenza r-esima (a+b)^r del binomio,  corrisponde agli elementi della r+1-esima riga del triangolo. Per es. i 4 coefficienti 1,3,3,1 dello sviluppo di (a+b)³ (quindi con r=3) corrispondono ai 4 elementi della quarta riga del triangolo. Per tale motivo essi sono detti coefficienti binomiali (dello sviluppo del binomio); il loro significato combinatorio è quello di numero dei modi in cui si possono scegliere s elementi da un gruppo di r. Per es. il coefficiente 3 del termine a²b indica che vi sono 3 modi di scegliere due volte a e una volta b (così da ottenere a²b come prodotto): a-a-b (a primo e secondo) oppure a-b-a (a primo e terzo) oppure b-a-a (a secondo e terzo). Il valore dei coefficienti binomiali è descritto dalla C_r,s=r!/s!(r−s)! valida per ogni 0≤s≤r, ove h!=h∙(h−1)∙…∙2∙1 cioè h! è il prodotto dei primi h numeri interi e con la convenzione che 0!=1. Sempre nell’esempio C_3,2 =3!/2!(3−2)!= 3∙2∙1/2∙1∙1=3 come abbiamo visto. Ponendo a=b=1 si ha poi (a+b)^r=(1+1)^r=2^r =Σ_s=0,…,r C_r,s e risulta che la somma degli elementi del­la riga r+1-esima del triangolo è (per ogni r) 2^r.