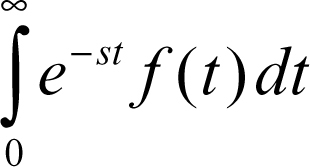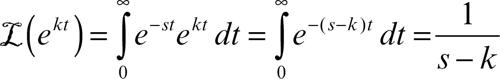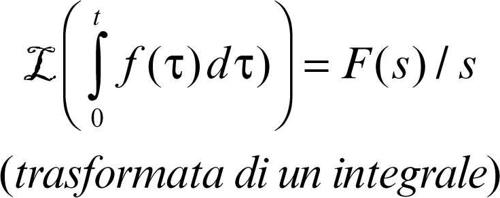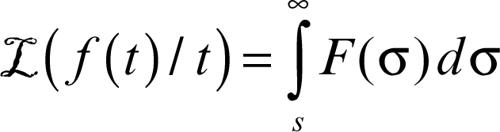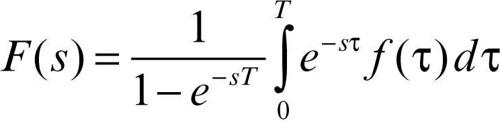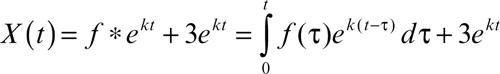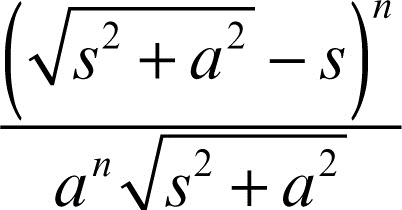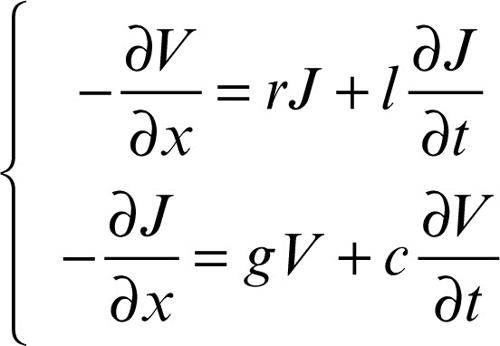Laplace, trasformazione di
Laplace, trasformazione di
Laplace, trasformazione di utile strumento per lo studio di equazioni differenziali lineari, sia ordinarie che alle derivate parziali, perché permette di trasformare problemi differenziali in problemi algebrici, riducendone così la difficoltà e trasformandone la soluzione in un calcolo simbolico.
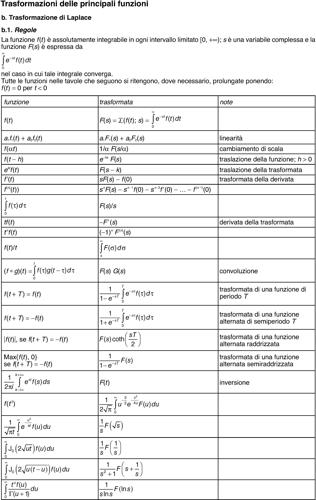
Si consideri una funzione ƒ(t) assolutamente integrabile in ogni intervallo limitato di [0, +∞), e sia s una variabile complessa. Se per qualche valore di s l’integrale
converge, esso risulta una funzione F(s) che si chiama trasformata (unilatera) di Laplace di ƒ(t). Tale funzione si designa spesso col simbolo F(s) = ℒ(ƒ(t), s) o semplicemente ℒ(ƒ(t)) dove ℒ indica la trasformazione di Laplace. Si dimostra che F(s) risulta una funzione analitica della variabile complessa s, olomorfa nel dominio {Re(s) > λ} ⊆ C, detto semipiano di convergenza della trasformata; λ è detta ascissa di convergenza.
In alcune questioni è importante considerare l’assoluta convergenza dell’integrale, che si ha in un semipiano {Re(s) > μ}, dove μ ≥ λ è l’ascissa di assoluta convergenza. È possibile che sia λ = −∞, come nel caso di
la scrittura λ = +∞ indica invece che ƒ(t) non è trasformabile, come per esempio la funzione ƒ(t) = e(t2). La conoscenza di F(s) per s reale basta a individuare F(s) anche nel campo complesso, per cui sovente si considera s ∈ R; anche il valore dell’ascissa di convergenza è irrilevante nelle applicazioni più comuni. La trasformazione può essere considerata come un particolare operatore che associa, nelle condizioni indicate, alla funzione ƒ(t) a valori reali (considerata spesso come funzione del tempo) una funzione nella variabile complessa F(s). Si noti che, essendo l’integrale calcolato sull’intervallo [0, +∞), i valori eventualmente assunti da ƒ(t) per t < 0 non hanno interesse (in ciò confermando del resto l’interpretazione della variabile t come tempo). Anzi, se si vuole pensare la trasformata come un caso particolare della trasformata bilatera
si deve ritenere ƒ(t) prolungata con 0 per t < 0, o, se si preferisce, moltiplicata per la funzione di Heaviside Y(t). La trasformata bilatera converge (assolutamente) in una striscia di (assoluta) convergenza, λ′ ≤ μ′ < Re(s) < μ″ ≤ λ″, ma ha impieghi molto meno significativi. Essa è tuttavia richiesta per la scrittura della formula generale dell’antitrasformazione di → Laplace.
Le più semplici trasformate si calcolano direttamente. Si ottiene così per esempio la trasformata
(con k ∈ C; λ = Re(k)), e per k = 1 si ha
in particolare ℒ(1) = 1/s.
Per funzioni più complicate si utilizzano le proprietà delle trasformate:
• linearità: ℒ(a1ƒ1(t) + a2ƒ2(t), s) = a1ℒ(ƒ1(t)) + a2ℒ(ƒ2(t)) = a1F1(s) + a2F2(s). Da questa proprietà si ricava che la trasformata di Laplace prodotto di una funzione per una costante si ottiene moltiplicando per tale costante la trasformata della funzione e che la trasformata di Laplace di una somma di funzioni si ottiene sommando le rispettive trasformate delle singole funzioni. Come applicazione si ricavano le seguenti trasformate:
e
Infatti, tali espressioni si ricavano applicando le formule di Eulero che permettono di scrivere
e utilizzando la proprietà di linearità a partire dalla trasformata di funzioni del tipo ekt;
• cambiamento di scala: ℒ(ƒ(αt)) = (1/α) F(s/α);
• traslazione della variabile t: ℒ(ƒ(t − h)) =e−hs F(s), valida solo per una generica costante h > 0; si noti che ƒ(t) vale 0 per t < 0 e quindi ƒ(t − h) = 0 per 0 ≤ t < h. Inoltre se ƒ(t) è una funzione ℒ-trasformabile e F(s) è la sua trasformata, allora si può scrivere ℒ(ektƒ(t)) = F(s – k), dove k è una generica costante (traslazione della variabile s);
• trasformata di una derivata: ℒ(ƒ′ (t)) = sℒƒ(t)) + − F(0) = sF(s) – ƒ(0). Questa proprietà richiede l’ipotesi che ƒ(t) sia assolutamente continua e ƒ′ (t) sia trasformabile. La sua generalizzazione porta a ottenere l’uguaglianza ℒ(ƒ″ (t)) = s2F(s) – sƒ(0) – ƒ′ (0) e genericamente, sempre nell’ipotesi che tali derivate siano trasformabili, ℒ(ƒ(n)(t)) = snF(s) − sn−1ƒ(0) − sn−2ƒ′ (0) − … −ƒ(n−1)(0), ma anche
• prodotto per la variabile t: ℒ(tƒ(t)) = − dℒ(ƒ(t))/ds = −F′ (s). Questa formula è sempre lecita perché F(s), in quanto analitica nel semipiano di convergenza, possiede derivate di ogni ordine (e l’ascissa di convergenza rimane invariata). Generalizzando si ottiene ℒ(tnƒ(t)) = (−1)nF(n)(s), ma si ottiene anche, se ƒ(t)/t è trasformabile (il che implica f(0) = 0),
In particolare, da
si deduce
• incidenza del periodo: se ƒ(t) ha periodo T, risulta
Definita la convoluzione tra due funzioni ƒ(t) e g(t) come
vale inoltre il teorema della convoluzione, per cui ℒ((ƒ ∗ g)(t)) = F(s)G(s), analogamente a quanto avviene per la trasformata di Fourier (→ convoluzione). Questo risultato è particolarmente utile nelle applicazioni. Per esempio, se si deve risolvere il problema di Cauchy X(0) = 3 per l’equazione differenziale lineare a coefficienti costanti X′ + kX = ƒ(t), trasformando entrambi i membri si otterrà sx(s) − 3 + kx(s) = F(s), da cui x(s) = (F(s) + 3)/(s + k). Si noti che le condizioni iniziali sono inglobate nell’equazione per x(s), in virtù delle formule di trasformazione delle derivate. Ne segue
Nel caso in cui ƒ(t) sia un polinomio o una funzione esponenziale o trigonometrica, si può valutare direttamente la x(t) mediante calcoli algebrici, in quanto la trasformata risulta una funzione razionale: per esempio, per ƒ(t) = t, si ha
e quindi
Se i poli di X(s) sono tutti semplici, si può usare la formula di → Heaviside. Il metodo si può applicare a equazioni o sistemi di equazioni lineari a coefficienti costanti, che vengono ridotti in ogni caso a un’equazione o sistema di primo grado. Pur non essendoci un aumento di potenza rispetto alle formule risolutive per tali equazioni o sistemi, la semplicità di applicazione e la immediata leggibilità delle proprietà della soluzione (ancor prima della trasformazione inversa) rende il metodo della trasformata di Laplace assai vantaggioso.
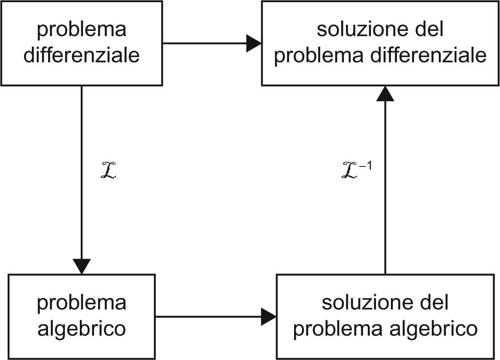
Il ricorso alla trasformazione di Laplace consente quindi di trasformare un problema differenziale in un problema algebrico e, trovata la soluzione di quest’ultimo, tornare al problema di partenza:
Il metodo si può applicare anche a equazioni lineari a coefficienti polinomiali: per esempio, trasformando l’equazione di → Bessel si ottiene la trasformata di Jn(at), che è
Nel caso di equazioni differenziali alle derivate parziali lineari a coefficienti costanti, il metodo della trasformata di Laplace consente di eliminare la dipendenza differenziale dalla variabile temporale t, sostituendola con una dipendenza algebrica, e quindi riduce la complessità dell’equazione che, nel caso di una sola variabile spaziale x, si riduce a un’equazione ordinaria. Tipiche sono le applicazioni allo studio della trasmissione elettrica in una linea a costanti distribuite. Dette V(x, t) e J(x, t) la tensione e la corrente lungo la linea, esse soddisfano il sistema
dove r, l, g, c rappresentano rispettivamente la resistenza, l’induttanza, la conduttanza e la capacità per unità di lunghezza della linea. Eliminando J si ottiene l’equazione dei → telegrafi
(una identica in J si ottiene eliminando V). L’equazione si riduce a quella della corda vibrante per r = g = 0 (linea non dissipativa) e a quella del calore nel caso l = g = 0 (cavo non induttivo). Trasformando tale equazione, nell’ipotesi di linea inizialmente in quiete, si ottiene l’equazione differenziale ordinaria ν″ = (r + ls)(g + cs)ν nell’incognita trasformata ν(x, s), che ha l’integrale generale ν(x, s) = Aekx + Be−kx, dove
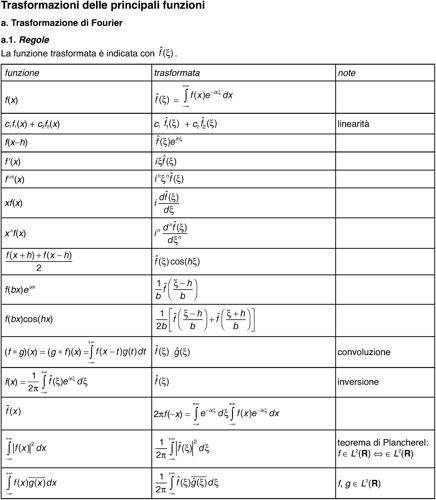
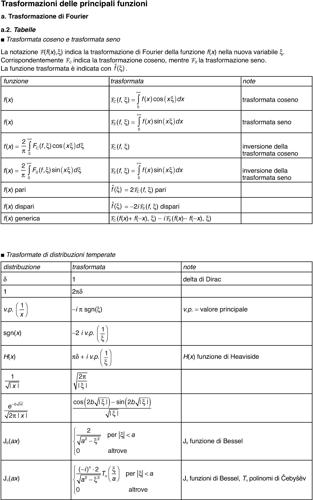
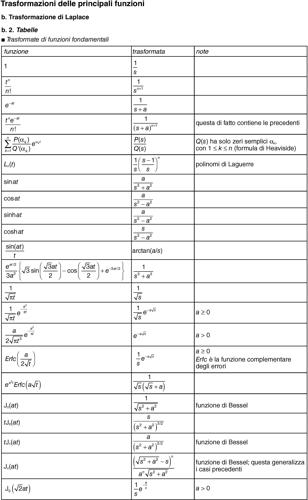
La determinazione delle costanti si esegue imponendo le condizioni ai limiti per la linea (cioè la tensione alle estremità); l’inversione della trasformata, pur con calcoli piuttosto laboriosi, può essere eseguita analiticamente in un gran numero di casi significativi. Si vedano le tavole delle trasformazioni delle principali funzioni.