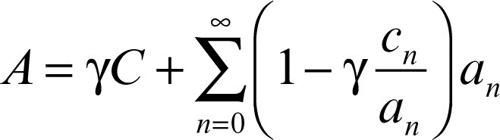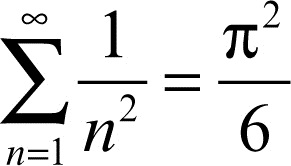Kummer, trasformazione di
Kummer, trasformazione di
Kummer, trasformazione di semplice tecnica per accelerare la convergenza di serie. Se
sono due serie convergenti alle somme A e C rispettivamente e se il rapporto an/cn ammette limite finito γ ≠ 0 per n → ∞, risulta
Se C è noto, il calcolo di A si riduce in questo modo a quello di una serie i cui termini sono infinitesimi di ordine superiore a quelli della serie originaria
Per esempio, se
(è la serie di → Mengoli), si ha γ = 1, C = 1 e il calcolo della serie
si riduce a quello di
Poiché
questo risultato si generalizza a
Se si volesse, per esempio, ottenere un valore approssimato di π2/6 con 6 cifre decimali, con la serie originaria sarebbe necessario un milione di termini, mentre con la seconda, ottenuta attraverso la trasformazione di Kummer, soltanto 708.