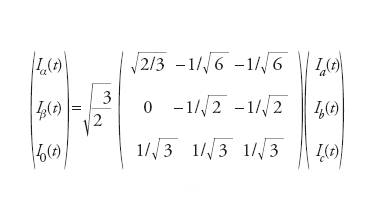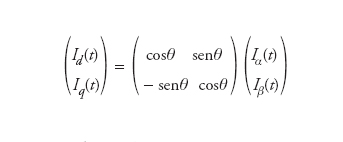trasformata di Park
trasformata di Park
Si considerino tre avvolgimenti a,b,c posti sullo stesso piano ma sfasati spazialmente di 120°, percorsi rispettivamente da correnti sinusoidali con periodo ω ed elettricamente sfasate di 120°. Le tre correnti possono essere rappresentate sul piano dei vettori complessi con una terna di vettori rotanti a velocità ω. È possibile scomporre l’effetto delle tre correnti ia(t), ib(t), ic(t) lungo due assi α e β sfasati fra loro di 90° e posti sullo stesso piano di a,b,c, ottenendo così due correnti iα(t) e iβ(t). Poiché le correnti di fase originali sono tre, affinché la trasformazione sia reversibile, cioè la matrice di trasformazione sia invertibile è necessario considerare un terzo asse ortogonale al piano individuato dagli assi a,b,c e percorso dalla corrente i0(t). Vi è inoltre la necessità di definire i0(t) in modo da rendere tale trasformazione univoca. La prima possibilità è quella che tale trasformazione sia ortogonale a meno di un coefficiente e si dimostra che tale trasformazione è anche tale da mantenere la potenza costante nelle due rappresentazioni.
Per eliminare la dipendenza dalla variabile t, dovrà essere effettuata una seconda trasformazione passando da un riferimento fisso nello spazio a un riferimento rotante alla velocità di rotazione ω, con θ=ωt angolo tra la direzione della corrente della fase a e l’asse d, ossia
Si avrà così una seconda trasformazione dagli assi α e β agli assi d e q. La trasformazione di Park è data quindi dall’insieme delle due trasformazioni dagli assi a,b,c agli assi α, β e 0 e da questi agli assi d,q e 0. Tale trasformazione venne utilizzata già a metà del XX sec. per lo studio della dinamica delle macchine elettriche e successivamente impiegata per il cosiddetto controllo vettoriale degli azionamenti elettrici con macchine asincrone. Nei primi anni di questo secolo fu anche impiegata per il controllo degli inverter trifasi. In questo caso la trasformazione non è più ortogonale e la grandezza invariante scelta non è la potenza ma la lunghezza del vettore corrente ia(t), (rotante sul piano determinato da α e β), scelta uguale al valore massimo della grandezza sinusoidale impiegata. Le equazioni sono analoghe a quelle sopra scritte l’unica differenza è nel coefficiente, posto esternamente alla matrice di trasformazione, che vale 2/3 e non √3/2.